
Комплексные числа - копия
.doc1. Комплексные числа
2.Алгебраическая форма комплексного числа
3.Комплексно-сопряжённые числа
4.Тригонометрическая форма комплексного числа
5.Модуль и аргумент
6.Операции с комплексными числами (сложение, умножение, деление, возведение в степень, извлечение корня).
Комплексные числа представляют собой расширение множества рациональных чисел
Комплексное число
![]() задается двумя действительными числами
a и b.
Эта пара (a,b)
действительных чисел с заданными
определенным образом операциями
умножения и сложения.
задается двумя действительными числами
a и b.
Эта пара (a,b)
действительных чисел с заданными
определенным образом операциями
умножения и сложения.
Комплексное число
![]() записывают
в алгебраической форме как
записывают
в алгебраической форме как
![]() ,
где число
,
где число
![]() называется
мнимой единицей, имеющей свойство
называется
мнимой единицей, имеющей свойство
![]() ,
число a называется
действительной частью числа z,
а число b – мнимой
частью числа z. Их
обозначают Re z
и Im z
соответственно: a =
Re z,
b = Im
z.
,
число a называется
действительной частью числа z,
а число b – мнимой
частью числа z. Их
обозначают Re z
и Im z
соответственно: a =
Re z,
b = Im
z.
Для отображения комплексных чисел используется числовая плоскость, называемая комплексной плоскостью. Можно считать пару чисел (a,b) декартовыми координатам, и тогда получится естественное соответствие комплексных чисел и точек на плоскости.
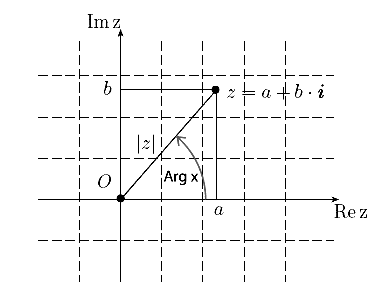
Операции сложения и умножения комплексных
чисел осуществляются так, как если бы
мнимая единица i была
переменной (а комплексные числа —
многочленами от этой переменной), при
этом
![]() .
.
Число z называется
чисто мнимым, если Re
z = 0, например i,
-4i,![]()
Число z называется
действительным (вещественным), если Im
z = 0, например ½,
0,
![]()
Алгебраическая форма.
Запись комплексного числа z в виде
x + iy,![]() , называется алгебраической формой
комплексного числа.
, называется алгебраической формой
комплексного числа.
Сопряженные числа. Если комплексное
число
![]() ,
то число
,
то число
![]() называется комплексно-сопряженным
или просто сопряженным к числу z.
Комплексное число z
и комплексно-сопряженное к нему число
называется комплексно-сопряженным
или просто сопряженным к числу z.
Комплексное число z
и комплексно-сопряженное к нему число
![]() отличаются
знаком мнимой части, действительная
часть у них одинаковая:
отличаются
знаком мнимой части, действительная
часть у них одинаковая:
![]()
-
 (сопряжённое
к сопряжённому есть исходное).
(сопряжённое
к сопряжённому есть исходное).
![]()
Тригонометрическая и показательная формы.
Если вещественную x и мнимую y части комплексного числа выразить через модуль r = | z | и аргумент (x = rcos φ, y = rsin φ), то всякое комплексное число z, кроме нуля, можно записать в тригонометрической форме z = r(cos φ + isin φ).
Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера: z = reiφ, где eiφ — расширение экспоненты для случая комплексного показателя степени.
Отсюда вытекают следующие широко используемые равенства:
![]()
Модуль и аргумент.
Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (расстояние между точкой комплексной плоскости, соответствующей этому числу, и началом координат).
Модуль комплексного числа z
обозначается |z| и определяется
выражением
![]() .
Часто обозначается буквами r
или p. Если z
является вещественным числом, то |z|
совпадает с абсолютной величиной этого
вещественного числа.
.
Часто обозначается буквами r
или p. Если z
является вещественным числом, то |z|
совпадает с абсолютной величиной этого
вещественного числа.
Для любых
![]() имеют
место следующие свойства модуля:
имеют
место следующие свойства модуля:
-
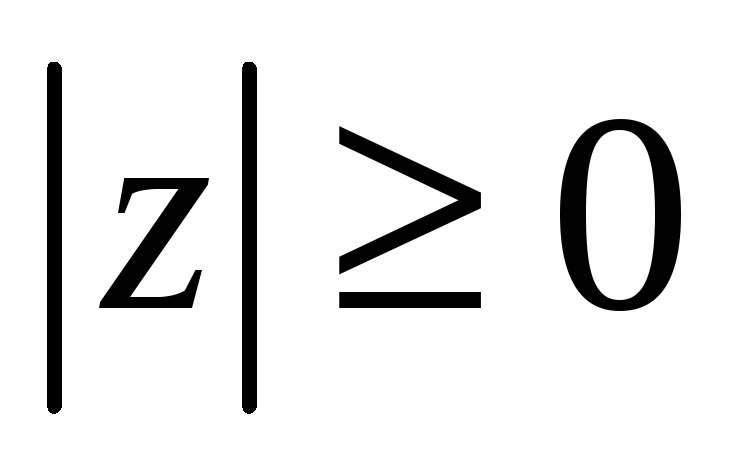 ,
причем
,
причем
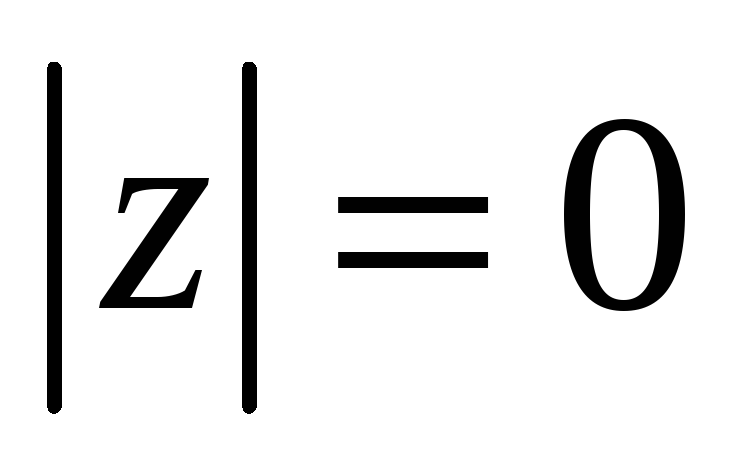 тогда и только тогда, когда z
= 0;
тогда и только тогда, когда z
= 0; -
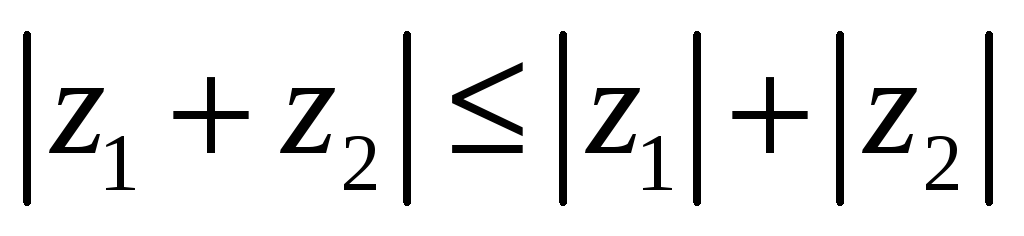 (неравенство
треугольника);
(неравенство
треугольника); -

-

Из третьего свойства следует
![]() ,
где
,
где
![]() .
Данное свойство модуля вместе с первыми
двумя свойствами вводят на множестве
комплексных чисел структуру двумерного
нормированного пространства над полем
.
Данное свойство модуля вместе с первыми
двумя свойствами вводят на множестве
комплексных чисел структуру двумерного
нормированного пространства над полем
![]() .
.
-
Для пары комплексных чисел z1 и z2 модуль их разности | z1 − z2 | равен расстоянию между соответствующими точками комплексной плоскости.
Аргументом комплексного числа z
= a + ib (z ≠ 0) называется величина угла
φ между положительным
направлением действительной оси и
вектором
![]() и
обозначается
и
обозначается
![]() .
.
Величина угла φ считается положительной, если угол φ отсчитывается против часовой стрелки, и отрицательным в противном случае.
-
Для комплексного нуля значение аргумента не определено, для ненулевого числа z аргумент определяется с точностью до 2kπ, где k — любое целое число.
-
Главным значением аргумента называется такое значение
 ,
что
,
что
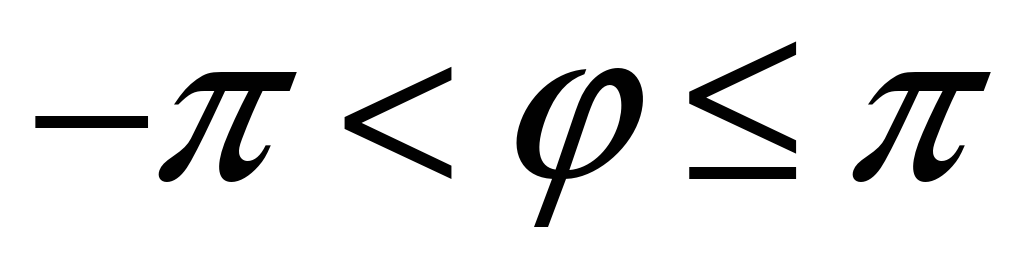 .
Часто главное значение обозначается
.
Часто главное значение обозначается
 .
Главное значение аргумента обратного
числа отличается знаком от аргумента
исходного:
.
Главное значение аргумента обратного
числа отличается знаком от аргумента
исходного:
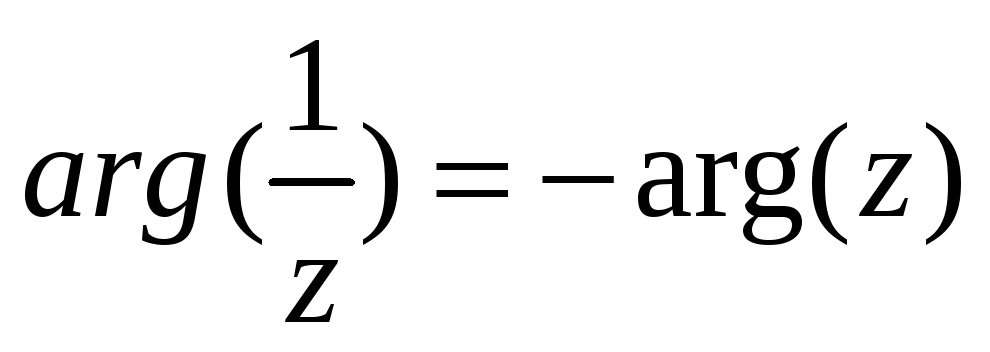 .
. -
 -множество
аргументов числа z
-множество
аргументов числа z
Операции над комплексными числами.
Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что i2 = − 1):
(a + ib) ± (c + id) = (a ± c) + i(b ± d)
![]() ;
;
![]()
При делении комплексных чисел
![]() нужно числитель и знаменатель умножить
на число, сопряженное к знаменателю.
Тогда в знаменателе окажется действительное
число
нужно числитель и знаменатель умножить
на число, сопряженное к знаменателю.
Тогда в знаменателе окажется действительное
число
![]() — на которое можно поделить:
— на которое можно поделить:
![]()
![]()
Возведение в степень:
![]()
Извлечение корня:
По формуле Муавра: zn = [r(cos φ + isin φ)]n = rn(cos nφ + isin nφ), где де r — модуль, а φ — аргумент комплексного числа получаем:
![]()
