А. Р. Лакерник. Высшая математика.Краткий курс

I. Теория пределов. Непрерывность функций

зу) на некотором множестве, если множество ее значений на это м множестве является ограниченным сверху (снизу).

Функция y = f (x) называется ограниченной при x ® a сверху (снизу), если она ограничена сверху (снизу) в некоторой про колотой окрестности точки а.

Ограниченные сверху и снизу последовательности и функции называются просто ограниченными.

Таким образом, {хn} ограничена Ы $M > 0 : "nОN (| xn |£ M ).

Замечание. Покажем, что для этого достаточно, чтобы последнее неравенство выполнялось n > m, где m – некоторое число. Если для n > m выполняется | xn |≤ M, то взяв в качестве М1 максимальное из чисел |x1|,

	|x2|,..., |xm|, М, найдем, что n N (| xn	|≤ M1).	0
	Функция f (x) ограничена при	x → a M > 0 è
			δ > 0 : x U (a,δ)
	( | f (x) |≤ M ).

	Теорема 2.2. Если последовательность (функция) имеет конечный
предел, то она ограничена (при x ® a ).
	¡ 1. Пусть существует lim x = a. Возьмем произвольное e > 0 Ю
Þ	x→∞ n
	$N > 0: "n > N ( | xn - a |< e ). Íî | xn - a |³| xn | - | a | Þ "n > N
( |	xn | - | a |< e , | xn |<| a | +e ). Взяв M =| a | +e, получаем ограниченность

последовательности {xn}.

2. Пусть существует lim f (x) = a. Возьмем произвольное e > 0 Ю

x→a

Þδ > 0: x, 0 <| x − a |< δ ( | f (x) − b|< ε ). Íî | f (x) – b| ³ |f (x)| – |b| Þ

Þ" x, 0 <| x − a |< δ (|f (x)| – |b| < e , |f (x)| <| b | +e ), ÷òî (ïðè M =| b | +ε ) и означает ограниченность функции y = f (x) при x ® a . x

Задачи. Доказать, что:

1) åñëè õn £ b è $			lim x	= a,	òî a £ b (èëè åñëè õn ³	b è
			x→∞ n
lim x	= a,	то a ³ b). То есть надо доказать, что если вся последователь-
$ x→∞ n

ность не превосходит b и имеет предел a, то этот предел тоже не превосходит b;

2. Предел последовательности и предел функции

0

2) если в некоторой U (a) f (x) £ c и $ lim f (x) = b, то b £ c (или если

x→a

		0	è $ lim	f (x) = b, òî b ³ c);
в некоторой U (a) f (x) ³ c
			x→a
3)	lim c = c è lim c = c.
	→∞	x→a
	n

¡1) õn £ b, lim xn = a. Будем доказывать методом «от противного».

n→∞

Пусть a > b. Рассмотрим окрестность U(a), такую, что "x ОU (a) (х ³ b). Согласно определению 2.3 $ N : "n > N (xnÎ U (a)) Þ õn ³ b, ÷òî ïðî-

тиворечит условию (рис. 6). Аналогично рассматриваются ост альные случаи примеров 1 и 2;

b	a	x

Ðèñ. 6

3) здесь очевидно, что N > 0 и d > 0 можно взять любыми числами. x

2.2.Бесконечно малые последовательности и функции

èих свойства

Определение 2.8. Последовательность {xn} называется бесконечно

малой (б.м.), если lim x n = 0 . Функция y = f (x) называется бесконеч- n→∞

но малой при x ® a (б.м., x ® a ), если lim f (x) = 0.То есть

x→a

{xn} – á.ì. Û "e > 0 $N = N (e): "n > N (| xn |< e);

0

y = f (x) – á.ì., x ® a Û "e > 0 $d = d(e): "x ÎU (a,d) (| f (x)|< e).

Теорема 2.3. Сумма двух бесконечно малых последовательностей (функций при x ® a ) есть последовательность (функция при x ® a ) бесконечно малая.

¡ 1. Пусть {xn}, {yn} – б.м. Докажем, что {xn + yn} – á.ì., ò.å.

"e > 0 $N = N(e): "n > N (| xn + yn |< e).

26

27

I. Теория пределов. Непрерывность функций

Возьмем произвольное e > 0 , тогда

$N1 : "n > N1 (| xn |< e / 2) è $N2 :"n > N2 (|yn |< e /2),

Þ "n > N = max(N1,N2) (| xn + yn |£| xn | + | yn |< e / 2 + e / 2 = e).

2. Пусть	y = f (x), y = g(x) – б.м., x ® a . Докажем, что
y = f (x) + g(x)	– á.ì., x ® a , ò.å.

		0
	"e > 0 $d = d(e): "xÎU (a,d) (| f (x)+ g(x)|< e).
Возьмем произвольное e > 0 , тогда
	0	0
$d1 : "x ÎU (a,d1) (| f (x) |< e / 2)		è $d2 :"x ÎU (a,d2)(|g(x)|< e /2),
0		(x) |£| f (x) | + | g(x) |< e / 2 + e / 2 = e). x
Þ "x ÎU	(a,min(d1,d2 )) (| f (x) + g

Теорема 2.4. Произведение бесконечно малой последовательности (функции при x ® a ) на ограниченную последовательность (функцию при x ® a ) есть последовательность (функция при x ® a ) бесконечно малая.

¡ 1. Пусть {xn} – á.ì., {yn} – ограниченная, |yn| £ M. Докажем, что {xnyn} – á.ì., ò.å.

"e > 0 $N = N(e): "n > N (| xnyn |< e).

Возьмем произвольное e > 0 , тогда

$N : "n > N(| xn |< e /M ) Þ "n > N (| xnyn |=| xn || yn |< Me M = e). 2. Пусть f (x) – б.м., x ® a , g (x) – ограниченная при x ® a , т.е.

0

$d1 : "x ÎU (a,d1) (| g(x) |< M ).

Докажем, что f (x)g (x) – б.м., x ® a , т.е. "e > 0 $d = d(e) > 0 , такое, что

0

"xÎU (a,d) (| f (x)g(x)|< e).

2. Предел последовательности и предел функции

Возьмем произвольное e > 0 Ю $d2 , такое, что

0			0
"x ÎU	(a,d2 ) (| f (x) |< e / M )Þ "x ÎU			(a,min(d1,d2))
	(| f (x)g(x)|=| f (x) || g(x)|<	e	M = e).		x
		M

Ниже приведены три следствия из теорем 2.3 и 2.4.

Следствие 1. Произведение двух б.м. последовательностей (или функций) есть последовательность (или функция) б.м. (так ка к бесконечно малая имеет конечным пределом 0, а любая последовате льность или функция, имеющая конечный предел, ограничена, то можно применить теорему 2.4).

Следствие 2. Произведение б.м. последовательности (или функции) на постоянное число есть последовательность (или фун кция) б.м. (так как постоянное число можно рассматривать как ограни ченную последовательность или функцию).

Следствие 3. Разность двух б.м. последовательностей (или функций) есть последовательность (или функция) б.м. (для последовательн о-

ñòåé: xn - yn = xn + (-1)yn, здесь xn – б.м. по условию, а (–1) yn – б.м. по следствию 2; значит, xn + (-1)yn – б.м. по теореме 2.3; аналогично для функций: f (x) - g(x) = f (x) + (-1)g(x) и т.д.).

Теорема 2.5. Частное от деления бесконечно малой последовательности (функции при x ® a ) на последовательность (функцию), имеющую (при x ® a ) конечный и отличный от 0 предел, есть последовательность (функция при x ® a ) бесконечно малая.

¡		xn	= x		1		, {x		} – á.ì. è $ lim y		= b ¹ 0;
		yn		n yn			n		n→∞	n
	f (x)			= f (x)			1	, f (x) – á.ì. è $ lim g(x) = b ¹ 0 Þ
	g(x)						g(x)
									x→a

в силу теоремы 2.4 для доказательства теоремы достаточно показать ог-

	ì	1	ü	1
	раниченность íï		ýï или ограниченность при x ® a функции		.
				g(x)
	ï y		ï
	î	n þ

28

29

I.Теория пределов. Непрерывность функций

1.В определении предела 2.1 возьмем e = | b2 | Þ

$N : "n > N æ

| y

n

- b

|<

|

b | ö

. Íî

| y

- b |=| b - y |³| b | -

| y

n

|Þ

ç

÷

n

n

è

2 ø

æ

| yn |<

|

b | ö

"n > N ç| b | -

2

÷ .

è

ø

Теперь, перенеся |y | в правую, а | b |

– в левую часть неравенства, полу-

n

2

| b |

1

2

ì

1

ü

÷èì

ï

ï

– ограничена.

| yn |>

Û

<

Þ í

ý

2

| y

n

|

| b |

ï y

ï

î

n

þ

| b | Þ

2. Теперь в определении предела 2.5 возьмем e =

æ

|b | ö

2

0

$d >

0: "xÎU (a,d)ç

| g(x) - b |<

÷.

Íî | g(x) - b |=| b - g(x) |³| b | - | g(x)|

2

æ

è

| b |

ø

| b |

1

2 ö

0

Þ "xÎU (a,d) ç| b | - | g(x)|<

Û| g(x)|>

Û

<

÷ Þ

2

2

| g(x)|

è

| b | ø

1

ограничена. x

g(x)

2.3. Связь существования предела с бесконечно малыми. Основные теоремы о пределах

Теорема 2.6. Для того чтобы предел последовательности (функции при x ® a ) был равен некоторому числу b, необходимо и достаточно, чтобы эту последовательность (функцию) можно было предст авить в виде суммы числа b и бесконечно малой последовательности (функции при x ® a ). То есть

lim xn = b Û xn = b + an,

n→∞

ãäå {an} – последовательность б.м.;

lim f (x) = b Û f (x) = b + a(x), x→a

где a(x) – функция б. м., x ® a .

2.Предел последовательности и предел функции

¡Необходимость.

1. Пусть lim xn = b Û "e > 0$N = N(e): "n > N (| xn - b |< e).

n→∞

Положим

xn − b = αn, xn = b + an Þ "e > 0$N = N(e):"n > N (| an |< e) Þ {an} – б.м. 2. Пусть

0

lim f (x) = b Û "e > 0$d = d(e) > 0 : "x ÎU (a,d) (| f (x) - b |< e). x→a

Положим

0

f (x) - b = a(x), f (x) = b + a(x) Þ "e > 0$d = d(e) > 0: "xÎU (a,d) (| a(x)|< e) Þ a(x) – á.ì., x ® a .

Достаточность.

1.Пусть xn = b + αn, {αn}–á.ì. Û "e > 0$N = N (e):"n > N (| an |< e). Íî an = xn - b Þ "e > 0$N = N(e): "n > N (| xn - b |< e), но это и означа-

åò, ÷òî lim xn = b (см. определение 2.1).

n→∞

2. Пусть		f (x) = b + a(x), a(x) – á.ì., x ® a Û "e > 0		$d = d(e):
0	(a,d) (| α(x)|< ε). Íî a(x) = f (x) - b Þ "e > 0			0
"x ÎU			$ d = d(e): "xÎU(a,d)

(| f (x) − b |< ε), ноэтоиозначает,что lim f (x) = b (см.определение2.5).x

x→a

Теорема 2.7. Предел суммы двух последовательностей (функций) равен сумме пределов этих последовательностей (функций) , если эти пределы существуют.

¡ 1. Пусть lim xn = a, lim yn = b Ю (по теореме 2.6 (необходимость)

n→∞ n→∞

xn = a + an, yn = b + bn, ãäå { an } è { βn } – б.м. Сложим оба этих равенства: xn + yn = (a + b) + (αn + βn). В этой формуле a+ b – число, αn +bn –

б.м. по теореме 2.3		Ю по теореме	2.6 (достаточность)
lim(xn + yn) = a + b.
n→∞	x→af (x) = b,	x→ag (x) = c Ю по теореме 2.6 (необходимость)
2. Пусть
	lim	lim
f (x) = b + a(x), g(x) = c + b(x), ãäå a(x) è b(x)			– б.м., x ® a . Сложим

30

31

I. Теория пределов. Непрерывность функций

оба этих равенства: f (x) + g(x) = (b + c) + (a(x) + b(x)). В этой формуле (b + c) – число, a(x) +b(x) – б.м. по теореме 2.3 Ю по теореме 2.6 (до-

статочность) lim( f (x) + g(x)) = b + c. x

x→a

Теорема 2.8. Предел произведения двух последовательностей (функций) равен произведению пределов этих последовател ьностей (функций), если эти пределы существуют.

¡ 1. Пусть lim xn = a, lim yn = b Ю по теореме 2.6 (необходимость)

n→∞ n→∞

xn = a + an, yn = b + bn, ãäå { αn } è {bn } – б.м. Перемножим эти равенства: xnyn = ab + (aβn + bαn + αnβn). В этой формуле ab – число, а выражение aβn + bαn + αnβn – б.м. по следствиям теоремы 2.4 и теореме 2.3

Ю по теореме 2.6 (достаточность) lim x y = ab.
2. Пусть	x→af (x) = b,	n→∞ n n
		x→ag (x) = c Ю по теореме 2.6 (необходи-
	lim	lim

мость) f (x) = b + a(x), g(x) = c + b(x), где a(x) и b(x) – б.м., x ® a Ю f (x)g(x) = bc + (bb(x) + ca(x) + a(x)b(x)). В этой формуле bc – число, а выражение bb(x) + ca(x) + a(x)b(x) – б.м. по следствиям теоремы 2.4

и теореме 2.3 Ю по теореме 2.6 (достаточность) lim f (x)g(x) = bc. x
				x→a
Следствие 1. Постоянный множитель можно выносить за знак
предела.
¡ По теореме 2.8 lim cx		= lim c lim x	= c lim x	(òàê êàê lim c = c –
n→∞	n	n→∞ n→∞ n	n→∞ n	n→∞

см. задачу 3 разд. 2.1), если последний предел существует. Так

же limcf (x) = limc Ч lim f (x) = c lim f (x), если последний предел суще-
x→a	x→a x→a	x→a

ствует. x

Следствие 2. Предел разности двух последовательностей (функций) равен разности пределов этих последовательностей (функц ий), если эти пределы существуют.

¡ Применяя теорему 2.7 и следствие 1, имеем:

1) lim(x - y			) = lim(x		+ (-1)y	) = lim x	+ lim(-1)y		= lim x +
n→∞ n		n	n→∞	n	n	n→∞ n	n→∞	n	n→∞ n
+(-1)lim y		= lim x		- lim y .
n→∞	n		n→∞ n	n→∞ n

32

2. Предел последовательности и предел функции

2) lim( f (x) - g(x)) = lim( f (x) + (-1)g(x)) = lim f (x) +
x→a	x→a	x→a

+ lim(-1)g(x) = lim f (x) + (-1)lim g(x) = lim f (x) - limg(x). x
x→a	x→a	x→a	x→a	x→a
Теорема 2.9. Предел отношения двух последовательностей (фун-

кций) равен отношению пределов этих последовательностей (функций), если эти пределы существуют и предел знаменателя отличен от 0.

¡ 1. Пусть lim xn = a, lim yn = b Ю по теореме 2.6 (необходимость)

n→∞

n→∞

xn = a + αn, yn = b + βn, ãäå a(x) è b(x) – á.ì. Þ

xn

=

a + an

= a

+ çæ

a + an

- a

÷ö

= a

+

ab + ban - ab - abn

= a +

ban - abn

.

y

b + b

n

b

ç b + b

n

b ÷

b

b(b + b

n

)

b b(b + b

n

)

n

è

ø

По теореме 2.5 последняя дробь есть б.м., так как ее числитель – б.м. по следствиям 2 и 3 из теорем 2.3 и 2.4 и

$lim b(b + b		) = b lim(b + b	n	) = b(b + 0)	= b2	¹ 0
n→∞	n	n→∞

(здесь были применены: следствие 1 теоремы 2.8, теорема 2.7 и сво й-

ства пределов lim b = b, lim b = 0 ); теперь по теореме 2.6 (достаточ-

n→∞

n→∞

n

ность, a – число)

lim

xn

= a .

b

n→∞ yn

b

2. Пусть lim f (x) = b,

lim g (x) = c Ю по теореме 2.6. (необходимость)

x→a

x→a

(x)

è b(x)

– á.ì.,

x ® a

Þ

f (x) = b + a(x), g(x) = c + b(x), ãäå a

f (x)

b + a(x)

b

æ b + a(x)

b ö

b

ca(x) - bb(x)

=

=

+

ç

-

÷ =

+

.

g(x)

c + b(x)

c

c

c(c + b(x))

è c + b(x)

c ø

По теореме 2.5 последняя дробь есть б.м., так как ее числитель – б.м. и

$lim c(c + b(x)) = clim(c + b(x)) = c2 ¹ 0 Þ
x→a	x→a

	по теореме 2.6 (достаточность,	b	– число)	lim	f (x)		= b .	x
		c			g(x)
	Замечания.			x→a			c

1.Теоремы о пределах функций справедливы и при a = ¥.

2.В теоремах о пределах последовательностей и функций доп ускаются и бесконечные пределы, если это имеет смысл:

33

I. Теория пределов. Непрерывность функций

(+¥)+ (+¥) = +¥; (-¥)+ (-¥) = -¥; (+¥)- (-¥) = +¥; ¥ × ¥ = ¥;

b× ¥ = ¥ (b ¹ 0);	b	= 0 (b ¹ ¥);	b	= ¥ (b ¹ 0).
	¥		0

0¥

3.(+¥) +(–¥); 0× ¥; 0; ¥ и т.д. – это так называемые неопределенности (т.е. случаи, где основные теоремы о пределах сразу не приме нимы).

Примеры раскрытия неопределенностей. Найти пределы. Р е ш е н и е

3

5

2n2 - 3n + 5

2 - n

+

=

2 (неопределенность вида ¥ ; ÷èñ-

1)

lim

= lim

n2

n→∞ 3n2 + 4n - 7

n→∞

4

7

3

¥

3 +

-

n

2

n

литель и знаменатель почленно поделены на n2);

2)

lim

x2

+ 5x - 6

= lim

(x + 6)(x -1)

= lim

x + 6

=

7

= -1

(неопределен-

- 9x + 8

(x - 8)(x -1)

-7

x→1 x2

x→1

x→1 x - 8

ность вида

0 ; в числителе и знаменателе выделен приводящий к ней мно-

0

житель х – 1).

2.4.Некоторые теоремы

îпределах последовательностей и функций

Определение 2.9. Последовательность {xn} называется неубывающей (невозрастающей), если для всех nОN выполняется следующее условие: xn+1 ³ xn (xn+1 £ xn); последовательность называется монотонной, если она является либо неубывающей, либо невозрастающей.

Теорема 2.10. Любая ограниченная сверху неубывающая последовательность имеет конечный предел. Любая ограниченная сн изу невозрастающая последовательность имеет конечный предел. Или , объединяя эти утверждения: любая ограниченная монотонная после довательность имеет конечный предел.

¡ Докажем, что любая ограниченная сверху неубывающая последовательность имеет конечный предел. Нам дано, что {xn} – неубывающая ( xn+1 ³ xn ) и ограниченная сверху последовательность ( xn £ M, где М – некоторое число). Надо доказать, что существует конечный предел

этой последовательности lim xn . По теореме 1.1 существует верхняя

n→∞

2. Предел последовательности и предел функции

грань ограниченного сверху множества значений этой посл едовательности sup {xn} = a (ðèñ. 7).

a M	x
Ðèñ. 7

Докажем, что lim xn = a. Зададим произвольную окрестность точ-

n→∞

ки а U (a,e) и докажем, что, начиная с некоторого номера, все члены последовательности {xn} попадут в эту окрестность (рис. 8).

a –e

a

a + e

x

Ðèñ. 8

По определению верхней грани имеем xn £ a и существует n0 , òà-

êîå, ÷òî xn 0 > a – e. Тогда при n > n0 имеем xn > xn 0 > a – e, à ýòî è îçíà- ÷àåò, ÷òî xn ÎU(a,e). x

Определение 2.10. Последовательность называется сходящейся, если она имеет конечный предел.

Определение 2.11. Подпоследовательностью последовательности {xn} называется любое бесконечное подмножество членов этой п оследовательности {xnk }, k = 1,2,3,...

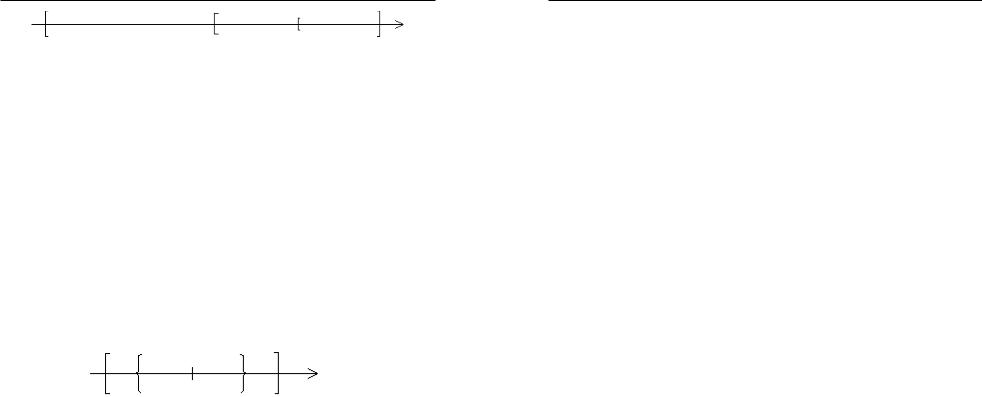
Теорема 2.11 (Больцано—Вейерштрасса).

У любой ограниченной последовательности существует схо дящаяся подпоследовательность.

¡ Пусть последовательность {xn} ограничена. Тогда существует отрезок [ a, b ], такой, что для любого номера nО N все xn принадлежат этому отрезку (рис. 9). Разделим этот отрезок пополам. Пу сть [ a1, b1 ] – та половина, которая содержит бесконечное число членов исходной последовательности (если обе половины такие, то бе рем любую

из них). Выберем произвольный x О йa , b щ. Разделим отрезок n1 ë 1 1û

[ a1, b1 ] пополам. Пусть [ a2, b2 ] – та половина, которая содержит бесконечное число членов исходной последовательности (если обе половины такие, то берем любую из них). Выберем произвольный

x	Î éa	2	, b	ù	сномером n	> n . Разделимотрезок[ a	2	, b	2	]пополамит.д.
n2	ë			2 û	2	1

34

35

I. Теория пределов. Непрерывность функций

α		β	x
α1		β1
α	2	β2

Ðèñ. 9

Полученная система вложенных отрезков с длинами, стремящ имися к нулю, согласно теореме 1.2 и замечания к ней имеет единст венную

общую точку a [αn, βn] для всех n. Теперь докажем, что lim xn = a.
k→∞	k

Возьмем произвольную e -окрестность точки а (на рис. 10 обозначена квадратными скобками). Тогда существует отрезок [ ak0 , bk0 ], целиком лежащий в нашей окрестности (на рис. 10 обозначен фигурными скобками). Тогда все следующие отрезки тоже будут лежать в этой окрест-

ности. Значит, все точки xn						, у которых k > k0, лежат в этой окрестно-
					k
ñòè. Èëè: $k0 : "k > k0 ([ak ,bk ]ÎU (a,e)) Þ "k > k0									( xn ÎU (a,e)).x
									k
									x
				a − ε	αk	a	βk	a + ε
					0		0
							Ðèñ. 10
	Теорема 2.12 (о промежуточной последовательности / функции).
	1. Пусть {xn}, {tn}, {yn} – три последовательности и									"nÎN
( x	≤ t		≤ y	). Пусть существуют конечные пределы lim x						= a è
n		n	n						n→∞ n
lim yn = a Ю существует и предел lim tn = a.
n→∞							n→∞
	2. Пусть функции y = f (x), y = j(x), y = g(x)								определены в неко-
			0	0	(a) ( f (x) £ j(x) £ g(x)). Пусть существуют конеч-
торой U (a)				è "x ÎU
ные пределы lim f (x) = b						и lim g(x) = b Ю существует и предел
				x→a		x→a

limj(x) = b.

x→a

2. Предел последовательности и предел функции

¡ 1. Возьмем произвольное e > 0 Ю $ N1: n > N1 ( xn U(a,ε) );

$ N	: n> N	2	( y U(a,ε) ) Þ "n > N = max(N		,N	) ( x U(a,ε) è
2			n	1	2		n
yn ÎU (a,e) ) Þ "nÎN (tn ÎU (a,e) ).						0
2. Возьмем произвольное e > 0 Ю				$ δ1 > 0: "x ÎU			(a,d1)
			0				0
( f (x)ÎU(b,e)); $ d2 > 0: "x ÎU (a,d2) (g(x)ÎU(b,e)) Þ							"xÎU (a,d),
							0
ãäå	d = min(d1,d2) ( f (x)ÎU (b,e) è g(x)ÎU (b,e)) Þ "x ÎU (a,d)

(j(x)ÎU (b,e)). x

Теорему 2.12 иногда называют теоремой «о двух милиционерах» .

Замечание. В случае функций теорема верна и при a = +∞.

¡ Возьмем произвольное e > 0 Ю $ N1 > 0: "x > N1 ( f (x)ÎU (b,e) ); $ N2 > 0: x > N2 (g(x)ÎU (b,e)) Þ "x > N,ãäå N = max(N1,N2)

( f (x)ÎU (b,e) è g(x)ÎU (b,e)) Þ "x > N (j(x)ÎU (b,e)). x

Теорема 2.13 (о пределе сложной функции). Пусть дана сложная

функция y = j(x), z = f (y), т.е. z = f (j(x)). Пусть			x→aj(x) = c è
			lim
	0		lim f (j(x)) =
lim f (y) = b è "xÎU (a) (y ¹ c) Þ lim f (j(x)) = b (èëè
y→c		x→a	x→a
= lim f (y) – формула замены переменной).
y→c		0
¡ Докажем, что "e > 0
		$ d = d(e) > 0: "xÎU (a,d) (z ÎU (b,e)). Âîçü-
	e > 0	0
мем произвольное		Ю $ s > 0: "y ОU (c, s) (z ОU (b, e)). Далее
0	0
$ d > 0: "xОU (a,d) (y ОU (c,s)) (при достаточно малом d y ¹ c по усло-
0	0
âèþ) Þ "xÎU (a,d) (y ÎU (c,s) Þ z ÎU (b,e)). x

Определение 2.12. Говорят, что последовательность {xn} удовлетворяет критерию Коши, или, что то же самое, является фундаменталь-

íîé, åñëè "e > 0 $N = N(e): "n,m > N (|xn – xm | < e).

Теорема 2.14. Для того чтобы последовательность {xn} сходилась, необходимо и достаточно, чтобы она удовлетворяла кр итерию Коши.

36

37

I.Теория пределов. Непрерывность функций

¡Пусть lim→∞ xn = a. Возьмем произвольное e > 0 Ю $ N: "n > Nn

( |xn – a | < e / 2) Þ " n,m > N ( |xn – xm | = |(xn – a) + (a – xn) | £ |xn – a | + + |xm – a | < e / 2 + e / 2 = e) Þ {xn} удовлетворяет критерию Коши.

Пусть, наоборот, {xn} удовлетворяет критерию Коши, т.е. "e > 0 $N = N (e):"n,m > N (| xn - xm |< e). Òàê êàê | xn – xm | ³ |xn | – | xm |, òî |xn | – |xm | < e, |xn | < |xm | + e. Если в этом неравенстве m зафиксировать, то,

по замечанию к определению 2.7, {xn} ограничена. Тогда по теореме 2.11 из этой последовательности можно выделить сходящуюся по дпоследо-

вательность: lim xn = a, где а – некоторое число. Докажем, что тогда и
		k→∞	k
lim x = a.			Возьмем	произвольное	e > 0	Þ
n→∞	n
$k0	:"k > k0	(|xn	-a |< e /2).Поусловию $ N: "n,m > N (| xn - xm |< e / 2).
		k

Пусть n > N и k > k0		таково, что nk > N (такое k существует, так как
lim n	= ¥) Þ "n > N	(| xn	- a |= |(xn	- xn	) + (xn - a)|£| xn	- xn | +
k→∞ k				k	k	k
+ | xn	- a |< e /2 + e /2 = e) Þ lim xn = a Þ {xn} сходится. x
k			→∞
			n

2.5. Некоторые замечательные пределы

Теорема 2.15 (первый замечательный предел).

				lim sin x		=	1.	(2.1)
				x→0	x
æ	0,	p ö		. Как видно из рис. 11, площадь треуголь-
¡ Пусть сначала x Оç		2	÷
è			ø

ника ОМА меньше площади сектора ОМА, а последняя меньше площади треугольника ОСA. Площадь сектора с углом х находится по формуле

S круга

pr2

1

2

1

1

2

1

S =

2p

x = 2p x =

2r

x, значит, 2

|OA | | MB |< 2

|OA

|

x < 2 |OA | |CA |.

Здесь |ОА| = 1, |МВ| = sin x, |СА| = tg x Ю

1 sin x <

1 x <

1 tg x,

èëè

2

2

2

sin x < x < tg x.

2. Предел последовательности и предел функции

	Разделим все части последнего				y
неравенства на sin x > 0 (угол x на-					1	C
ходится в первой четверти):						M
1<	x	<	1	Þ cos x < sin x < 1.
	sin x		cos x
				x

Все функции в последней фор-
муле четные, следовательно, она
	æ	-	p	ö		x				1
справедлива и для x Оç			2	,0÷.
	è			ø			B			A x
Теперь перейдем к пределу при						Ðèñ. 11
	применяя теорему 2.12:
x ® 0,
lim1 = 1, значит, lim sin x				будет равен 1, если сумеем доказать, что
x→0	x→0	x
limcos x = 1 или согласно определению предела функции
x→0
					æ		2 x			ö
	"e > 0$d = d(e): "x, | x				|< dç| cos x - 1|< e Û 2sin				< e ÷.
							2
					è					ø

В этом определении x достаточно мало. Далее имеем в виду, что для

æ

p

p

ö

x

x

x Îç -

,

÷ sin2

< 1. Òàê êàê

ïðè

y < 1

y2 <| y |,

òî

2sin2

<

2

2

2

2

è

ø

x

|

x |

< 2

sin

=

2

sin

. Учитывая, что в первой четверти sin x < x, имеем:

2

2

2

sin |

x |

<

2 | x |

=

| x |. Теперь

вместо

выполнения

неравенства

2

2

2sin2

x

< e

íàì

достаточно потребовать,

чтобы | x | <

e (тогда

2

2sin2

x

< | x | < e), значит, в качестве d годится любое число: d £ e (тогда

2

| x |< δ ≤ ε Þ | x | < e). x

Примеры. Найти пределы функций.

Ð å ø å í è å

1) lim tgx = lim

sinx

= lim sin x lim

1

= 1×1

= 1;

(2.2)

x→0

x

x→0 xcosx

x→0 x

x→0 cosx

38

39

I. Теория пределов. Непрерывность функций

2)

lim

1- cos x

= lim

(1- cos x)(1+ cos x)

= lim

1- cos2 x

=

x2

x2(1+ cos x)

x2

(1+ cos x)

x→0

x→0

x→0

= lim

æ sin x ö2

1

=

1

.

(2.3)

ç

÷

x

1+ cos x

2

x→0

è

ø

Выражения (2.2) и (2.3) можно использовать для вычисления други х пределов.

Теорема 2.16 (второй замечательный предел для последовательностей).

æ	+	1 ön					(2.4)
lim ç1		÷ = e.
n→∞ è		n ø
			ì			1 ö	n ü
¡ Рассмотрим последовательность {an			ïæ		+		ï
			} = íç1			÷	ý.
			ï	è		n ø	ï
			î				þ

Согласно теореме 1.5 представим аn в виде суммы (n + 1) слагаемых:

n

1

n

1

an = åCnk

= 1+ å

n(n - 1)...(n -k + 1)

=

k

k

k=0

n

k=1

k!

n

n

1

æ

1 öæ

2ö æ

k - 1ö

= 1+ å

ç

1

-

֍

1-

÷ ...ç1-

n

÷

k=1 k !è

n øè

n ø è

ø

(в последнем преобразовании мы каждую скобку поделили на n). При переходе от an ê an+1, т.е. при замене n на n + 1, знаменатели

дробей возрастают, значит, каждая разность 1- ni становится больше, т.е. в нашей сумме увеличивается каждое слагаемое и, кроме т ого, добавляется еще одно (n + 2)-е неотрицательное слагаемое, значит, для

"nÎN an+1 > an Þ {an} возрастает (отсюда, кстати, an > a1 = 2).

Далее проверим, что эта последовательность ограничена св ерху; для этого заменим в последней сумме каждую скобку на 1 (от чего каждая скобка и вся сумма могут только вырасти). Так как первые дв а слагаемых в нашей сумме (при k = 0 и k = 1) равны 1, то

n	1		n		1	n	1	n	1
an < 1+ å			= 2 + å			< 2+ å		= 2+å		.
					2× 3× 4×...× k		2× 2× 2× ...× 2		k−1
k=1 k!			k=	2		k=2		k=2	2

Последняя сумма является суммой геометрической прогрес сии сn – 1 членами, у которой q = 12, à b1 = 12 , значит,

2. Предел последовательности и предел функции

an < 2 + b1(1- qn−1) = 2 + 1/2(1- (1/2)n−1 ) = 2 + (1- (1/2)n−1)< 2+ 1= 3 Þ 1- q 1- 1/2

{an } ограничена сверху.

Последовательность {an } возрастает и ограничена сверху, следова-

æ	1	+	1 ön
тельно, по теореме 2.10 она имеет конечный предел lim ç			÷	. Îáî-
n→∞ è			n ø

значая этот предел буквой е, получим нужное нам равенство. x

Òàê êàê 2 £ an £ 3, то 2 £ e £ 3 (см. разд. 2.1, задача 1). Можно показать, что е – иррациональное число и e » 2,71828.

Теорема 2.17 (второй замечательный предел для функций).

lim

æ

1

öx

= e.

(2.5)

ç1+

x

÷

x→∞

è

ø

¡ Пусть сначала x ® +¥. Для "x > 1 возьмем такое n = n(x)ОN,

÷òî

n £ x < n + 1 (это так называемая целая часть числа х), тогда

1

<

1

£

1

Þ

n +

1

x

n

1

1

1

æ

1 ön

æ

1öx

æ

1ön+1

1+

< 1+

£ 1+

Þ ç

1+

÷

<

ç 1+

÷

<

ç 1+

÷ .

n +1

x

n

n +

1

è

ø

è

x ø

è

n ø

Теперь пусть x ® +¥ Ю n ® ¥. Согласно теореме 2.16,

lim

æ

+

1

ön+1

æ

1+

1 ön

æ

+

1ö

ç1

n

÷

= lim ç

÷

limç1

n

÷ = e × 1= e;

n→∞

è

ø

n→∞ è

n ø

n→∞ è

ø

æ

1

ön

æ

1

ön+1

æ

1

ö

lim

ç1+

÷

= lim

ç1+

÷

: limç1

+

÷

= e :1= e.

n +

1

n +

1

n

n→∞

è

ø

n→∞

è

ø

n→∞ è

+ 1ø

Тогда по замечанию к теореме 2.12 существует

æ

+

1

öx

lim ç1

x

÷ = e.

x→+∞ è

ø

Пусть теперь x ® -¥. В соответствии с теоремой 2.13 произведем

замену y = -x :

æ

1 öx

æ

1

ö− y

æ

y öy

æ y -1+ 1öy

lim

ç1

+

x

÷

=

lim ç1

-

y

÷

=

lim

ç

÷

= lim

ç

÷ =

x→−∞ è

ø

y→+∞ è

ø

y→+∞

è y -1

ø

y

→+∞ è

y -1 ø

40

41

= b, b ¹ 0, b ¹ ¥. Если b = 1, то б.м. называются эквивалент-

I. Теория пределов. Непрерывность функций

æ

1 ö

y−1

æ

1 ö

6

æ

1

ö

x

ò.2.16

=

lim ç1

+

÷

ç

1+

÷

=

e ×1= e Þ limç

1+

÷

= e. x

y -1

y - 1

x

y→+∞ è

ø

è

ø

x→∞ è

ø

Примеры. Найти пределы функций.

Ð å ø å í è å

1. Покажем, что

1

После замены

В частности,

lim(1+ a(x))α(x)

x→a

a(x) = 1y , имеем

1

lim(1+ a(x))α(x)

x→a

1

lim(1+ x)x = e.

x→0

= e, a(x) – á.ì., x ® a.

(2.6)

æ	+	1	öy
= lim ç1		y	÷	= e.
y→∞ è			ø

(2.7)

2. Покажем, что

lim ln(1+ x)		= 1.	(2.8)
x→0	x

Используя непрерывность функции y = ln x (ниже будет показано, что именно для непрерывных функций символы предела и функции можно менять местами), имеем

ln (1+x )

1

1

1

2.7

lim

= lim

ln (1+x ) = lim ln (1+x ) x =ln lim (1+x ) x = ln e=1.

x→0 x

x→0 x

x→0

x→0

3. Покажем, что

lim

ex - 1

= 1.

(2.9)

x

x→0

Произведя замену y = ex - 1, x = ln(1+ y) и используя непрерывность функции y = ex , получим

	lim	ex - 1	= lim	y	= lim	1	2.8
							= 1.
		x		ln(1+ y)		ln(1+ y)
	x→0		y→0		y→0

y

Формулы (2.6)–(2.9) можно использовать для вычисления других пределов.

3.Непрерывность функции

2.6.Сравнение бесконечно малых

Определение 2.13. Пусть a = a(x) и b = b(x) – две б.м. функции, x ® a . Эти б.м. называются б.м. одного порядка при x ® a , если

$ lim a(x)

x→a b(x)

ными при x ® a (обозначение: a ~ b, x ® a ). Если b = 0, то a называется б.м. более высокого порядка, чем b при x ® a (обозначение: a = o(b), x ® a ).

Примеры эквивалентных бесконечно малых приведены выше. Д ля нахождения ряда пределов бесконечно малые удобно заменять эквивалентными им. А именно справедлива следующая теорема.

Теорема 2.18 (о пределе отношения бесконечно малых).

Пусть f(x) ~ a(x), x ® a , g(x) ~ b(x), x ® a и $ lim a(x)

= b Þ

x→a b(x)

$ lim

f (x)

= b, т.е. при вычислении пределов отношения бесконечно

g(x)

x→a

малые можно заменять эквивалентными им.

¡ lim

f (x)

= lim

f (x)

a(x)

b(x)

= lim

f (x)

lim

a(x)

lim b(x) = 1×b ×1 = b. x

x→a g(x)

x→a a(x) b(x) g(x)

x→a a(x) x→a b(x) x→a g(x)

Пример. Вычислить lim ln(1+ 3x2 ).

x→0 e2x2 -1

Ð å ø å í è å

Согласно предыдущим примерам ln(1+3x2) ~ 3x2 è e2x2 -1~ 2x2, поэтому

	lim	ln(1+ 3x2 )	= lim	3x2	=	3	.
		e2x2 -1		2x2		2
	x→0		x→0

3.НЕПРЕРЫВНОСТЬ ФУНКЦИИ

3.1.Непрерывность функции в точке

Определение 3.1. Пусть функция y = f (x) определена в некоторой окрестности точки x0. Эта функция называется непрерывной в точке х0, если предел функции в точке х0 равен значению функции в этой точке или если

42

43

x→x0

I. Теория пределов. Непрерывность функций

lim f (x) = f (x0).	(3.1)
x→x0

По определению предела функции, это равенство равносильн о тому, что

"e > 0 $d = d(e): "xÎU(x0,d) ( f (x)ÎU( f (x0),e))

ε > 0 δ = δ(ε): x, | x − x0 |< δ (| f (x) − f (x0) |< ε).

По сравнению с определением предела функции здесь опущен о условие x ¹ x0, òàê êàê ïðè x = x0 последнее неравенство заведомо верно.

Определение 3.1 равносильно условию lim[ f (x) - f (x0)] = 0. Îáî-

значим x - x0 = Dx – приращение аргумента, f (x) - f (x0) = Dy – приращение функции, соответствующее данному приращению арг умента,

тогда определение непрерывности 3.1 можно записать в виде lim Dy = 0.

x→0

Определение 3.2 (равносильное определению 3.1). Пусть функция y = f (x) определена в некоторой окрестности точки х0. Эта функция называется непрерывной в точке х0, если lim Dy = 0 или если бесконеч-

x→0

но малому приращению аргумента соответствует бесконечн о малое приращение функции.

Приведем основные свойства функций, непрерывных в точке.

Теорема 3.1 (ограниченность). Пусть y = f (x) непрерывна в точке

õ0, тогда она ограничена при x ® x0.

¡ Это есть частный случай теоремы 2.2 (функция, имеющая конеч- ный предел в точке, ограничена в окрестности этой точки). x

Теорема 3.2 (сохранение знака). Пусть y = f (x) непрерывна в точ-

êå õ0 è f (x0) > 0(< 0)Ю f (x)> 0(< 0) и в некоторой окрестности точки х0 (ðèñ.12).

y	y
	x0	x
x0	x

Ðèñ. 12

3. Непрерывность функции

¡Возьмемвопределениинепрерывностифункции e =

"xÎU (x ,d)	æ	| f (x) - f (x ) |<	| f (x0)|	Û
	ç
0		0	2
	è

	| f (x	0	)|			| f (x	) |ö
Û -					< f (x) - f (x0) <	0		÷.
	2					2
							ø

Перенесем f (x0) в левую и правую части неравенства:

| f (x0)| Þ $d : 2

f (x ) -

| f (x0)|

< f (x) < f (x

) +

| f (x0)|

.

0

2

0

2

Из последнего неравенства имеем следующее:

åñëè

f (x ) > 0,

òî "xÎU

(x

,d)

æ f (x) > f (x

) -

f (x0)

=

f (x0)

> 0

ö

;

÷

0

0

ç

0

2

2

è

ø

åñëè f (x ) < 0,

òî "xÎU

(x

,d)

æ f (x) < f (x

) -

f (x0)

=

f (x0)

< 0

ö

. x

÷

0

0

ç

0

2

2

è

ø

Теорема 3.3 (арифметические операции над непрерывными функциями). Пусть функции y = f (x) è y = g(x) непрерывны в точке х0. Тогда в этой точке непрерывны функции y = f (x) ± g(x), y = f (x)g(x) и (при

g(x0) ¹ 0 ) gf ((xx)).

¡ Поскольку все эти утверждения доказываются одинаково, то докажем только последнее из них. Согласно теореме 2.9 и оп ределению 3.1,

		f (x)			lim f (x)		f (x0)			f (x)
	lim			=	x→x0	=		Þ	функция		непрерывна
		g(x)			lim g(x)		g(x0)			g(x)
	x→x0
					x→x0

в точке x0. x

Теорема 3.4 (непрерывность сложной функции). Пусть z = f (j(x)) – cложная функция. Пусть функция y = j(x) непрерывна в точке х0, а функция z = f (y) непрерывна в точке y0 = j(x0). Тогда сложная функция z = f (j(x)) непрерывна в точке х0 (проще говоря, если сложная функция составлена из двух непрерывных, то она сама непре рывна).

44

45