æ -10		2 ö	и	æ 5		-2	ö	,
A = ç	1	÷		B = ç	-1	1	÷
è		-1ø		è			ø

и решим их:

vA			4		,	p	0		æ	1		,		6		ö	,	q	0		æ	3			,=		11	ö	,
	= -								ç					=		÷					ç							÷
			7							7												14					14
									è					7		ø					è							ø
vB		1	, p			0		æ 1				2		ö			q	0		æ 2				7		ö
	=							ç		, =				÷	,					ç		, =				÷ .
		3							3												9
								è				3		ø						è				9		ø

То есть, если каждый игрок будет применять свои стратегии в биматричной игре, исходя только из собственной матрицы выигрышей, то он найдет свой оптимальный выигрыш и оптимальную стратегию другого игрока.

Таким образом, в биматричной игре вновь встречаемся с антагонизмом. Только это не антагонизм интересов, а антагонизм поведения.

Кроме того, в биматричных играх, при наличии нескольких равновесных ситуаций, средние выигрыши игроков разнятся, и встает вопрос о том, какой ситуации следует отдать предпочтение.

И последнее. Достаточно сложной является и проблема перехода от качественных оценок ситуаций к количественным оценкам. То есть, если, например, в задаче «Преподаватель – Студент» принять другие количественные оценки выигрышей, то можно получить и другие ситуации равновесия.

3.4. Кооперативные игры

Выше мы рассматривали игры, в которых игроки не имели права вступать в соглашения, образовывать коалиции. Рассмотрим теперь так называемые кооперативные игры, в которых игроки могут вступать в соглашения, образовывать коалиции. Такие ситуации могут возникать особенно часто, если рассматриваются игры n лиц. Следует отметить, что при содержательном анализе процедур совместного принятия решений в таких коопе-

67

ративных играх необходимы дополнительные сведения, касающиеся возможных действий коалиций, их предпочтений, способов обмена ими информацией о принимаемых решениях и. дт. Рассмотрим, например, принципы принятия решений на примере биматричных игр.

Как отмечалось выше, равновесие является важнейшим принципом оптимальности в бескоалиционных играх, в которых не рассматривается образование коалиций. Коалиция является формой кооперации, направленной на увеличение персональных

возможностей	игроков, то	есть на увеличение	их	выигрышей.
В матричной игре кооперация игроков лишена			смысла, так		как
в такой игре	улучшение	положения одного	из	них	приводит

к ухудшению положения другого. Ситуация меняется при переходе от матричной игры к биматричной, так как в биматричных играх кооперация может улучшить положение обоих игроков. В биматричной игре имеется лишь одна нетривиальная коалиция (коалиция, состоящая более чем из одного игрока) — коалиция обоих игроков. Для пояснения отличий между индивидуальным

выбором решений обоими игроками и совместным принятием решения коалицией этих игроков рассмотрим следующий пример.

№ 3.4. Конкурс на реализацию проекта. Две фирмы участву-

ют в конкурсе на реализацию проекта, причем доход от реализации проекта составит 10 у.е. Каждая фирма может либо подать простую заявку на участие в конкурсе (затраты равны 1 у.е.), либо представить программу реализации проекта(затраты составят 3 у.е.). По условиям конкурса, если обе фирмы выбирают одинаковый способ подачи заявки, то заказ (и доход) на реализацию проекта делится между ними пополам. Если же фирмы выбирают различные способы действий, то предпочтение отдается фирме, которая представит программу. Требуется разрешить эту конфликтную ситуацию.

Решение. Представим описанную конфликтную ситуацию в виде биматричной игры. Игроками A и B здесь выступают фирмы, стратегия A1 (B1 ) — подача заявки на участие в конкурсе,

стратегия A2 (B2 ) — представление программы действий.

68

Количественно выигрыши игроков можно выразить следующим образом:

æ 4	-1ö	, B =	æ 4	7	ö
A = ç	÷		ç	2	÷ .
è7	2 ø		è -1		ø
Решив эту игру, найдем единственную равновесную ситуа-
цию p = q = 0 ,		или	{A2 , B2 } с H1 (0, 0) = H2 (0, 0) = 2 . В этом

случае каждая фирма получает прибыль, равную 2 у.е. Для этого обе фирмы должны представить программу действий и поделить пополам доход от реализации проекта.

Ни одному из этих игроков невыгодно отклоняться от этой стратегии, так как это может только уменьшить его выигрыш. Но если игроки одновременно отклоняются от оптимальной (равновесной по Нэшу) стратегии, то возникает ситуация {A1 , B1},

которая очевидно является более выгодной для обоих из них с выигрышем H1 (1, 1) = H2 (1, 1) = 4 . Однако переход к этой си-

туации возможен только как результат договора между игроками, что осуществимо лишь при создании коалиции этих игроков. Объединение игроков в коалицию требует как минимум возможности обмена информацией между ними. Если же игроки не могут обмениваться информацией, то каждый из них будет опасаться менять выбранную им чистую стратегию A2 (B2 ) на страте-

гию A1 (B1 ), так как это приводит к уменьшению выигрыша

отклонившегося игрока.

Рассмотренный пример демонстрирует важную особенность биматричных игр — возможность наличия противоречия между выгодностью и устойчивостью(положением равновесия). Дей-

ствительно, ситуация {A2 , B2 } является устойчивой, но невыгод-

ной; а ситуация {A1 , B1} — выгодной, но неустойчивой. Поэтому,

если игроки заключают между собой договор — обоим придерживаться стратегии {A1 , B1}, то этот договор будет находиться

69

под угрозой нарушения, так как каждому игроку выгодно его одностороннее нарушение.

При исследовании кооперативного аспекта в теории игр внимание обращается, как правило, не на ситуации игры, а на ее исходы. В соответствии с этим в основе оптимальности лежит идея выгодности.

Проанализируем, как может реализовываться идея выгодности в рамках неантагонистической игры двух лиц. Пусть Аi —

множество стратегий первого игрока, а Bj — множество страте-

гий второго игрока. Если игроки образуют коалицию, то они могут создавать любую ситуацию {Ai , Bj }, и, таким образом, реали-

зовать любой исход игры. Возникает вопрос, какой исход игры следует считать в этом случае наиболее выгодным для коалиции, то есть оптимальным для нее.

Так, в рамках №3.4 игроки, объединившись в коалицию, предпочтут исход {A1 , B1} исходу {A2 , B2 } , однако исходы

{A1 , B2 } и {A2 , B1} также являются «кандидатами» на оптимальность.

Вобщем случае для биматричной игры рассмотрение вопроса

оее оптимальности с точки зрения коалиции удобно представить

в геометрической форме. На координатной плоскости (Н1 , Н2 ) изобразим точки, координатами которых являются выигрыши

игроков	(	a ,b	)	для каждой	возможной ситуации A , B		j }	. При
		ij ij			{	i
этом возникает «картинка»,					похожая на ту, что	изображена
на рисунке 3.5.

Так как коалиция может выбирать любой из представленных девяти исходов, то фактически получается задача двухкритериальной оптимизации, где первый игрок стремится максимизировать критерий H1 , а второй — критерий H2 . Анализ такой мно-

гокритериальной задачи можно провести в два этапа. На первом этапе мы проводим мажорирование (доминирование) стратегий по Парето. Отбрасывая исходы, доминируемые по Парето, получаем множество Парето-оптимальных исходов. В примере,

70

представленном на рисунке 3.5, Парето-оптимальными являются исходы {4, 5, 6, 8}. Выбор оптимального исхода следует произ-

водить из множества Парето-оптимальных исходов. На втором этапе необходимо решить вопрос— какое из Парето-оптимальных решений следует считать оптимальным.

H2

8

6

9

4

2

1

5

3

7

0	H1

Рис. 3.5

На первом этапе игроки выступают как союзники, так как этот шаг выгоден обоим из них. Однако на втором этапе, при сравнении любых двух Парето-оптимальных решений, игроки из союзников превращаются в противников: так как увеличение выигрыша одного из них влечет за собой уменьшение выигрыша другого.

Для решения задачи нахождения оптимального исхода в кооперативной игре сделаем еще одно допущение: возможно использование не только чистых, но и смешанных стратегий.

71

Это приводит к тому, что вместе с двумя чистыми исходами (H1 , H2 ) и (H1¢, H2¢ ) коалиция может реализовать также исход:

l×(H1 , H2 ) + (1 - l)×(H1¢, H2¢ ) =

=(lH1 + (1- l)H1¢, lH2 + (1- l)H2¢ ),

где l Î[0, 1] . С геометрической точки зрения, это означает, что множество исходов биматричной игры превращается в многоугольник D, вершинами которого будут точки(aij ,bij ) . При

этом исходы, оптимальные по Парето, образуют «северовосточную» границу этого многоугольника, а именно, это ломаная

(8, 6, 4, 5) (рис. 3.6):

H 2	8	6
9
		4
1	2
3	7	5

0

H1

Рис. 3.6

Задача нахождения кооперативного решения биматричной игры сводится теперь к построению правила, которое для каждого такого многоугольника исходов указывает единственный оптимальный исход, принадлежащий его «северо-восточной»

72

границе. Рассмотрим решение этой задачи, известное как арбит-

ражное решение Неша.

Арбитражное решение представляет собой некую систему требований (аксиом), с помощью которых для любой игры выделяется ее единственное решение — оптимальный исход этой игры.

Пусть vA и vB — цены матричных игр с матрицами A и B соответственно. Тогда в явном виде арбитражное решение Нэша для пары (H1 , H2 ) — это точка (H1* , H2* ) , для которой произве-

дение (функция полезности):

U = (H1 - vA )×(H2 - vB )

(3.10)

достигает своего наибольшего значения в той части областиD возможных исходов биматричной игры, в которой выполняются условия:

H1 ³ vA , H2 ³ vB .

В качестве иллюстрации решения кооперативной игры рассмотрим следующую задачу.

№ 3.5. Оптимальное распределение прибыли. Имеются две фирмы: первая может произвести одно из двух изделий А1 и А2 , вторая — одно из трех изделий В1 , В2 и В3 . Если первая фирма

произведет продукцию Ai ,i =1,2 , а вторая — B j , j =1,3 , то при-

быль этих фирм(зависящая от того, являются ли эти изделия взаимодополняющими или конкурирующими), определяется таблицей 3.1:

			Т а б л и ц а 3 . 1
	В1	В2	В3
А1	[3,3]	[0, 0]	[4,1]
А2	[2, 0]	[1,5]	[2, 2]

73

Считая, что фирмы заключают между собой соглашение, определить справедливое распределение прибыли, спользуя арбитражное решение Нэша.

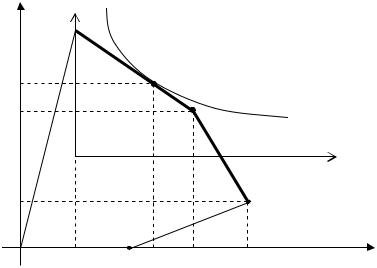
Решение. Построим в декартовой системе координат многоугольник D возможных исходов игры, вершинами которого являются возможные исходы игры, приведенные в таблице 3.1:

H2 H2¢

5 M

4			M *
H2*
3			N				U = U *
2							H1¢
	0¢
1
				4
0	1		2 H1* 3		5		H1

Рис. 3.7

Выделим в этом многоугольнике множество Паретооптимальных решений (северо-восточную границу).

Вычислим цены игры для матричных игр:

æ 3	0	4 ö	и	æ 3			0	1	ö	,
A = ç	1	÷		B = ç			5	2	÷
è 2		2 ø		è0					ø
а именно,	vA =1,		vB	=	15	.	Следовательно, функция полезности
				8

по Нэшу примет вид:

74

U = (H1 -1)×çæ H2 -		15	÷ö .
è	8		ø
Введем новую систему координат O¢H1¢H2¢ параллельным пе-
реносом начала	координат в точкуO¢çæ1,			15	÷ö . По рисунку 3.7
			è 8		ø

видно, что оптимальным решением задачи(U ® max ) является

точка касания функции полезности с отрезкомMN . Определим уравнение этой прямой, как уравнение прямой, проходящей

		æ		25 ö			æ		9 ö		в системе O¢H1¢H2¢ .
	через две данные точки	M ç	0,		÷	и	N ç	2,		÷
				8					8
		è			ø		è			ø

Получим следующее уравнение: 8H1¢ + 8H2¢ = 25 .

Чтобы определить координаты оптимальной точкиM * , решим следующую оптимизационную задачу: Найти максимум целевой функции

U = H1¢ × H2¢ ® max ,

при условии, что

8H1¢ + 8H2¢ = 25 .

Построим функцию Лагранжа:

L (H1¢, H2¢, l) = H1¢H2¢ + l (25 - 8H1¢ -8H2¢ ).

Вычислив частные производные первого порядка и приравняв их к нулю, получим следующую систему уравнений:

ìH2¢ -8l = 0; ïíH1¢ -8l = 0;

ïî25 - 8H1¢ -8H2¢ = 0,

75

решение которой имеет вид:

H1¢ = 25 , H2¢ = 25 . 16 16

Перейдя к старым координатам, получим:

			25	41			25		15			55
	H1	=		+1 =	, H=	2		+			=			.
			16				16		8			16
				16

Для определения оптимальной смешанной стратегии в этой кооперативной игре, реализующей полученный результат, надо

смешать ситуации (3, 3)						и (1, 5)				в некоторой пропорции так,
чтобы выполнялось равенство:
p ×(3,3 )+			1(- p)× (1,5			=) çæ	41	,	55	÷ö .
						è16 16				ø
Решив последнее уравнение, получим:
p =	25	,	1- p =	7	.
32			32

Следовательно, для получения «справедливой» доли, фирмы

должны воспроизводить ситуацию (3, 3) — с частотой 25 , а си32

туацию (5, 1) с частотой 7 , а остальные ситуации не воспроиз32

водить совсем. При этом средний выигрыш первого игрока

составит 41 у.е., а второго — 55 у.е. 16 16

76

s Вопросы для самоконтроля

1.Дайте определение биматричной игры.

2.В чем, на Ваш взгляд, состоит основная сложность биматричной игры?

3.Какая теорема отвечает на вопрос о существовании равновесной ситуации в биматричной игре? Приведите ее формулировку.

4. Каким соотношением определяется ситуация равновесия

в биматричной игре?

5.Могут ли функции выигрышей игроков достигать максимума одновременно?

6.Чем в равновесной ситуации определяется выигрыш игрока?

7.В чем отличие антагонизма интересов от антагонизма поведения?

8.Какие игры называются кооперативными?

9.Какова основная цель объединения игроков в коалиции?

10.В чем заключается особенность биматричной игры?

11.Какие допущения необходимо сделать для нахождения оптимального исхода в кооперативной игре?

12.Что такое «арбитражное решение Нэша»?

13.Что произойдет, если в процессе игры игроки разорвут коалицию? Возможно ли это?

77