10.3.Метод золотого сечения.

На каждом шаге, за исключением первого, вычисление значения функции f(x) производится лишь один раз. Эта точка называется золотым сечением и выбирается специальным образом.

Геометрическая идея метода:

На первом шаге процесса оптимизации внутри отрезка [a₀, b₀] выбирают две внутренние точки x₁ и x₂ и вычисляют значения целевой функции f(x₁) и f(x₂). Так как в данном случае f(x₁) < f(x₂), то очевидно, что минимум расположен на одном из прилегающих к x₁ отрезков [a₀, x₁] или [x₁, x₂]. Поэтому отрезок [x₂,b₀] можно отбросить, сузив тем самым первоначальный интервал неопределенности.

Второй шаг проводится на отрезке [a₁, b₁], где a₁ = a₀ и b₁ = x₂. Нужно снова выбрать две внутренние точки, но одна из них (x₁) осталась из предыдущего шага, поэтому достаточно вычислить лишь одну точку x₃, вычислить значение f(x₃) и провести сравнение. Так как здесь f(x₃) > f(x₁), то ясно, что минимум находится на отрезке [x₃, b₁]. Этот отрезок можно обозначить [a₂, b₂], снова выбрать одну внутреннюю точку и повторить процедуру сужения интервала неопределенности. Процесс оптимизации повторяется до тех пор, пока длина очередного отрезка [a_n, b_n] не станет меньше заданной величины .

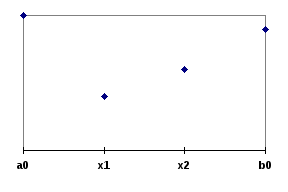
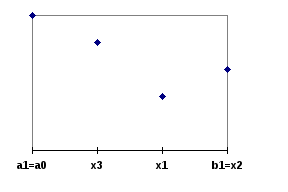
Вывод соотношения золотого сечения:

Пусть длина интервала неопределенности равна l, а точка деления делит его на части l₁, l₂ : l₁ > l₂, l = l₁ + l₂ .Золотое сечение интервала неопределенности выбирается так, чтобы длины большего отрезка к длине всего интервала равнялось отношению длины меньшего отрезка к длине большего отрезка:

Из этого соотношения можно найти точку деления, определив отношение l₂/l₁ .Для этого

l₁² = l₂ * l  l₁² = l₂ * (l₁ + l₂)

l₂² + l₁ * l₂ - l₁² = 0



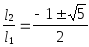
Так как интерес представляет только положительное решение, то

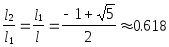
Отсюда l₁  0.618*l, l₂  0.382*l .

На первом шаге исходный интервал неопределенности равен d₀ = b₀ - a₀ .При этом x₁ - a₀ = b₀ - x₂ = 0.382*d₀ и b₀ - x₁ = x₂ - a₀ = 0.618*d₀ .

После первого шага оптимизации получается новый интервал неопределенности d₁ = b₁ - a₁ = x₂ - a₀ = 0.618*d₀ .

После второго шага оптимизации имеем d₂ = b₂ - a₂ = b_1­ - x₃ = 0.618*d₁ = 0.618² * d₀ .

Используя полученные соотношения, можно записать координаты точек деления y и z отрезка [a_k,b_k] на k+1 шаге оптимизации (y < z):

y = 0.618*a_k + 0.382*b_k : z = 0.382*a_k + 0.618*b_k .

При этом длина интервала неопределенности равна

d_k = b_k - a_k = 0.618^k * d₀ .

Процесс оптимизации заканчивается при выполнении условия d_k <  .При этом искомая величина лежит в интервале a_k < x_opt < b_k. В качестве оптимального значения можно принять x_opt = a_k (или x_opt = b_k или x_opt = (a_k + b_k)/2 ).

10.4.Метод координатного спуска.

10.5.Метод наискорейшего спуска.

1. Выбор вектора начальных приближений и вычисление значения целевой функции в этой точке (). Выбор величины шага.

2. Вычисление нормированного вектора-градиента в этой точке.

3. Определение направления поиска по формуле

4. Поиск любым методом одномерного поиска точки , в которой функция имеет минимальное значение ().

5. Если выполняется условие:

,

то поиск прекращается и выводят полученные результаты. В противном случае выполняют этап 6.

6. За новое начальное приближение принимают найденную на этапе 4 точку (=,=) и расчеты повторяют с пункта 2.

Выделить особенность метода: если первый же шаг из очередной начальной точки неудачен (функция возрастает), то, как правило, уменьшают шаг, т.е. h^(k+1) = h^(k) /z, где z > 1 . Условие окончания поиска при этом может быть записано в виде h^(k) <  .