Краткий курс математического анализа. Том 2

100Гл. 4. Дифференциальное исчисление функций многих переменных

40.4.Свойства якобианов отображений. Напомним, что отображение f множества X Rm в пространство Rn задается n функциями от m переменных:

	y1 = f1(x1, ..., xm),
y = f (x) =	. . . . . . . . . . . . .	(40.35)
	yn = fn(x1, ..., xm),
x = (x1, ..., xm) X, y = (y1, ..., yn) Rn.

Функции f называются координатными функциями отображения f , j = 1, 2, ..., n.

Если X — открытое множество, то отображение (40.35) называется

дифференцируемым в точке этого множества, если в нем дифференцируемы все координаты функции. Отображение (40.35) непрерывно дифференцируемо на множестве X, если все координатные функции

fi, i = 1, 2, ..., n, непрерывно дифференцируемы на X (т. е. имеют на X непрерывные производные).

Пусть y = f (x) — непрерывно дифференцируемое отображение открытого множества X Rm в открытое множество Y Rn, а z = g(y) —

непрерывно дифференцируемое отображение открытого множества Y в пространство Rp, x = (x1, ..., xm), y = (y1, ..., yn), z = (z1, ..., zp). Тог-

да имеет смысл композиция								g ◦ f отображений f и g и она также
непрерывно дифференцируема.
Согласно правилу дифференцирования сложных функций
			n
	∂zi	=		∂zi		∂yk	,	i = 1, 2, ..., p, j = 1, 2, ..., m.
	∂xj		k=1	∂yk ∂xj

Это означает в силу правила умножения матриц, что при компо-

зиции отображений их матрицы Якоби перемножаются:
∂xj		=	∂yk		∂xj .		(40.36)
	∂zi			∂zi		∂yk

Если m = n = p, то, поскольку при умножении матриц их определители также перемножаются, из равенства (26.36) следует равенство

=∂(z1, ..., zn ) ∂(y1, ..., yn) , (40.37) ∂(x1, ..., xn) ∂(y1, ..., yn) ∂(x1, ..., xn)

т.е. при композиции отображений их якобианы перемножаются. Если отображение z = g(y) является обратным к взаимно

однозначному отображению y = f (x), то отображение g(f (x)) = = f −1(f (x)) = x является тождественным отображением:

z1 = x1, ..., zn = xn

§ 40. Неявные функции. Отображения

101

и его якобиан, очевидно, равен 1. Поэтому равенство (40.37) в этом случае принимает вид

∂(x1	, ..., xn)		∂(y1	, ..., yn)		= 1.	(40.38)
∂(y1	, ..., yn)		∂(x1	, ..., xn)

Отсюда следует, что если отображение y = f (x) непрерывно дифференцируемо, взаимно однозначно и имеет якобиан, не равный нулю, то обратное отображение y = f −1(y) также имеет якобиан, не равный

нулю, и		, ..., xn)				1
	∂(x1		=					.	(40.39)
	∂(y1	, ..., yn)			∂(y1	, ..., yn)
					∂(x1	, ..., xn)

Формулы (40.38) и (40.39) показывают, что при композиции отображений их якобианы ведут себя в определенном смысле аналогично производным функций одной переменной.

40.5. Непрерывно дифференцируемые отображения. Для функций одной переменной имеется простое достаточное условие обратимости дифференцируемой функции на промежутке, т. е. условие существования у нее однозначной обратной функции — этим условием является неравенство нулю ее производной. Но уже даже для отображений плоских областей нет аналогичного простого признака существования однозначного обратного отображения. Тем не менее можно указать условие локальной обратимости отображения, т. е. его обратимости в достаточно малой окрестности точки.

Пусть X Rm и f — отображение множества X в пространство Rn.

О п р е д е л е н и е 1. Взаимно однозначное отображение, у кото-

рого как оно само, так и ему обратное отображение непрерывны, называется гомеоморфным отображением или гомеоморфизмом.

Например, непрерывная строго монотонная на отрезке функция задает его гомеоморфное отображение (см. теорему 3 в п. 7.3).

О п р е д е л е н и е 2. Отображение называется (непрерывно) дифференцируемым, если его координатные функции (непрерывно) диф-

ференцируемы.

Поскольку понятие дифференцируемости функции в точке определено лишь для функций, заданных в окрестности этой точки, то определение (непрерывно) дифференцируемого отображения применимо лишь к отображению открытого множества.

Очевидно, что дифференцируемое отображение непрерывно, так как дифференцируемые функции непрерывны (см. теорему 1 в п. 36.2). Непрерывно также и непрерывно дифференцируемое отображение, т. е. отображение, координатные функции которого имеют непрерывные частные производные (см. п. 36.2), так как непрерывно дифференцируемые функции дифференцируемы (см. там же теорему 3).

102Гл. 4. Дифференциальное исчисление функций многих переменных

Вдальнейшем будем предполагать, что множества, на которых заданы рассматриваемые отображения, являются открытыми множествами.

О п р е д е л е н и е 3. Гомеоморфное отображение, у которого как

оно само, так и ему обратное непрерывно дифференцируемы, называется диффеоморфным отображением или диффеоморфизмом.

Например, диффеоморфизмом является отображение интервала числовой прямой, задаваемое непрерывно дифференцируемой на нем функцией с производной, не равной нулю.

О п р е д е л е н и е 4. Отображение называется локально гомеоморфным (локально диффеоморфным) в точке, если у этой точки

и у ее образа существуют окрестности, гомеоморфно (диффеоморфно) отображающиеся друг на друга при данном отображении.

Ясно, что локально диффеоморфное в данной точке отображение является и локально гомеоморфным в этой точке.

Отметим, что образ открытого множества при локально гомеоморфном во всех точках отображении является также открытым множеством. Это следует из того, что у каждой точки образа отображаемого открытого множества имеется окрестность, являющаяся образом окрестности прообраза рассматриваемой точки. Иначе говоря, у каждой точки образа открытого множества имеется окрестность, содержащаяся в образе этого множества, что и означает его открытость.

Заметим еще, что если окрестность U точки x(0) гомеоморфно (диффеоморфно) отображается на окрестность V точки y(0) = f (x(0)), то и любая окрестность U1 U точки x(0) гомеоморфно (диффеоморфно) отображается на некоторую окрестность V1 точки y(0). Действительно, образ V1 = f (U1) открытого множества U1 при отображении f является в силу вышесказанного открытым множеством, содержащим точку y(0), т. е. ее окрестностью.

Отсюда следует, что если отображение f локально гомеоморфно (диффеоморфно) в точке x(0), то существуют сколь угодно малые по диаметру окрестности этой точки, гомеоморфно (диффеоморфно) отображающиеся на окрестность точки y(0) = f (x(0)). При этом эти окрестности можно выбрать линейно связными, т. е. такими, чтобы они являлись областями: для этого, например, достаточно выбрать шаровую окрестность точки x(0).

За м е ч а н и е 1. На окрестностях U и V соответственно точек x(0)

иy(0) = f (x(0)), указанных в определении локального диффеоморфизма в точке x(0), отображение f на U и обратное отображение f −1 на V имеют не равные нулю якобианы.

Это сразу следует из того, что согласно формуле (40.38) произве-

дение этих якобианов равно единице.

Пусть G — открытое в пространстве Rxn множество и f : G → Ryn.

§ 40. Неявные функции. Отображения

103

Т е о р е м а 3. Если у непрерывно дифференцируемого отображения f в некоторой точке якобиан не равен нулю, то в этой точке отображение локально диффеоморфно.

С л е д с т в и е 1. Непрерывно дифференцируемое отображение с якобианом, не равным нулю, отображает открытое множество

воткрытое.

Сл е д с т в и е 2 (принцип сохранения области). Образ области при непрерывно дифференцируемом отображении с якобианом, не равным нулю, является областью.

Пусть G — открытое множество в пространстве Rxn,										y = f (x) —
непрерывно дифференцируемое отображение G в пространство Ryn,
x = (x1, x2, ..., xn), y = (y1, y2, ..., yn), f : G → Ryn, пусть fi — коорди-
натные функции отображения f , i = 1, 2, ..., n:
					y1 = f1(x1, x2, ..., xn),
							, x2, ..., xn),
	y = f (x) =			y2 = f2(x1						(40.40)
и				. . . . . . . . . . . . . . .
				yn = fn(x1, x2, ..., xn),
		∂(f ,	,	, f )
		1 f2	... n			x(0) = 0,	x	(0)	G.	(40.41)
		∂(x1, x2	, ..., xn)
	Введем обозначения

Fi(x, y) = fi(x1, x2, ..., xn) − yi, i = 1, 2, ..., n,	(40.42)
y(0) = f (x(0)).	(40.43)

Тогда условие y = f (x) означает, что x и y являются решениями системы уравнений

				Fi(x, y) = 0, i = 1, 2, ..., n.										(40.44)
Если				F (x, y) = (F1(x, y), ..., Fn(x, y)),
то систему (40.40) можно записать в виде
								F (x, y) = 0,						(40.45)
что, согласно сказанному выше, равносильно условию
								y = f (x).						(40.46)
Из выполнения условий (41.41) следует, что
	∂(F1, F2, ..., Fn)							=	0	∂(f1, f2, ..., fn)		=	0.	(40.47)
2		...			y		)	(40.43)	2 ...			(40.41)
	∂(x1, x ,		, xn)	(0),		(0)		(40.42)		∂(x1, x , , xn)	(0)

104 Гл. 4. Дифференциальное исчисление функций многих переменных

Поскольку (см. (40.42) и (40.43))

Fi(x0, y0) = 0, i = 1, 2, ..., n,

(40.48)

то, согласно теореме 2, существуют окрестности U точки x(0), V — точки y(0) и единственное отображение

x = g(y) такие, что

F (g(y), y) = 0, y V , g(y) U , (40.49)

или, что то же самое (см. (40.45) и (40.46)):

f (g(y)) = y, y V , g(y) U.	(40.50)
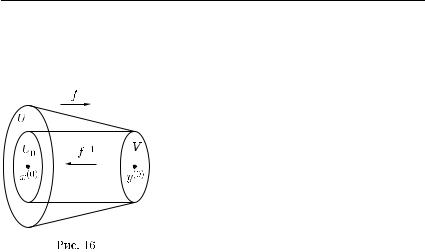
Пусть (см. рис. 16)
U0 = g(V ) U.	(40.51)

Если для какой-то точки x U имеет место включение y = f (x ) V , то в силу того, что g(y ) является единственным

решением уравнения y = f (x) при x U , то из равенств y = f (x ) и y = f (g(y )) имеем x = g(y ) и, следовательно, x g(V ) = U0.

Иначе говоря, точка x из окрестности U точки x(0) может отображаться при отображении f , рассматриваемом лишь на множестве U , только в том случае, когда x U0. Это означает, что для непрерывного отображения f , рассматриваемого только на открытом множестве U , множество U0 является прообразом открытого множества V. Поэтому множество U0 является открытым множеством (см. теоре-

му 5 в п. 35.3).

В силу условия y(0) = f (x(0)) V , x(0) U , имеем x(0) U0 и, следовательно, множество U0 является окрестностью точки x(0).

Таким образом отображение f отображает окрестность U0 точки x(0) на окрестность V точки y(0), а отображение g отображает окрестность V на U0:

f (U0) = V , g(V ) = U0,

и для всех y V имеет место равенство

f (g(y)) = y.

Это означает, что отображения f и g взаимно обратны: f = g−1, g = f −1.

Наконец, согласно теореме 2 отображение f −1 = g непрерывно дифференцируемо на V. Однозначность обратного отображения f −1 на V = f (U0) означает, что отображение f : U0 → V взаимно однозначно отображает U0 на V.

Итак, непрерывно дифференцируемое отображение f взаимно однозначно отображает некоторую окрестность точки x(0) на окрест-

§ 41. Условный экстремум

105

ность точки y(0), причем обратное отображение также непрерывно дифференцируемо. Это и означает локальную диффеоморфность отображения f в рассматриваемой точке.

Первое следствие из теоремы вытекает из того, что локально диффеоморфное отображение локально гомеоморфно, а при локально гомеоморфном отображении открытое множество, как это было отмечено выше, отображается в открытое.

Поскольку область есть линейно связное открытое множество и непрерывный образ линейно связного множества есть также линейно связное множество (теорема 3 в п. 35.2), то второе следствие вытекает из первого.

За м е ч а н и е 2. Как видно из доказательства теоремы, при выполнении ее условий обратное отображение fU−01 к сужению fU0 отображения f на множестве U0 не только дифференцируемо на множестве V , но и непрерывно дифференцируемо на нем.

За м е ч а н и е 3. Условие того, что якобиан не равен нулю в рассматриваемой точке открытого множества, существенно для справед-

ливости утверждения доказанной теоремы. Действительно, например, уже для случая n = 1 функция f (x) = x2 отображает открытое мно-

жество (−1, 1) в неоткрытое [0, 1) (здесь якобианом является производная и f (0) = 0).

З а м е ч а н и е 4. Было доказано, что однозначное обратное отображение для отображения с неравным нулю якобианом существует только локально, т. е. в окрестности каждой точки. В целом отображение с неравным нулю якобианом не имеет, вообще говоря, однозначного обратного отображения.

Покажем это на примере отображения w = z2, z C, w C, единичного круга с выколотым центром: 0 < |z| < 1, которое отображает

это множество на себя. Это отображение не взаимно однозначно,
так как обратное отображение z = √				двузначно: для любого w,
			w
0 < w	< 1,	существуют два значения корня			z = √		, 0 < z	< 1.	Пока-
						w
| |					| |

жем, что якобиан этого отображения не равен нулю. Пусть z = x + iy, w = u + iv, тогда u + iv = (x + iy)2, а потому u = x2 − y2, v = 2xy.

Отсюда

∂(u, v)	=		2x	2y		= 4(x2 + y2) = 0 при z = 0.
∂(x, y)		2y		−2x

§41. Условный экстремум

41.1.Прямой метод отыскания точек условного экстремума. Пусть на множестве X Rn задано m + 1 функций f0, f1, ...

..., fm, и пусть X0 — подмножество множества X, на котором послед-

106 Гл. 4. Дифференциальное исчисление функций многих переменных

ние m функций одновременно обращаются в нуль:

X0 = {x X : f1(x) =		... = fm(x) = 0}.
Уравнения
f1(x) = 0,	...,	fm(x) = 0	(41.1)
называются уравнениями связи.	x(0) X0 называется точкой услов-
О п р е д е л е н и е 1. Точка

ного или относительного экстремума функции f0 при выполнении условий связи (41.1), если она является точкой обычного экстремума сужения функции f0 на множестве X0.

Точка условного экстремума может быть либо точкой условного (строгого) максимума, либо точкой

условного (строгого) минимума. Если x(0) — точка условного экс-

тремума функции f0, то говорят, что функция f0 имеет в этой точке условный экстремум.

П р и м е р. Рассмотрим функцию f (x, y) = y2 − x2 (рис. 17). Она не

имеет обычных экстремумов.

При уравнении связи y = 0 имеем f (x, 0) = −x2. Эта функция имеет максимум при x = 0. Следовательно, точка (0, 0) является точкой услов-

ного экстремума функции f (x, y) = y2 − x2 при уравнении связи x = 0.

Если в качестве

уравнения

связи взять

уравнение

y = x + 1,

то

f (x, x + 1) = (x + 1)2

−

x2 = 2x + 1. Эта функция не имеет экс-

2

− x

2

не имеет условного

тремумов. Поэтому функция f (x, y) = y

экстремума при уравнении связи y = x + 1.

Метод, примененный при решении этой задачи, можно применить

и в общем случае для изучения условного экстремума.

Пусть все функции f0, f1, ..., fm

непрерывно дифференцируемы

в некоторой окрестности точки

x(0),

f1,

f ,

...

,

f

а градиенты (0)

,

2

m

последних m функций линейно независимы в точке x

или, что то

же самое, ранг матрицы Якоби

∂f1

...

∂f1

∂x1

∂xn

(41.2)

. . . . . . . . .

∂fm

...

∂fm

∂x1

∂xn

равен m (отсюда, очевидно, следует, что m n, так как ранг матрицы не может быть больше числа ее столбцов).

Равенство ранга матрицы (41.2) числу m равносильно существованию у нее минора порядка m, не равного нулю.

§ 41. Условный экстремум

107

Пусть для определенности

∂(f , ..., f )

∂(x1, ..., xm ) x(0) = 0

иn > m. Тогда, согласно теореме о неявных функциях, система урав-1 m

нений (41.1) в некоторой окрестности U точки	x(0) = (x1(0), ..., xn(0))
в пространстве Rn переменных x1, ..., xn равносильна заданию m
функций
x1 = ϕ1(xm+1, ..., xn),	(41.3)
. . . . . . . . . . . . . . .
xm = ϕm(xm+1, ..., xn)

в некоторой окрестности U точки x(0) = (xm(0)+1, ..., xn(0)) в простран-
стве Rn−m	переменных	(xm+1, ..., xn).	U = U (x(0))		U =
				и
Иначе говоря, существуют такие окрестности

= U (x(0)) точек x(0) и x(0) соответственно в пространствах Rn и Rn−m,

что точка

x = (x1

,

...

, x

)

U

удовлетворяет

условию

(41.1)

тогда

n

),

и

только тогда, когда она имеет вид (ϕ1

(x),

, ϕ

(x),

x

1,

...

, x

...

m

m+

n

, ..., xn) U .

x = (xm+1

f

(x),

x = (xm+1

, ..., x

),

как результат под-

Определим функцию

0

n

становки выражений

(41.3) для переменных x1, ..., xn в y = f0(x1, ...

..., xn), т. е.

0

def

(xm+1, ..., xn) = f0(ϕ1(x), ..., ϕm(x), xm+1, ..., xn).

f0

(x) = f0

ки x(0).

точ-

Функция f (x)

определена в вышеуказанной окрестности

U

Ввиду равносильности условий (41.1) и (41.3) точка x(0) является точкой условного экстремума для функции f0 при выполнении уравнений связи (41.1) тогда и только тогда, когда точка x(0) является точкой обычного экстремума для функции f0.

Затруднение при практическом использовании изложенного метода сведения задачи отыскания точек условного экстремума к задаче отыскания точек обычного экстремума состоит в том, что решение системы уравнений (41.1) не выражается через элементарные функции даже во многих простейших случаях. В следующем пункте будет изложен метод отыскания точек условного экстремума, значительно более удобный для применения.

41.2. Метод неопределенных множителей Лагранжа. Те о- р е м а 1. Пусть функции f0, f1, ..., fm непрерывно дифференцируемы в окрестности точки x(0) Rn, n > m. Если x(0) является точкой условного экстремума функции f0 относительно уравнений связи (41.1), то в этой точке градиенты f0, f1, ..., fm линейно

108 Гл. 4. Дифференциальное исчисление функций многих переменных

зависимы, т. е. существуют такие числа λj , j = 0, 1, ..., m, одновременно не равные нулю, что

λ0 f0 + λ1 f1 + ... + λm fm = 0.

(41.4)

С л е д с т в и е. Если в точке x(0) условного экстремума функции f0 относительно уравнений связи (41.1) градиенты f1, ..., fm линейно независимы, то существуют такие числа λ1, ..., λm, что

	f0 + λ1 f1 + ... + λm fm = 0,				(41.5)
или, в координатной форме,
		m
	∂f0		∂fk
		+ λk		= 0, i = 1, 2, ..., n.	(41.6)
	∂xi	k=1	∂xi

Существование множителей λ0, λ1, ..., λm в теореме 1 (соответственно множителей λ1, ..., λm в ее следствии) является необходимым условием для точки относительного экстремума x(0) функции f0 при выполнении уравнений связи (41.1).

Если градиенты f1, ..., fm линейно независимы, то функция

F (x) = f0(x) + λ1f1(x) + ... + λmfm(x),

(41.7)

где числа λ1, ..., λm удовлетворяют условию (41.5), называется функцией Лагранжа, а сами числа λ1, ..., λm — множителями Лагранжа.

Условие (41.6) означает, что F = 0, или, в координатной записи,

	∂F (x(0))	= 0, i = 1, 2, ..., n,
	∂xi
иначе говоря,
	dF (x(0)) = 0.		(41.8)

Таким образом, точка x(0) является стационарной точкой функции Лагранжа.

Пусть точка x(0) = (x(10), ..., x(n0)) удовлетворяет уравнениям связи (41.1):

fk(x(0)) = 0, k = 1, 2, ..., m

(41.9)

и в ней градиенты f0, f1, ..., fm линейно независимы. Покажем, что в этом случае точка x(0) не может быть точкой условного экстремума.

§ 41. Условный экстремум

109

Если градиенты f0, f1, ..., fm линейно независимы в точке x(0), то в этой точке ранг матрицы

		∂f0		...	∂f0
		∂x1			∂xn
		∂f1			∂f1
		∂x1		...	∂xn		(41.10)
				...
. . . . . . . . .
	∂fm				∂fm
		∂x1			∂xn

равен m + 1 и, следовательно, у этой матрицы существует минор порядка m + 1, не равный нулю. Пусть для определенности этим минором будет минор, образованный первыми m + 1 столбцами мат-

рицы (41.10), т. е.		∂(f0, f1, ..., fm)	x(0) = 0.
				(41.11)
		∂(x1, x2, ..., xm+1)
Рассмотрим отображение
y0	= f0(x1, ..., xm+1, xm(0)+2, ..., xn(0)),
y1	= f1(x1, ..., xm+1, xm(0)+2, ..., xn(0)),			(41.12)
. . . . . . . . . . . . . . . . . . . . . . . . .

ym = fm(x1, ..., xm+1, x(m0)+2, ..., x(n0)).

Поскольку x(0) удовлетворяет уравнениям связи (41.1) (см. (41.9)),

то для нее имеем

f0(x(10), ..., x(n0)) = f0(x(0)),

f1(x(10), ..., x(n0)) = 0,

. . . . . . . . . . . . . . . . .

fm(x(10), ..., x(n0)) = 0,

т. е. отображение (41.12) отображает точку (x1(0), ..., xm(0)+1) в точку
(f0	(x(0)), 0, ..., 0).
			!		"

mраз

Всилу же условия (41.11) отображение (41.12) отображает лю-

бую достаточно малую окрестность U точки (x(10), ..., x(m0)+1) в пространстве переменных x1, ..., xm+1 на некоторую окрестность V точки (f0(x(0)), 0, ..., 0) (п. 40.5). Поэтому для всех достаточно малых η > 0, а именно таких, что (f0(x(0)) ± η, 0, ..., 0) V , отображение (41.12) отображает в точки

(f0(x(0)) + η, 0, ..., 0) и (f0(x(0)) − η, 0, ..., 0)

какие-то точки

(x1, ..., xm+1) и (x1 , ..., xm+1)