Краткий курс математического анализа. Том 2

120 Гл. 5. Интегральное исчисление функций многих переменных

он пересекается с X1, следует, что он пересекается и с X2. Поэтому, согласно определению (42.6),

μsk(X1) μsk(X2), μSk(X1) μSk(X2).

(42.26)

Перейдя в этих неравенствах к пределу при k → ∞, получим неравенства (42.24) и (42.25).

Докажем следствие. Если X1 X2	и μX2 = 0, то
0 μ X1 μ X2	= μX2 = 0,
(42.15) (42.25)	(42.16)

т. е. μ X1 = 0, и, следовательно, согласно замечанию 1 множество X измеримо, и его мера равна нулю.

Изучим теперь связь между измеримостью множества и мерой его границы. Предварительно сделаем несколько замечаний.

З а м е ч а н и е 5. Любое объединение конечного или бесконечного множества кубов данного ранга является замкнутым множеством.

Пусть {Qi} — конечное или бесконечное множество кубов данного ранга k,

и x				X = i		Qi	(42.27)
		X	. Любая ограниченная окрестность точки x (как и вообще
				n	) пересекается лишь с конечным мно-
любой точки пространства R

жеством кубов ранга k и, следовательно, с конечным множеством
слагаемых Qij , j = 1, 2, ..., m, суммы i		Qi. Поэтому
	j
	m		(42.28)
x =1 Qij .

Поскольку кубы Qj являются замкнутыми множествами и объединение конечного множества замкнутых множеств снова есть замкнутое множество, то

j
m		m
Qij =		Qij .	(42.29)
=1		j=1

Таким образом,

x m Qij

j=1

и, следовательно, существует такой номер j0, что x Qij0 , а поэтому

в силу равенства (42.27) x X. Таким образом, из включения x X вытекает, что x X. Это означает, что X = X, т. е., что X — замкнутое множество.

Для всякого множества X Rn обозначим σk = σk(X) объединение кубов ранга k, содержащихся в множестве Sk = Sk(X), но не содер-

§ 42. Кратные интегралы

121

жащихся в множестве sk = sk(X) (см. заштрихованный квадрат на рис. 19, n = 2):

def	Q.	(42.30)
σk = σk(X) =
Q Tk
Q Sk , Q /sk
Из этого определения следует, что
Sk = sk σk,		(42.31)

причем никакой куб ранга k не принадлежит одновременно множествам sk и σk. Поэтому согласно определению (42.6)

μSk = μsk + μσk 1).

(42.32)

В силу определения (42.30) множество σk так же, как и множества sk и Sk, является объединением кубов одного ранга, поэтому все эти множества являются замкнутыми множествами (см. замечание 5):

sk = sk,	S	k = Sk,		k = σk.	(42.33)
			σ

Напомним, что для любого множества X Rn имеют место равенства (см. 33.44))

X

= Xint ∂X, Xint ∩ ∂X = ,

(42.34)

где Xint — множество внутренних точек множества X, а ∂X — его граница.

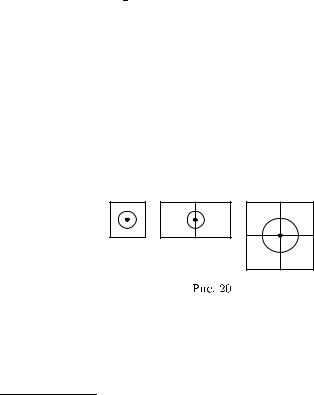
З а м е ч а н и е 6. Для любого многогранника S, состоящего из конечного или бесконечного множества кубов одного и того же ранга k, его точка имеет окрестность, содержащуюся в S, в том и только том случае, когда все кубы ранга k, содержащие точку x, содержатся в многограннике S (рис. 20).

Действительно, пусть x Sint и существует такой куб Q ранга k, что x Q и Q S. Тогда все внутренние точки этого куба не принадлежат многограннику S (его граничные точки, конечно, могут принадлежать S). Из того, что x Q следует, что любая окрестность точки x содержит внутреннюю точку куба Q, т. е. точку, не принад-

1) Меры μsk , μSk и μσk могут быть как конечными, так и бесконечными, причем, как обычно, для любого действительного числа a считается, что (+∞) + a = a + (+∞) = +∞ и (+∞) + (+∞) = +∞.

122 Гл. 5. Интегральное исчисление функций многих переменных

лежащую многограннику S. Таким образом x Sint — противоречие. Следовательно, все кубы ранга k, содержащие точку x S, содержатся в многограннике S.

Наоборот, пусть все кубы ранга k, содержащие точку x S, содер-

жатся в многограннике S. Допустим, что x 1 Sint. Тогда существует
такая последовательность точек x(m) U x;		, что x(m) Sint, m =
	m
= 1, 2, .... Окрестность U (x; 1) пересекается лишь с конечным множе-

ством кубов ранга k. Поэтому среди них имеется по крайней мере один куб Q, содержащий бесконечное множество членов последователь-

ности

{

x(m)

}

, а следовательно,

существует

подпоследовательность

x

(mi )

x

(m)

такая, что x

(mi )

Q, i = 1, 2, ..., n.

{

}

последовательности

{

}

1

Поскольку x(mi ) U

x;

, то ilim x(mi ) = x. Из того, что куб Q яв-

mi

→∞

Q. Но тогда согласно

ляется замкнутым множеством следует, что x

предположению Q

S,

и это противоречит тому, что куб

Q

содержит

(mi )

точки x

, не принадлежащие S. Следовательно, x Sint.

З а м е ч а н и е 7.

Наряду с равенством (42.31) имеет место более

точное равенство

Sk = (sk)int σk,

(42.35)

в котором слагаемые не пересекаются:

(sk)int ∩ σk = .

(42.36)

В силу формул (42.31) и (42.34) имеем

Докажем, что

Sk = (sk)int ∂sk σk.

(42.37)

∂sk σk.

(42.38)

Пусть x ∂sk. Поскольку

= s

X,

∂s

k

s

k

k

(42.33)

то x X и, следовательно, любой куб ранга k, содержащий точку x, содержится в множестве Sk (см. определение (42.9)). Согласно замечанию 6 хотя бы один куб Q из этих кубов не содержится в sk (в противном случае точка x являлась бы внутренней точкой множества sk, т. е. x (sk)int, а следовательно, не принадлежала бы его границе ∂sk). Таким образом, x Q Sk, Q sk.

В силу определения множества σk куб Q, а поэтому и точка x содержатся в σk. Это и означает справедливость включения (42.38). Из этого включения следует, что в равенстве (42.37) можно отбросить слагаемое ∂sk (оно входит в другое слагаемое), т. е. имеет место равенство (42.35).

Докажем теперь равенство (42.36). Если x (sk)int, то согласно замечанию 6 любой куб Q ранга k, содержащий точку x: Q x,

(42.33)

§ 42. Кратные интегралы

123

содержится в sk и, следовательно, не содержится в σk: Q σk. Это означает, что x / σk, т. е. имеет место равенство (42.36).

З а м е ч а н и е 8. Отметим еще (это нам вскоре пригодится), что если какой-то куб Q содержит как точки, принадлежащие некоторому множеству X, так и не принадлежащие ему, то этот куб Q содержит и граничные точки множества X. Пусть, например,

a Q ∩ X, b Q \ X.

Тогда, как в этом нетрудно убедиться, на отрезке [a, b] с концами в точках a и b существует такая точка ξ, что ξ ∂X. (Если на отрезке [a, b] ввести параметр t, например, так, чтобы [a, b] = {x = a + (b − a)t; 0 t 1}, и положить

t0 = sup t,

a+(b−a)t X

то ξ = a + (b − a)t0 ∂X.)

Поскольку же в силу выпуклости куба Q весь отрезок [a, b] содержится в Q, то ξ Q и, следовательно, пересечение куба Q с множеством ∂X непусто: оно во всяком случае содержит точку ξ.

Л е м м а 2. Для любого множества X Rn справедливы включения

∂X σk(X) Sk(∂X), k = 0, 1, ...,

(42.39)

(рис. 21).

Сначала докажем включение
∂X σk(X).	(42.40)

Пусть x ∂X. Заметив, что из включения X Sk(X) следует аналогичное включение для замыканий этих множеств

X Sk(X) = Sk(X),

124 Гл. 5. Интегральное исчисление функций многих переменных

получим

			=	(42.41)
x ∂X(42.34)X Sk(X)(42.35)sk(X)int σk(X).
Из включения же sk	(X)		X имеем
	42 9		)
		( .
		sk(X)int Xint.		(42.42)

Из включения же x ∂X следует, что точка x не является внутренней точкой множества X : x Xint (так как Xint ∩ ∂X = ). Поэтому

/	42 43
x(42.42)sk(X)int.	( . )

Из (42.41) и (42.43) вытекает, что точка x принадлежит множеству σk(X), т. е. включение (42.40) доказано.

Покажет теперь справедливость включения

σk(X) Sk(∂X).

(42.44)

Если x σk(X), то существует куб Q ранга k, содержащийся в множестве σk(X) и содержащий точку x: Q x. Согласно определению множества σk(X) этот куб принадлежит множеству Sk(X) и, следовательно, пересечение куба Q с множеством X не пусто. Поскольку этот куб согласно тому же определению не содержится в множестве sk(X), то он содержит и точки, не принадлежащие множеству X. Отсюда согласно замечанию 8 вытекает, что куб Q содержит точки границы ∂X множества X, а поэтому согласно определению множества Sk(∂X) как объединения всех кубов ранга k, пересекающихся с множеством ∂X, куб Q содержится в этом множестве. Итак, показано, что из условия x σk(X) следует, что x Sk(∂X), т. е. включение (42.44) также доказано.

Докажем теперь критерий измеримости по Жордану множества n-мерного пространства.

Те о р е м а 1. Для того чтобы множество X было измеримо по Жордану, необходимо и достаточно, чтобы оно было ограничено и чтобы его граница ∂X имела меру Жордана, равную нулю:

μ(∂X) = 0.

(42.45)

1. Покажем необходимость условий теоремы для измеримости множества. Если множество X Rn измеримо, то оно ограничено (заме-

чание 3), а пределы lim s	(X) = μ X и	lim Sk(X) = μ X, согласно
k→∞ k		k→∞

определению измеримости множества, конечны и равны между собой. Поэтому, заметив, что множество σk измеримо (см. замечание 4), следовательно,

μ σk = μσk, k = 0, 1, 2, ...,

(42.46)

§ 42. Кратные интегралы

125

и использовав монотонность верхней меры, будем иметь
0 μ ∂X μ σk	= μσk	= μSk	−	μsk	0	(42.47)
(42.40)	42 46	(42.32)			42 17
	( . )				( →. )

при k → ∞. Это означает, что μ (∂X) = 0. Отсюда, согласно замечанию 1, вытекает, что множество ∂X измеримо и что μ(∂X) = 0.

2. Докажем достаточность условий (42.45) для измеримости ограниченного множества. Пусть множество X Rn ограничено и μ(∂X) = 0. Тогда, согласно определению измеримости множества,

lim μSk(∂X) = 0.	(42.48)
k→∞

Из соотношения (42.32) с помощью включения (42.44) в силу мо-

нотонности меры имеем
0 μSk(X) μsk(X) = μσk(X) μSk(∂X)			0 (42.49)
−	42 32	(42.44)	42 48
	( . )		( →. )

при k → ∞.

Из ограниченности множества X вытекает существование конеч-

ных пределов (замечание 2) lim μSk(X) = μ X,		lim μsk(X) = μ X.
k	→∞	k	→∞

Поэтому, перейдя к пределу в неравенстве (42.49), получим

μ X = μ X,

т.е. множество X измеримо по Жордану.

За м е ч а н и е 9. Компакт, граница которого имеет меру нуль, является измеримым множеством.

Это сразу следует из теоремы 1, так как всякий компакт есть ограниченное множество.

За м е ч а н и е 10. Граница измеримого множества (как граница всякого ограниченного множества) является ограниченным множеством, а так как граница — замкнутое множество, то в данном случае она является компактом. Таким образом, согласно теореме 1 граница измеримого множества есть компакт меры нуль.

Л е м м а 3. Для любой пары множеств X и Y, лежащих в пространстве Rn, справедливы следующие вклю-

чения:
∂(X Y ) ∂X ∂Y ,	(42.50)
∂(X ∩ Y ) ∂X ∂Y ,	(42.51)
∂(X \ Y ) ∂X ∂Y ,	(42.52)

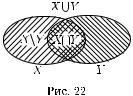
т. е. границы объединения, пересечения и разности двух множеств содержатся в объединении их границ (рис. 22).

Отсюда по индукции следует, что граница объединения и пересечения конечного числа множеств содержится в объединении их границ.

126 Гл. 5. Интегральное исчисление функций многих переменных

1. Докажем включение (42.50). Если x ∂(X Y ), то в любой окрестности точки x содержатся как точки, принадлежащие множеству X Y , так и точки, не принадлежащие ему. Возможны два случая: либо в любой окрестности точки x содержатся точки множества X, либо существует окрестность U0 точки x, не содержащая точек множества X. В первом случае в любой окрестности точки x имеются точки, как принадлежащие множеству X, так и не принадлежащие множеству X Y и, тем более, не принадлежащие множеству X. Это означает, что x ∂X.

Во втором случае какова бы ни была окрестность U точки x, окрестность U ∩ U0 этой точки, как и всякая ее окрестность, содержит точки множества X Y , причем в этом случае все они принадлежат множеству Y (так как U0 не содержит точек множества X) и содержит точки, не принадлежащие множеству X Y , а следовательно, не принадлежащие и множеству Y. Поскольку U ∩ U0 U , то в рассматриваемом случае в произвольной окрестности U точки x имеются как точки принадлежащие, так и не принадлежащие множеству Y. Это означает, что x ∂Y.

Итак, имеет место по крайней мере одно из включений x ∂X или

x ∂Y , т. е.

x ∂X ∂Y.

2.Докажем включение (42.51). Если x ∂(X ∩ Y ), то в любой окрестности точки x содержатся как точки, принадлежащие пересечению X ∩ Y (и, следовательно, точки множеств X и Y ), так и точки, не принадлежащие этому пересечению. Возможны два случая: либо

влюбой окрестности точки x имеются точки, не принадлежащие

множеству X, тогда x ∂X, либо существует окрестность U0 точки x, все точки которой принадлежат множеству X. Тогда для любой окрестности U точки x в ее окрестности U ∩ U0, как и во всякой окрестности этой точки, имеются точки, принадлежащие пересечению X ∩ Y , а следовательно, и множеству Y , и точки, не принадлежащие X ∩ Y , а поэтому не принадлежащие и множеству Y (ибо в U0 все точки принадлежат множеству X). Таким образом, в окрестности U ∩ U0

и, следовательно, в любой окрестности U точки x (ибо U U ∩ U0) имеются как точки, принадлежащие множеству Y, так и не принадлежащие ему. Это означает, что x ∂Y. Итак, если x ∂(X ∩ Y ), то

x ∂X ∂Y.

3.Докажем включение (42.52). Если x ∂(X \ Y ), то в любой

окрестности точки x содержатся как точки, принадлежащие разности X \ Y , так и не принадлежащие ей. Возможны два случая. Первый:

влюбой окрестности точки x содержатся точки, не принадлежащие множеству X, тогда в любой окрестности точки x имеются как точки, принадлежащие множеству X (так как имеются точки из X \ Y ),

§ 42. Кратные интегралы

127

так и не принадлежащие X. Поэтому в этом случае x ∂X. Второй случай: у точки x существует окрестность U0, все точки которой принадлежат множеству X. Тогда для любой окрестности U точки x в окрестности U ∩ U0 этой точки имеются как точки, принадлежащие разности X \ Y , а следовательно, не принадлежащие множеству Y , так и точки, не принадлежащие рассматриваемой разности, а поэтому принадлежащие множеству Y (ибо все точки из окрестности U0 принадлежат X). Поскольку U ∩ U0 U , то и в окрестности U содержатся как точки, принадлежащие множеству Y, так и не принадлежащие ему. Это означает, что x ∂Y. Таким образом, если x ∂(X \ Y ), то

x ∂X ∂Y.

Л е м м а 4 (полуаддитивность верхней меры). Для любой конечной совокупности множеств X1, X2, ..., Xm имеет место неравенство

	m
	i	(42.53)
μ m Xi	μ Xi.

i=1 =1

С л е д с т в и е. Объединение конечной системы множеств меры нуль также имеет меру нуль.

Каковы бы ни были множества X1, X2, ..., Xm, для любого ранга

k = 0, 1, 2, ... справедливо равенство
					m
		m	m
		Sk i=1 Xi	= i=1 Sk(Xi),
ибо, если куб Q пересекается с множеством					Xi, то он пересекается
хотя бы с одним множеством Xi,					i=1
			и наоборот. Поэтому
				m
m		m
μSk	Xi	= μ Sk(Xi) μSk(Xi).				(42.54)
i=1		i=1	(42.6) i=1

(Строгое неравенство получится в том случае, когда один и тот же куб Q ранга k будет входить в разные множества Sk(X). Это заведомо будет иметь место, если среди множеств Xi, имеются пересекающиеся.)

Заметив, что

m		m
k→∞ μSk i=1 Xi		= μ k=1 Xi	,
lim
lim μSk(Xi) = μ Xi,
k→∞

и перейдя в неравенстве (42.54) к пределу при k → ∞, получим неравенство (42.53).

128 Гл. 5. Интегральное исчисление функций многих переменных

Докажем следствие. Если μXi = 0, а следовательно, и μ Xi = 0, i = 1, 2, ..., m, то в силу неравенства (42.53) имеем

μ m Xi m μ Xi = 0.

i=1 i=1

Поэтому μ m Xi = 0, откуда, согласно замечанию 1 вытекает, что

i=1

m

множество Xi измеримо и его мера равна нулю.

i=1

Св о й с т в а м е р ы.

Св о й с т в о 1 (неотрицательность меры). Для любого измеримого множества X Rn всегда

μX 0.

Это сразу следует из (42.15) и (42.16).

С в о й с т в о 2 (монотонность меры). Если X1 и X2 — измеримые множества и X1 X2, то

μX1 μX2.

Это сразу следует из леммы 1 и определения (42. 16) меры измеримого множества.

С в о й с т в о 3. Объединение и пересечение конечного числа измеримых множеств, а также разность двух измеримых множеств являются измеримыми множествами.

В самом деле, если множества X1, X2, ..., Xm измеримы, то они ограничены, а поэтому ограничены их объединение и пересечение;

кроме того, их границы ∂Xi имеют меру нуль (теорема 1), следова-

m

тельно, и объединение ∂Xi их границ имеет меру нуль (следствие

i=1				объединения иmпере-
	m		m
леммы 4). Границы же ∂ i=1 Xi			и ∂ i=1 Xi
сечения множеств Xi, i = 1, 2, ..., m, содержатся в множестве					i
					∂Xi
					=1

(лемма 3) и потому также имеют меру нуль (следствие леммы 1).

m m

Поэтому сами эти множества

Xi и

Xi являются измеримыми

i=1 i=1

множествами (теорема 1).

Аналогично доказывается измеримость разности измеримых множеств.

Из свойства 3 меры и леммы 4, очевидно, следует, что для любых измеримых множеств Xi, i = 1, 2, ..., m, справедливо неравенство

	m
	i
m
μ Xi μXi.		(42.55)

i=1 =1

§ 42. Кратные интегралы

129

С в о й с т в о 4 (конечная аддитивность меры). Мера объединения конечного числа попарно непересекающихся измеримых множеств равна сумме мер этих множеств.

Пусть Xi — измеримые множества (i = 1, 2, ..., m) и

Xi ∩ Xj = ,	i = j, i, j = 1, 2, ..., m.	(42.56)
Докажем, что	m
m
μ i=1 Xi = i=1 μXi.		(42.57)

Мы уже имеем неравенство (42.55), даже без предположения о выполнении условия (42.56). Докажем противоположное неравенство.

Если куб ранга k содержится в некотором множестве Xi, а следова-
тельно, в sk(Xi), то он содержится и в объединении							m
							Xi, а следова-
	m						=1
		, поэтому					i
тельно, в sk	i=1 Xi
		m		m		,
		i=1 sk(Xi) sk		i=1 Xi			(42.58)
откуда
		μ m sk(Xi) μsk			m Xi .		(42.59)
		i=1	(42.6)	i=1

Поскольку множества Xi не пересекаются, то не пересекаются и множества sk(Xi) Xi. В силу этого имеет место равенство

						m
					i
	m
	μ sk(Xi) =					μsk(Xi).		(42.60)
	i=1			(42.6)		=1
Из соотношений (42.59) и (42.60) следует, что
	m
						m
	i=1 μsk(Xi) μsk i=1 Xi .							(42.61)
	m
Множества Xi и Xi		измеримы, поэтому существуют конечные
пределы	i=1
						i = 1, 2, ..., m,
	lim μsk(Xi) = μXi,
	k→∞			m	i	m		(42.62)
	lim μs
	k→∞		k	i=1		i=1	i

Перейдя к пределу при k → ∞ в неравенстве (42.61), в силу равенств (42.62) получим,что

m
i		(42.63)
μXi μ	m Xi.

=1	i=1

5 Л. Д. Кудрявцев