А.В.Шатина МО 2012 версия 20.09.2013

где

41

Задачи выпуклого программирования

Постановка задачи:

				f	x min;
				0
f		: R	n	R j 0,1,...,
	j

f1 x 0,..., fm x 0,	x A ,
m - выпуклые функции,		A R	n

(1)

- вы-

пуклое множество.

Определение. Точка x называется допустимой пуклого программирования, если x A и f1 x 0,...,

в

fm

задаче вы-

x 0 . ▲

Задача выпуклого программирования является выпуклой задачей, т.е. множество допустимых элементов является выпуклым.

Теорема Куна-Таккера.

1) Пусть xˆ absmin з . - точка абсолютного минимума в задаче выпуклого программирования. Тогда существует ненулевой вектор множителей Лагранжа 0 , 1,..., m такой, что вы-

полняются условия: а) принцип

m L x, j f j x : j 0

минимума

min L x, x A

для функции Лагранжа

L x,
ˆ	;

б) условия дополняющей нежесткости:

		f		ˆ	1,..., m
	j		j	x 0, j
в) условия неотрицательности:
	j			0, j 0,1,..., m.

;

в) и

в)

2)Если для допустимой точки

0 0, то xˆ absmin з .

3)Если для допустимой точки

и выполнено условие

ˆ	выполнены условия а), б),
x
ˆ	выполнены условия а), б),
x
				A :
Слейтера (т.е.			x

f	j	x 0,

j

1,..., m

), то

xˆ absmin

з

.

■

Теорема Куна-Таккера дает необходимые и достаточные условия абсолютного минимума в задаче выпуклого программирования.

42

Замечание. Если в выпуклой задаче (1) отсутствует ограни-

чение в виде включения	x A, (т.е.	A R	n	), то условие а) теоре-

мы Куна-Таккера равносильно условию стационарности функции

Лагранжа

x

m j j 0

f

j

x

:

0

xˆ

.

Это следует из того, что

функция Лагранжа

mx j f j x j 0

с неотрицательными мно-

жителями Лагранжа является выпуклой функцией. А по аналогу теоремы Ферма для выпуклых функций условие 0 xˆ является необходимым и достаточным условием абсолютного мини-

мума функции Лагранжа в точке			ˆ
			x .
	Задача. Найти расстояние от точки			M 1, 2 , 3	до конуса
K :	2	2
	x1	x2 x3 0 .

Решение. Формализуем поставленную задачу, стве целевой функции квадрат расстояния от точки принадлежащей конусу:

взяв в каче- M до точки,

x	2	x				2	x				2	min;			1	x		2	x
			2		2					3					x			2
1	1						3								1						3
Составим функцию Лагранжа															x
	x L x,						x				x
										2				2						2
						0	1	1				2	2		3				3
						1		2			2	x3 .
								x1	x2

0

.

Выпишем необходимые условия абсолютного минимума:

а) 0 x ,

																		x1						x2
	2		x , x							, x											,							, 1 ,
		0	1	1		2			2		3		3	1		2			2					2		2
																		x1 x2						x1	x2
x
																					если				2	2			0,
																									x1	x2
			,											y , y		, 1 , y2			y2
	2	0			2		, x				3				2									1,
			1					3					1	1		1				2
																									2	2
																					если				x1	x2			0.

43

б) 1	2	2	x3 0;
	x1	x2			0 .
в) 0 0, 1			2	2
			0 0	1
Если	0 0,		то из	условия а) получим		1 0	, т.е. вектор

множителей Лагранжа равен нулю, поэтому этот случай не подходит.

	Положим		0	1 2 .									Разберем															отдельно два случая:
x2	x2 0 и	x2	x	2	0 .
1	2	1	2
	I.
					x		2		x				2			0,
													2
						1														x
																												0,
					x																	1		1
						1					1								x		2		x			2
																				1						2
												2									x							0,
					x2															x		1			2
																						2		x			2
																					1						2
					x							3											0,
						3												1			x 0,
										x		2			x				2
																			2
						1					1													,	3
					x								x			2	x					2
						3									1							2
					0.
						1
	Рассмотрим два варианта выполнения условия дополняю-
щей нежесткости.
	Iа)
									1 0,
									x				,
										1							1
														2 ,
									x2
									x		3							3		,
																					2						2	,
											3									1						2
											2								2			0.
									1						2
	Следовательно, если										3										2						2	0 , то
																				1						2

xˆ 1, 2 , 3 absmin з, Smin 0 .

														44
Iб)
		1		0,
x			1										1						,
										2					2
	1							x				x						1
															2
									1
											1
					1													2		,
x2											2		x			2
								x
																2
										1
	x	3					3					1		,
							x2			x2						0.
x		3
								1						2

																											1
	1			0,
																											x
																				,								1
	x			1						3						1
		1				3 2 1
								2				3					1
	x2																				,						x2
								3 2 1
	x		3				3							1	0,
																											x		3
					1								2						2
																			2					3	.
			1			2						1
																											1
Следовательно, если																									2			2
																									1	2

0,
															2						2
		1				3								1							2						,
					2				2			2
										1								2
																2						2
				2			3								1							2							,
					2						2		2
										1								2
	1
								2						2													0,
	2						1							2							3
	1
								2						2
																							.
	2						1							2							3
3										2						2
								1 2 , то

ˆ
x
S	min

	1
2
1
1
2		3



2 2

,

2 1

	2
	2 2
	1	2
	2	2
		.
	2

			1	3		2	2	,
,
	, где		2			1	2

	Тогда расстояние от точки M						до конуса
	M , K				1
										2	2
		S	min
				2						1	2

K

равно

3 .

45

II.

IIа)

если 1 2

IIб)

если 3

0, 3

2
1

x		2				x			2				0,
	1								2
														y				0,
												1
					1											1
						2							1			y	2		0,
					3 1 0,
x3
			2			y					2		1,
		1								2
	y
	x				0,
		3
				x								0,
		1							3
					0.
		1
					0,
		1
												0,
								2
	1
						3						0.
x3
0 , то											ˆ		0;0; 3 , Smin 0.
										x
							0,
					1
	x3						0,
																	,
					1											3
																1 ,
	y1 1
	y																			,
					2								2						1
	x				2		x2									0,
				1								2			2		2 3				2
																						1,
	1 3
2							ˆ		0;0;0 , Smin														2	.
2 , то x

Ответ: Если 3 xˆ 1,

	2	2	, то
	1	2

2 , 3 absmin з, M , K 0.

Если	2	2	3	2	2
	1	2		1	2

			1					2
ˆ
x		2		2	,		2		2		,		absmin
		1		2			1		2

, то

з, где 12 3 12 22 ,

46

		M , K			1		2	2	3 .
						2	1	2
							0;0;0 absmin з ,
		2	2			ˆ
	Если 3	1	2 , то
						x
		M , K					2	2	2
							1 2 3 .

Задачи для самостоятельного решения

●

В задачах 4.1-4.5 выяснить, является ли выпуклой заданная функция одной переменной. В случае положительного ответа найти субдифференциал функции.

2

2

x1

x2

x .

4.1. f x min x1

x2

4.2. f x

x 2

2

x

.

4.3. f x max x

2

; x 2 .

4.4. f x

x 1 .

4.5. f x max x , x 1 .

В задачах 4.6-4.8 найти субдифференциалы заданных выпуклых функций.

4.6.

f x

x1 x2

x1

x2

,

4.7.

f x

a, x b

, x R

n

,

4.8.

f x

x1 a1

x2

a2

,

Решить выпуклые задачи:

x R	2		.
a R		n		,

x R2 .

b

R

.

2	2	3 x1 x2 2	min .
4.9. x1	x1x2 x2

4.10.x12 x1x2 4x22 max 2x1, x2 min .

4.11.x12 x22 x1 1 2 x2 2 2 min .

4.12.	x2	x2	2	x	a 2	x	2	a	2	2	min , где
	1	2		1	1

заданные числа.

a	, a	2
1

-

4.13. 2x2	x x	2	x2	2x	x	2	min; x	x	2	1, x	2	x	2.
1	1		2	1			1					1

47

4.14.

x	x	2	4	min,	x2	x2
1					1	2

1

.

4.15. x12 x1x2 4.16. max 2x1,

4x22 2x32 min;

x	2	x2	min,	x2
		1		1

x1 x2

	2x	2
		2

x3 1, x3 2 .

4 .

Занятие 5. Графический метод решения задач линейного программирования

Постановка задачи. Общая постановка задачи линейного программирования состоит в нахождении экстремума линейной

функции

f x	f x				n
		,..., x	n			c	j	x	j
	1
					j 1

при наличии ограничений,

задаваемых в виде линейных уравнений и неравенств:

f x c

x

c

n

x

n

extr

1

1

n

b ,

i 1,...,l,

a

x

j

ij

i

j 1

n

a

ij

x

j

b

,

i l 1,..., m,

i

j 1

x

j

0,

j 1,..., n.

(1)

(2)

(3)

Отметим, что в условии задачи линейного программирования могут содержаться неравенства и противоположного, чем в

(2) знака, однако, такие неравенства легко сводятся к виду (2) умножением на –1.

Если задача линейного программирования содержит только две переменные, и в ее условии нет ограничений в виде равенств (1), то такую задачу можно решить графически.

Рассмотрим задачу:

f x c1x1 c2 x2 extr

a	x	a		x	2	b	, i 1,..., m,
i1	1	i2				i
		x1	0, x2				0 .

(4)

(5)

(6)

На плоскости Ox1x2 любое из неравенств (5) определяет полуплоскость, лежащую по одну из сторон прямой ai1x1 ai2 x2 bi .

48

Для того чтобы определить расположение этой полуплоскости относительно граничной прямой, можно подставить координаты какой-либо точки в соответствующее неравенство (5) и проверить его выполнение. Таким образом, допустимое множество Dз зада-

чи линейного программирования (4)–(6) является пересечением первой четверти, задаваемой неравенствами (6), и полуплоско-

стей, задаваемых неравенствами (5). Поэтому множество

Dз

представляет собой одно из множеств на плоскости Ox1x2 :

а) пустое множество (тогда задача (4)–(6) не имеет реше-

ния);

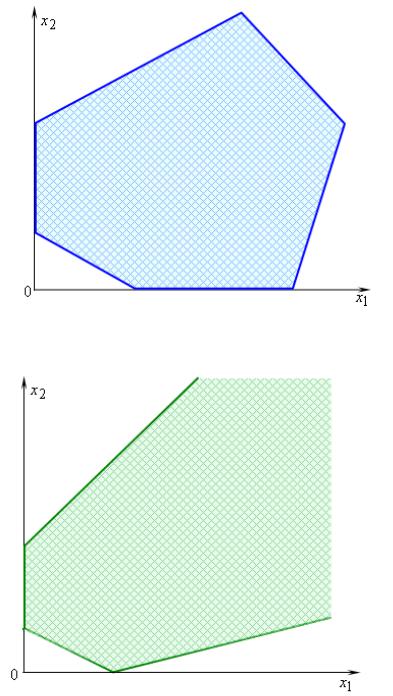
б) выпуклый многоугольник (рис. 5.1); в) неограниченное многоугольное множество (рис. 5.2); г) луч; д) отрезок;

е) точку (тогда эта точка и будет решением задачи).

Для решения задачи линейного программирования в случае,

когда	Dз , рассмотрим множество линий уровня функции
f x :

c x		c	2	x	2	c,
1	1

c

const

.

(7)

Прямые (7) представляют собой семейство параллельных

прямых. Вектор–градиент	f		, c2	e	перпендикулярен
		x c1
прямым (7) и указывает направление возрастания функции						f x .

Если перемешать параллельно самой себе произвольную прямую (7), проходящую через допустимое множество Dз , в направлении

e до тех пор, пока эта прямая будет иметь хотя бы одну общую
точку с множеством Dз , то в своем крайнем положении указан-
ная прямая пройдет через точку множества	Dз , в которой функ-
ция f x принимает максимальное на Dз	значение. Если пере-

мещать произвольную прямую (6) в противоположном направлении до тех пор, пока эта прямая будет иметь хотя бы одну общую точку с множеством Dз , то получим точку, в которой f x при-

нимает минимальное значение на множестве Dз .

49

Рис. 5.1

Рис. 5.2

Заметим, что в случае, когда Dз представляет собой неогра-

ниченное	множество	на плоскости	Ox1x2 , возможно, что
fmax	fmin .	Если прямая (7) параллельна одной из

сторон многоугольника Dз , то решением задачи может быть целый отрезок или даже луч.

50

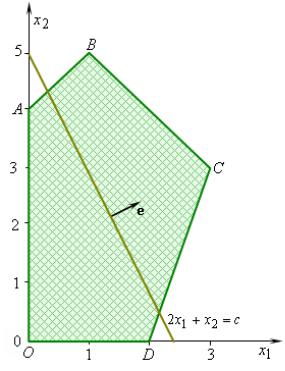
Пример 1. Решить задачу линейного программирования:

2x	x	max
1	2

x		x			2				4;
1
x	x		2				6;
1
3x		x		2				6;
1
x 0,			x			2			0 .
1

Решение. Изобразим на плоскости Ox1x2 допустимое множество

Dз	данной задачи. Оно представляет собой многоугольник
OABCD с вершинами в точках O 0;0 , A 0;4 , B 1;5 , C 3;3 , D 2;0
(рис.	5.3). Построим одну из линий уровня целевой функции
f x	2x1 x2 c . Вектор-градиент e 2;1 указывает направле-
ние возрастания функции f x . Совершая параллельный перенос

линии уровня вдоль направления

e , находим ее крайнее положе-

ние.	В своем крайнем положении прямая			2x1 x2	c	проходит
через	точку C 3;3	многоугольника	Dз .	Откуда	следует, что
3;3 absmax з, fmax		f 3;3 9 .				●

Рис. 5.3