ЦОС №2

8

Кузьмин М.А. гр.110

В-5

(1)

1.Оцените область устойчивости РЦФ2П в зависимости от значений коэффициентов b₁ и b₂ и разбейте ее на под-области для апериодических и колебательных систем. Область устойчивости оценить по характеристическому уравнению.

Устойчивость фильтра определяется значениями коэффициентов b₁ и b₂.

Характеристическое уравнение:

, (1.1)

корни характеристического уравнения (1.1)

, . (1.2)

Фильтр устойчив, если корни характеристического уравнения находятся внутри единичной окружности:

, т.е. (1.3).

а) Если корни вещественные, то в системе устанавливается апериодический режим

б) Если есть комплексно-сопряжённые корни, то система колебательная.

Исходя из вышесказанного, получим следующие выражения:

1. – действительные корни;

2. – комплексно-сопряженные корни;

3. – граница колебательности.

Рассмотрим два случая:

а) Когда , отсюда следует

(1.4)

Решая неравенство (1.4) получим четыре попарно равных неравенства

б) Когда

(1.5)

Исходя из выражений (1.4) и (1.5) получим три условия, на основе которых построим треугольник устойчивости:

– 1-е условие (1.6)

– 2-е условие (1.7)

– 3-е условие (1.8)

Рисунок 1.1 – Треугольник устойчивости

Если точка с координатами (b₁,b₂) внутри треугольника устойчивости, то ЦФ является устойчивым.

Колебательные системы (КС): .

Апериодические системы (АС): .

– граница между апериодическими и колебательными режимами.

1) ;

2) ;

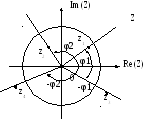
– два полюса на действительной оси Z. То есть область апериодических решений отображается в пары точек на действительной оси Z.

.

Модули – модуль определяется только значением b₂;

при мы подходим к границе устойчивости;

при модуль .

Граница ; отображается на единичную окружность (конкретная точка зависит от коэффициента b₁).

Граница устойчивости:

Два полюса сливаются в один .

2. Определите дисперсию шума АЦП на выходе цифрового фильтра (получите расчетную формулу ). Расчет дисперсии шума АЦП на выходе цифрового фильтра будем производить по формуле

(2.1)

Контурный интеграл находится как сумма вычетов в особых точках подынтегрального выражения, лежащих внутри единичной окружности |z_i| < 1, т.е. полюса H_k(z ^–1) не учитываются, т.к. они лежат вне единичной окружности. Для учета шума квантования АЦП рассмотрим функцию .

– характеристическое уравнение. Z_1,2 – корни уравнения.

;

(2.2)

Полюсы H(z): .

Полюсы H(z ^–1): .

Исходя из сказанного выше, определим среднеквадратическое значение шума АЦП

Подставим z₃ и z₄

После приведения подобных и замены z₁+z₂=b₁ z₁z₂=b_2, получим

(2.3)

3. Нарисуйте структурную схему цифрового фильтра при канонической форме реализации, и последующие пункты задания выполняйте используя эту форму реализации.

Рисунок 3.1 – Структурная схема фильтра для канонической формы реализации

4. Определите выходные дисперсии шумов округления, вносимых при умножении на коэффициенты фильтра b1 и b2.

Рисунок 4.1 – Эквивалентная шумовая схема фильтра для канонической формы реализации

Нахождение среднеквадратического значения шума вносимого при умножении на коэффициент b₁:

.

,

,

.

.

В результате преобразования и подстановки, получаем:

(4.1)

Нахождение среднеквадратического значения шума вносимого при умножении на коэффициент b₂:

.

Вывод аналитического выражения для коэффициента b₂ аналогичен приведенному выше для коэффициента b₁.

(4.2)

5. Определите суммарную дисперсию шумов квантования и округления на выходе цифрового фильтра.

Суммарную дисперсию шумов квантования и округления на выходе цифрового фильтра определим как сумму .

(5.1)

6. При предположении, что один из умножителей на b1 (b2) выполняет операции с сохранением остатка, вычислите выходную дисперсию шумов округления.

При учете остатков шумы дополнительно проходят по цепи вычислителя первой разности (цифрового дифференциатора).

Рисунок 6.1 – Эквивалентная схема умножителя с сохранением остатка

Расчет произведем по следующему выражению

(6.1)

Системная функция фильтра имеет вид (1), тогда функция будет иметь вид

Полюсы H_l(z):

Полюсы H_l(z –1):

Полюс 1/z:

Учитываем только следующие полюсы

Контурный интеграл находится, как сумма вычетов в особых точках подынтегрального выражения получаем сумму трех вычетов:

В результате преобразований и подстановки получаем формулу для расчета дисперсии шума АЦП на выходе цифрового фильтра:

(6.1)

7. Выводы

В ходе выполнения расчетного задания был определен и построен график устойчивости для коэффициентов характеристического уравнения. С помощью графика можно определить области колебательной и системы, и в зависимости от коэффициентов b₁,b₂, можно определить, устойчив фильтр или нет.

На выходе цифрового фильтра дисперсия шума возникает при обработке сигнала, т.к. цифровой фильтр представляет собой вычислительное устройство, в нем выполняются арифметические процессы.

В цифровом фильтре происходит дискретизация сигнала, а потом дискретизированный сигнал квантуется, и при квантовании возникают ошибки округления. Ошибки зависят от разрядности АЦП, чем разрядность выше, тем меньше ошибка.

В цифровом фильтре формирование ошибки зависит от арифметических операций: округления и усечения сигнала. А разница между исходным и округленным значением будет шумом квантования.

При вероятностной оценки ошибки квантования и округления, операции квантования и округления линеаризуем, введя сумматор и источник шума. При этом возникают шумы квантования и округления с дисперсией.