Лабораторная работа №6 измерение ускорения свободного падения с помощью оборотного маятника

Цель работы:

1.Ознакомиться с теорией механических гармонических колебаний.

2.Измерить ускорение свободного падения тел с помощью оборотного маятника.

ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ РАБОТЫ

Процессы, обладающие той или иной степенью повторяемости во времени, называются колебаниями. Описывающие их функции времени обладают свойством периодичности. В частности, для механических колебаний таким свойством обладают обобщенные координаты системы, т.е. величины, однозначно определяющие в каждый момент времени положение системы в пространстве, но не обязательно являющиеся декартовыми координатами.

Различают свободные и вынужденные колебания. Свободными называются колебания, которые совершает система, предоставленная самой себе после какого-либо внешнего воздействия. Вынужденными называются колебания, происходящие под действием внешней периодически изменяющейся силы.

Простейшими колебаниями являются гармонические колебания, при которых обобщенные координаты системы изменяются по закону синуса или косинуса. Этот вид колебаний особенно важен, во-первых, потому, что реальные колебания часто имеют характер, близкий к гармоническим, а, во-вторых, периодические процессы с другой зависимостью от времени могут быть представлены в виде суперпозиции гармонических колебаний.

Гармонические колебания

В качестве примера рассмотрим движение материальной точки (частицы) массой m под действием упругой силы , где , - радиус-вектор частицы относительно положения равновесия.

Уравнение движения частицы в соответствии со вторым законом Ньютона запишется в виде

,

или

. (6.1)

Поскольку момент упругой силы относительно точки , то момент импульса частицы относительно той же точки . Поэтому движение будет происходить в фиксированной плоскости, перпендикулярной вектору . Введем в этой плоскости систему координат ХОУ с началом в положении равновесия частицы. Тогда, проектируя уравнение (1) на координатные оси, приходим к системе двух независимых дифференциальных уравнений

, (6.2)

. (6.3)

Будем искать решение уравнения (2) в виде

, (6.4)

где , , - некоторые константы. Дважды дифференцируя функцию (6.3) по времени, находим

. (6.5)

Подставляя (6.5) и (6.4) в (6.2), получаем

.

Поскольку не является тождественным нулем, то функция (6.4) будет решением уравнения (6.2) при произвольных и , но с

. (6.6)

Движение частицы, описываемое законом (6.4), называют гармоническими колебаниями.

Постоянную (6.6), определяющую период функции (6.4) (время одного полного колебания), называют циклической, или круговой частотой колебаний. Интервал времени называют периодом колебаний. Функцию называют фазой колебаний. Константу называют амплитудой колебаний. Значения постоянных и определяется из начальных условий и , задающих соответственно начальное положение и начальную скорость частицы.

Совершенно аналогично решение уравнения (6.3) запишется в виде

. (6.7)

Функции (6.4) и (6.7) определяют кинематический закон движения частицы под действием упругой силы. Вид траектории движения в плоскости ХОУ зависит от начальных условий, а следовательно, от значений констант .

В частности, если и , то уравнение траектории имеет вид , и частица совершает гармонические колебания с частотой и амплитудой вдоль диагонали прямоугольника со сторонами 2А и 2В (рис.6.1). Если же , а , то уравнение траектории имеет вид

,

т.е. частица движется по эллипсу с полуосями А и В (рис.6.2)

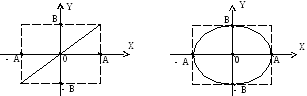
Рис. 6.1 Рис. 6.2

Таким образом, в данном случае периодическое движение по замкнутой кривой может рассматриваться как суперпозиция двух гармонических взаимно перпендикулярных колебаний.