Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Петрозаводский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ОСНОВЫ МАТЕМАТИЧЕСКОЙ ФИЗИКИ.doc

Скачиваний:

163

Добавлен:

14.05.2015

Размер:

2.35 Mб

Скачать

☆

1 / 101 2 3 4 5 6 7 8 9 10 > Следующая >>>

Министерство образования и науки Российской федерации

Петрозаводский государственный университет

Кольский филиал

«ОСНОВЫ МАТЕМАТИЧЕСКОЙ ФИЗИКИ»

Учебно-методическое пособие

Апатиты

2004

УДК 517.946

ОСНОВЫ МАТЕМАТИЧЕСКОЙ ФИЗИКИ. /Учебно-методическое пособие. //составители - Терещенко С.В., Андреев М.Ю./ –Апатиты.: Издание КФ ПетрГУ. -2004. –70 с.

Пособие охватывает следующие разделы дисциплины: приведение уравнений к каноническому виду и использование характеристик для нахождения общего решения; решение начальных и граничных задач уравнений гиперболического, параболического и эллиптического типов.

В каждом параграфе приводятся необходимые теоретические сведения. Типовые задачи даются с подробными решениями. В пособии имеются задания для самостоятельной работы студентов. Варианты контрольных работ, содержащиеся в пособии, могут быть использованы как для работы со студентами очного, так и заочного отделения.

Рецензенты:

кафедра высшей математики филиала Санкт-Петербургского инженерно-экономического университета в г. Апатиты, заведующий кафедрой высшей математики филиала, доктор физико-математических наук Мингалев В.С.;

кафедра информационных систем Кольского филиала Петрозаводского государственного университета, доктор технических наук Богатиков В.Н.

Печатается по решению редакционно-издательского совета Петрозаводского государственного университета в качестве учебно-методического пособия

Государственного университета

Кольский филиал, 2004

Внимание!!! контрольная работа должна быть выполнена в рукописном виде. Иначе она принята не будет. Варианты с 6 по 10.

СОДЕРЖАНИЕ

1. ТИПЫ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА В ЧАСТНЫХ ПРОИЗВОДНЫХ. ПРИВЕДЕНИЕ К КАНОНИЧЕСКОМУ ВИДУ 4

Задания для самостоятельной работы 11

2. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА 11

2.1. Уравнение колебаний струны 11

2.2. Формула Даламбера 13

Задания для самостоятельной работы 16

2.3. Решение волнового уравнения методом Тейлора 16

Задания для самостоятельной работы 18

2.4. Краевые задачи для уравнений гиперболического типа 18

2.5. Решение краевой задачи методом Фурье 22

Задания для самостоятельной работы 28

3. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА 29

3.1. Уравнение теплопроводности и постановка краевых задач 29

3.2. Решение краевых задач методом Фурье 32

3.3. Неоднородное уравнение теплопроводности 37

Задания для самостоятельной работы 40

3.4. Задача Коши для уравнения теплопроводности 40

3.5. Решение уравнения теплопроводности методом Тейлора 42

Задания для самостоятельной работы 44

4. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА 44

4.1.Задачи, приводящие к уравнениям эллиптического типа 44

4.2. Решения краевой задачи для уравнения Лапласа внутри круга и вне его 46

Задания для самостоятельной работы 52

Ответы на задания для самостоятельной работы 53

КОНТРОЛЬНЫЕ РАБОТЫ 55

Решить краевую задачу для уравнения Лапласа в круге 65

2. 65

Решить краевую задачу для уравнения Лапласа в круге 65

Список использованных источников 66

1. Типы уравнений второго порядка в частных производных. Приведение к каноническому виду

Рассмотрим уравнение второго порядка

, (1)

которое можно также записать в виде

где u, a, b, c –функции х и у.

Уравнению (1) можно придать и другой вид, если произвести замену независимых переменных

с якобианом преобразования

допускающим обратное преобразование. Тогда, вычислив в новых переменных производные

(2)

приведем уравнение (1) к виду

(3)

где

Если функции выбрать таким образом, чтобы в новых переменных часть коэффициентов обратилась в нуль, а уравнение (3) приняло наиболее простой вид, то такой вид уравнения (3) называютканонической формой исходного уравнения (1).

Переход к канонической форме можно осуществить с помощью общих интегралов обыкновенного дифференциального уравнения второй степени

, (4)

которое называется характеристическим для уравнения (1), а его интегралы характеристическими кривыми, или характеристиками.

Если - общий интеграл характеристического уравнения (4), то полный дифференциал этой функции равен

следовательно, вдоль характеристической кривой имеем

отсюда

(5)

подставляя (5) в (4), получим

или после сокращения на (dx)², получим

. (6)

Таким образом, функция является решением дифференциального уравнения первого порядка второй степени (6).

Рассмотрим характеристическое уравнение (4). Разрешим это уравнение относительно производной

которое распадается на два уравнения

. (7)

Знак подкоренного выражения в уравнениях (7) определяет тип уравнения (1).

I. Если D > 0, то уравнение (1) является уравнением гиперболического типа и характеристическое уравнение распадается на два уравнения (7). Следовательно, оно имеет два интеграла, т.е. два семейства характеристик:

Тогда с помощью преобразования независимых переменных

, (8)

можно перейти к уравнению (3), в котором с учетом уравнения (6) коэффициенты А и С равны нулю, т.е.

(9)

которое можно привести к виду

(10)

являющемуся канонической формой уравнений гиперболического типа.

II. Если D = 0, то уравнение (1) является уравнением параболического типа и уравнения характеристик (7) принимает вид одного уравнения

которое имеет только одно семейство характеристик:

В этом случае нужно произвести замену переменных

, (11)

где - какая-нибудь произвольная функция, линейно независимая с функцией, и для которой.

После такой замены в уравнении (3) коэффициент А =0, но так как для уравнений гиперболического типа , то, следовательно, иВ =0. Поэтому уравнение (1) приводится к канонической форме вида

. (12)

III. Если D < 0, то уравнение (1) является уравнением эллиптического типа и характеристическое уравнение приводит к двум уравнениям в комплексной форме:

, (13)

следовательно, уравнения (13) имеют два комплексно-сопряженных интеграла

, (14)

причем функции являются действительными функциями своих аргументов, аявляются решениями уравнения (6) в комплексной области

После преобразования переменных приходим к тому, что в уравнении (3) коэффициент В = 0, коэффициенты А и С равны между собой: А = С. Поэтому после преобразования уравнение (3), являющееся канонической формой уравнения (1), принимает вид

. (15)

Пример 1. Привести к каноническому виду уравнение:

. (1.1)

▲Запишем общий вид уравнения второго порядка

(1.2)

и сравним коэффициенты при производных в уравнении (1.2) и в исходном (1.1):

Определим, к какому типу принадлежит исходное уравнение:

следовательно, исходное уравнение (1.1) принадлежит к уравнениям гиперболического типа.

Осуществим переход к канонической форме с помощью общих интегралов характеристического уравнения (4). В нашем случае это уравнение имеет вид:

Следовательно, С₁ и С₂ определяют уравнения семейств характеристик. Тогда преобразование независимых переменных (8) будет иметь вид

Найдем в новых переменных

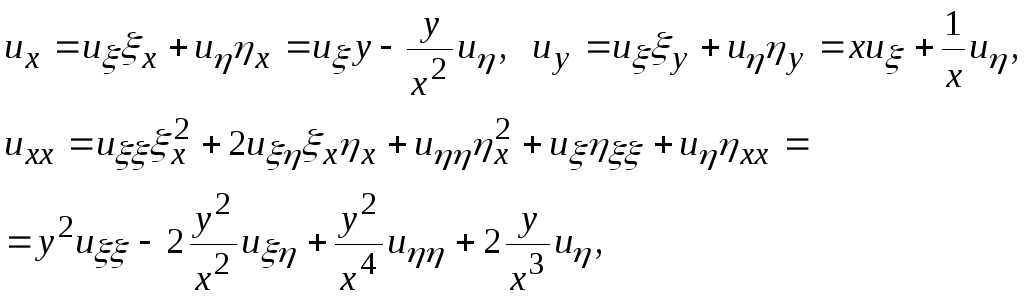
.Таким образом, исходное уравнение (1.1) в новых переменных имеет вид:

и после преобразований, получим

с учетом того, что каноническая форма исходного уравнения имеет вид:

.▲

Пример 2. Привести к каноническому виду уравнение:

. (2.1)

▲ Запишем общий вид уравнения второго порядка

(2.2)

и сравним коэффициенты при производных в уравнении (2.2) и в исходном (2.1):

Определим, к какому типу принадлежит исходное уравнение (2.1)

следовательно, исходное уравнение (2.1) принадлежит к уравнениям параболического типа.

Произведем замену . Вычислим:

Подставим полученные производные в исходное уравнение (2.1) и после преобразований, получим

так как .

Таким образом, окончательно каноническая форма исходного уравнения (2.1) имеет вид:

.▲

Пример 3. Привести к каноническому виду уравнение:

▲ Запишем общий вид уравнения второго порядка

и сравним коэффициенты при производных в уравнении и в исходном:

Определим, к какому типу принадлежит исходное уравнение

следовательно, исходное уравнение принадлежит к уравнениям эллиптического типа.

Следовательно, получаем два семейства мнимых характеристик

Произведем замену и вычислим:

Подставим полученные производные в исходное уравнение и после преобразований окончательно получим каноническую форму исходного уравнения

.▲

Приведение исходного уравнения к канонической форме в ряде случаев позволяет достаточно легко найти решение исходного уравнения. Поскольку в данном методе используется характеристическое уравнение (4), то данным метод нахождения решения называется методом характеристик. Рассмотрим примеры нахождения решения уравнений методом характеристик.

Пример 4. Найти общее решение уравнения:

▲ Запишем общий вид уравнения второго порядка

и сравним коэффициенты при производных в этом уравнении и в исходном:

Найдем в новых переменных

Подставим полученные производные в исходное уравнение, и после преобразований окончательно получим каноническую форму исходного уравнения

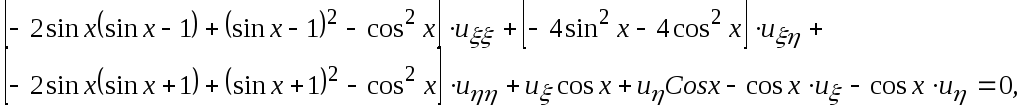
или

Интегрируя дважды это уравнение, получим решение

Возвращаясь к «старым» переменным х и у, запишем окончательно общее решение исходного уравнения

.▲

Пример 5. Найти решение уравнения

▲ Во-первых, осуществим переход к канонической форме с помощью общих интегралов характеристического уравнения (4). В нашем случае это уравнение имеет вид: