Рис. 7.7

Рис. 7.8

Рис. 7.9

Рис. 7.10

Разность между возможным для данного порядка кривой количеством двойных точек и существующим называется жанром кривой. Число возможных двойных точек (узловых, изолированных и возврата) определяется формулой

d = (n −1)(n −2) , 2

где n – порядок кривой.

На рис. 7.2 изображена кривая нулевого жанра. Кривые нулевого жанра называют рациональными. Такие кривые получили широкое распространение в конструировании гладких обводов.

7.4. Пространственные кривые

На чертеже пространственная кривая задается своими ортогональными проекциями. Свойства пространственной кривой можно исследовать по ее проекциям. Для проекций пространственных и плоских кривых справедливы следующие утверждения:

- касательная к кривой проецируется в касательную к ее проекции, если направление проецирования не параллельно касательной;

- в общем случае порядок кривой и ее проекции равны.

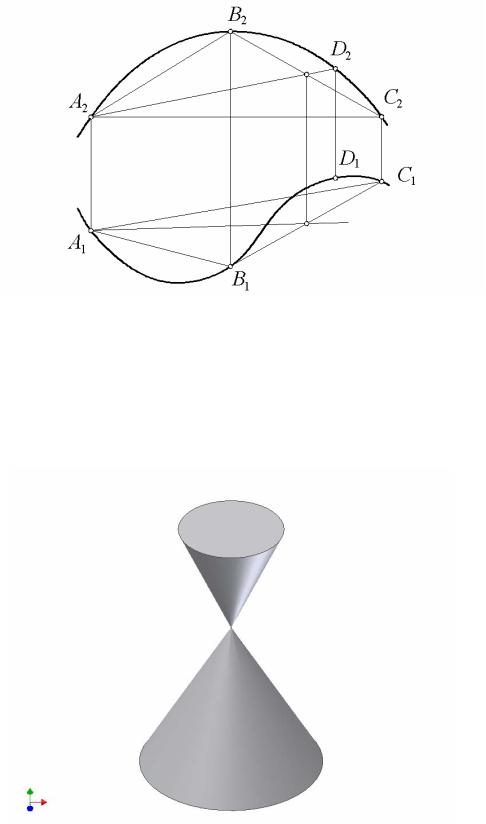
Для того, чтобы по чертежу кривой выяснить, какая кривая задана – плоская или пространственная, нужно, на кривой выбрать три произвольные точки A,B,C и проверить, расположена ли произвольная точка D в плоскости Γ(A, B,C) . Кривая, изображенная на рис. 7.11, является

пространственной, так как точка D не принадлежит плоскости Σ(A,B,C) .

Рис. 7.11

7.5. Конические сечения

Коническими сечениями называют кривые второго порядка, которые получаются в результате пересечения поверхности прямого кругового конуса (рис. 7.12) различными плоскостями.

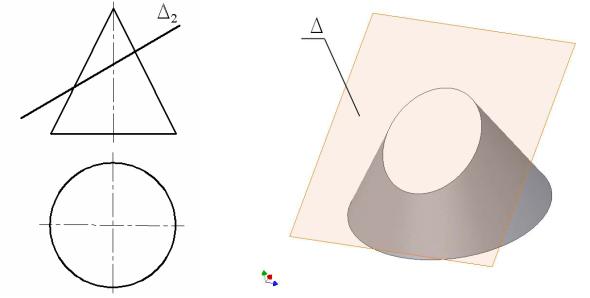
Рис. 7.22

Если секущая плоскость (рис. 7.13, 7.14) пересекает все образующие конуса, то в сечении получаем эллипс. Эллипс содержит пару сопряженных взаимно перпендикулярных диаметров, называемых большой и малой осями.

Рассмотрим построение эллипса по заданным большой a и малой b осям. Вычерчиваем взаимно перпендикулярные прямолинейные отрезки a и b, пересекающиеся между собой в средних точках (рис. 7.15a). Концы отрезков a и b будут совпадать с вершинами эллипса (рис. 7.6). Точка O пересечения осей a и b является центром эллипса.

Рис. 7.13

Рис. 7.14

Строим две окружности, центры которых совпадают с точкой O – центром эллипса (рис. 7.15 б). Диаметры окружностей равны длинам соответствующих осей эллипса. Из центра эллипса O проводим любую прямую OJ '. Из точки J пересечения данной прямой с окружностью меньшего диаметра проводим прямую, перпендикулярную малой оси b эллипса, а из точки J ' – прямую, перпендикулярную большой оси a эллипса. Точка F пересечения этих двух прямых принадлежит эллипсу. Повторяем эту графическую операцию необходимое число раз. В результате получим точки, соединяя которые с помощью лекала, получим эллипс k (рис. 7.15 в).

На рис. 7.16, 7.17 показано коническое сечение, полученное как результат пересечения поверхности конуса плоскостью Σ, параллельной одной из образующих конуса. Такое сечение является параболой.

Если секущую плоскость Γ провести параллельно двум образующим поверхности конуса, то в сечении получим гиперболу (рис. 7.18, 7.19).

Если секущая плоскость Φ перпендикулярна оси конуса, то сечением будет окружность (рис. 7.20, 7.21).

Если секущая плоскость Т проходит через вершину конуса, то в сечении получается коника, распавшаяся на две прямые – образующие конуса (рис.7.22, 7.23).

а)

б)

в)

Рис. 7.15

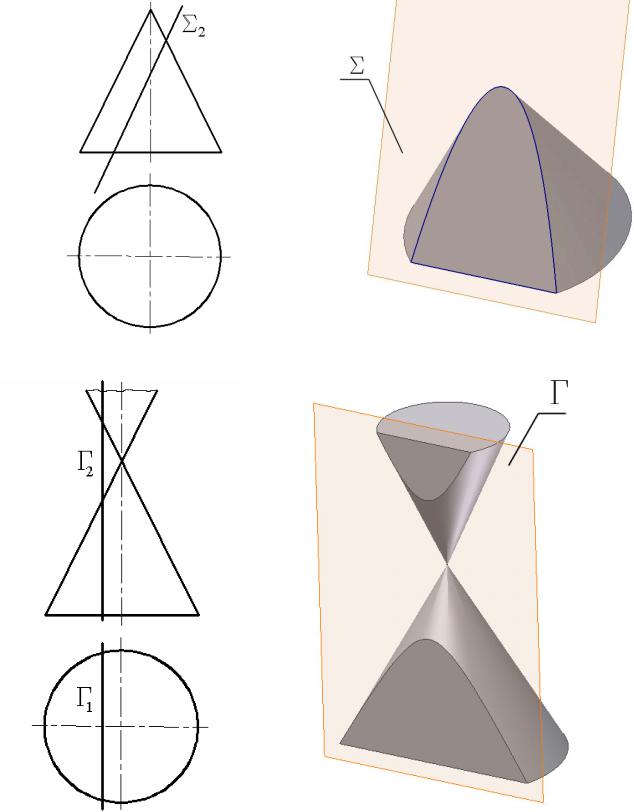
Рис. 7.16

Рис. 7.17

Рис. 7.18

Рис. 7.19