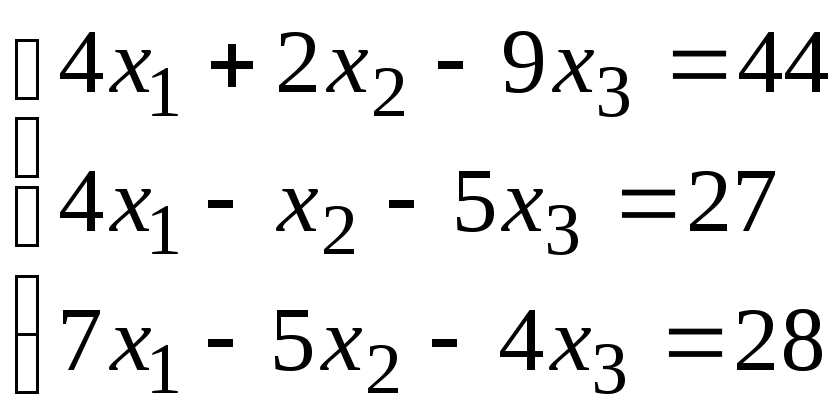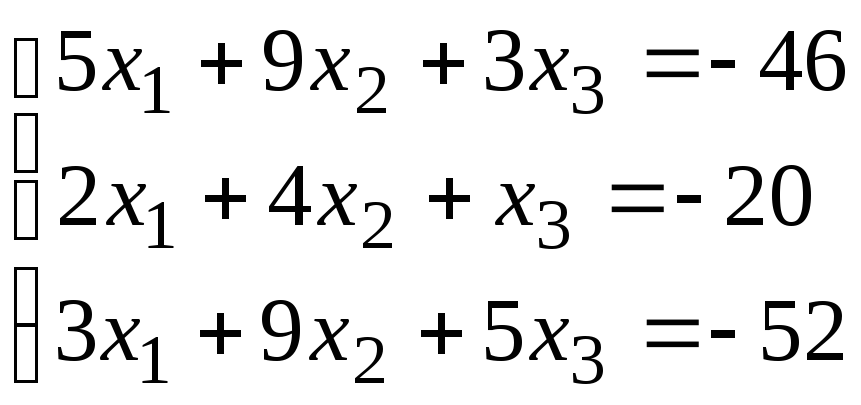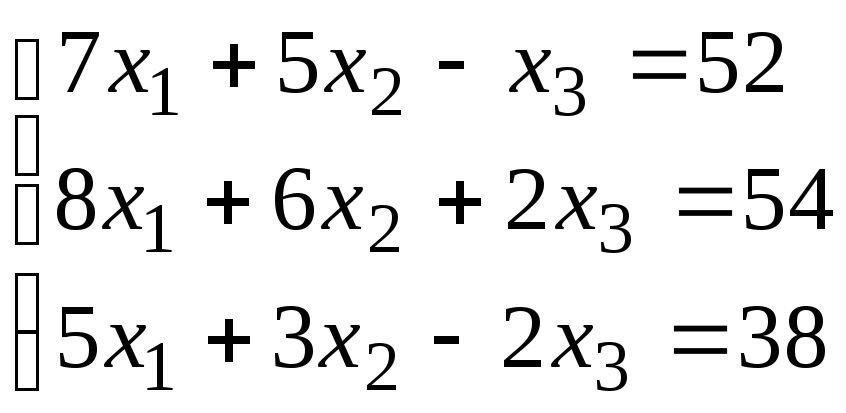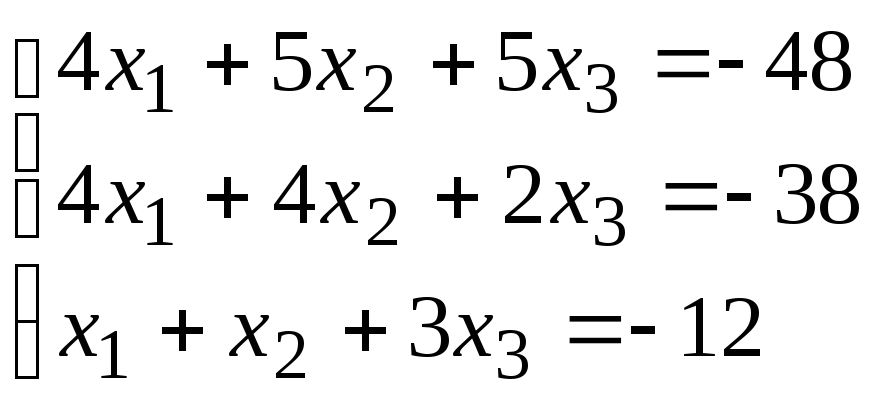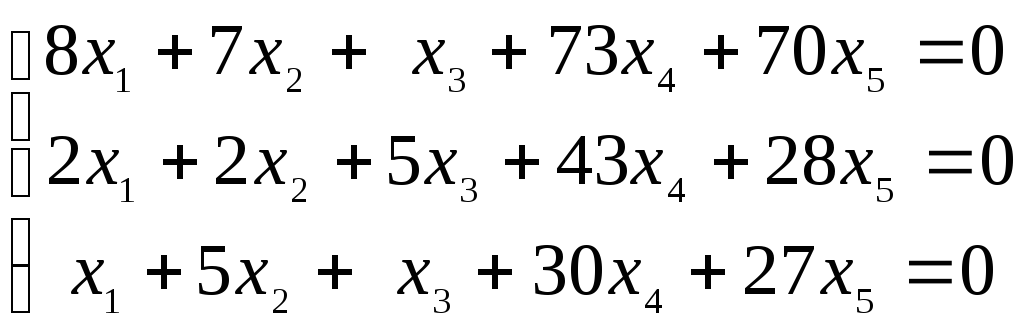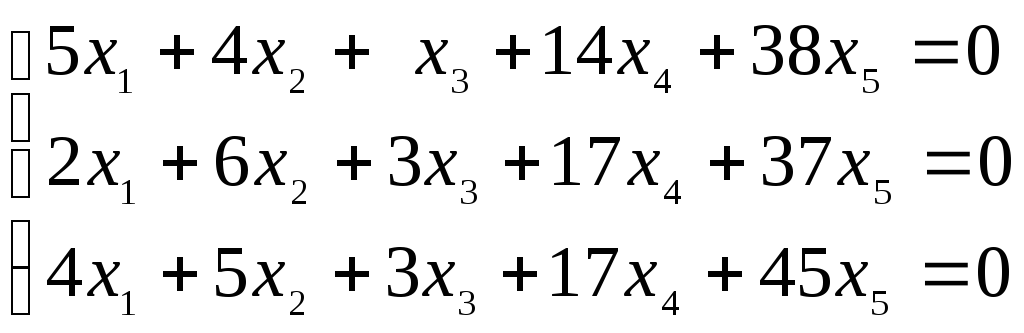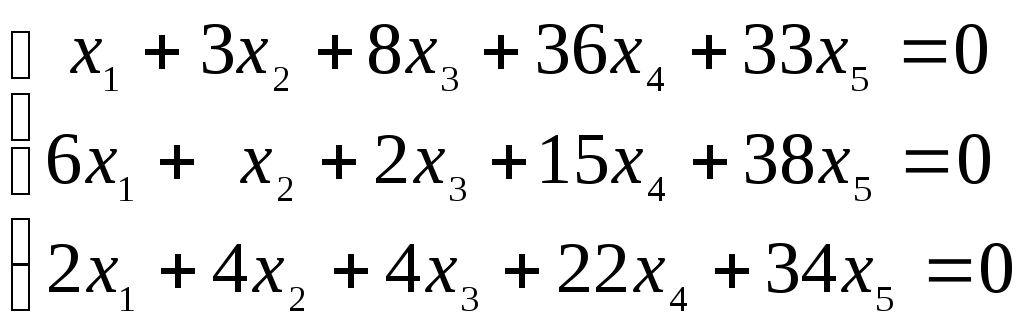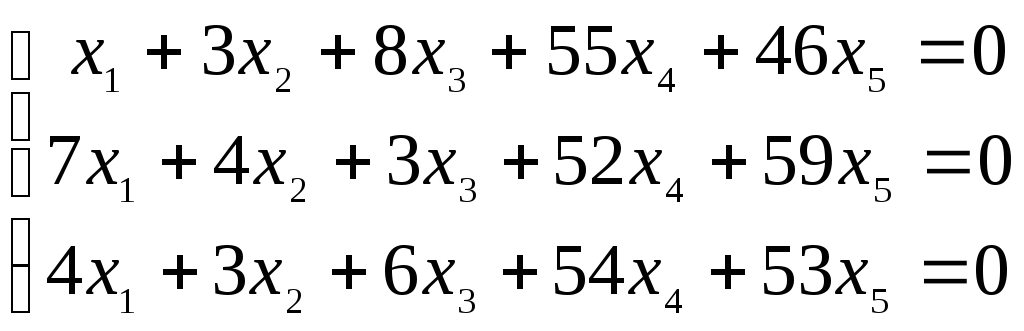- •Министерство образования и науки Российской Федерации
- •Алгебра и геометрия
- •090900 – «Информационная безопасность» и 090303 – «Информационная безопасность автоматизированных систем»
- •1. Матрицы и определители
- •2. Невырожденные системы линейных алгебраических уравнений
- •3. Однородные системы линейных алгебраических уравнений
- •4. Операции над векторами в произвольном базисе
- •5. Операции над векторами в ортонормированном базисе
- •6. Собственные значения и собственные векторы линейного оператора
- •7. Прямая линия на плоскости
- •8. Преобразование уравнения линии второго порядка к каноническому виду
- •9. Прямая линия в пространстве и плоскость
2. Невырожденные системы линейных алгебраических уравнений
Постановка задачи
Решить невырожденную систему трех линейных алгебраических уравнений с тремя неизвестными матричным методом, по правилу Крамера и методом Гаусса.
План решения
Записываем матрицу
системы A
и вычисляем ее определитель detA.
Убеждаемся, что он не равен нулю.
Следовательно, система уравнений имеет
единственное решение. Находим обратную
матрицу
![]() .
Умножая слева обе части матричного
равенстваАХ = В
на А–1,
получаем решение системы – матрицу-столбец
Х = А–1В.
.
Умножая слева обе части матричного
равенстваАХ = В
на А–1,
получаем решение системы – матрицу-столбец
Х = А–1В.
Вычисляем
определители Δ1 ,
Δ2 ,
Δ3 ,
полученные из определителя Δ = detA
заменой соответственно первого, второго
и третьего столбцов – столбцом свободных
членов. По формулам Крамера:
![]() ,i = 1, 2, 3
находим решение системы уравнений.
,i = 1, 2, 3
находим решение системы уравнений.
Расширенную матрицу системы уравнений элементарными преобразованиями приводим к ступенчатому виду. По ступенчатой матрице восстанавливаем систему уравнений и решаем ее снизу вверх.
Условие задачи
Решить невырожденную систему трех линейных алгебраических уравнений с тремя неизвестными (табл. 2) матричным методом, по правилу Крамера и методом Гаусса.
Таблица 2
|
№ |
Система уравнений |
№ |
Система уравнений |
№ |
Система уравнений |
|
1 |
|
2 |
|
3 |
|
|
4 |
|
5 |
|
6 |
|
|
7 |
|
8 |
|
9 |
|
Окончание табл. 2
|
№ |
Система уравнений |
№ |
Система уравнений |
№ |
Система уравнений |
|
10 |
|
11 |
|
12 |
|
|
13 |
|
14 |
|
15 |
|
|
16 |
|
17 |
|
18 |
|
|
19 |
|
20 |
|
21 |
|
|
22 |
|
23 |
|
24 |
|
|
25 |
|
26 |
|
27 |
|
|
28 |
|
29 |
|
30 |
|
3. Однородные системы линейных алгебраических уравнений
Постановка задачи
Найти нормальную фундаментальную систему решений однородной системы линейных алгебраических уравнений и записать общее решение системы.
План решения
Записываем основную матрицу системы и элементарными преобразованиями преобразуем ее к ступенчатому виду. По ступенчатой матрице восстанавливаем систему уравнений. Получаем трапецеидальную систему r уравнений с n неизвестными. Определяем, какие неизвестные в системе будут основными, какие свободными. Основные неизвестные оставляем слева, свободные переносим в правые части уравнений.
Для нахождения нормальной фундаментальной системы решений l1 , l2 , …, lk последовательно каждой свободной неизвестной присваиваем единичное значение, а остальным свободным неизвестным нулевое значение. Решая полученные системы уравнений, находим l1 , l2 , …, lk .
Записываем общее
решение однородной системы:
![]() ,
гдеc1 ,
c2 ,
…, ck
– произвольные постоянные.
,
гдеc1 ,
c2 ,
…, ck
– произвольные постоянные.
Условие задачи
Найти нормальную фундаментальную систему решений однородной системы линейных алгебраических уравнений (табл. 3) и записать общее решение системы.
Таблица 3
|
№ |
Система уравнений |
№ |
Система уравнений |
|
1 |
|
2 |
|
|
3 |
|
4 |
|
|
5 |
|
6 |
|
|
7 |
|
8 |
|
|
9 |
|
10 |
|
|
11 |
|
12 |
|
Окончание табл. 3
|
№ |
Система уравнений |
№ |
Система уравнений |
|
13 |
|
14 |
|
|
15 |
|
16 |
|
|
17 |
|
18 |
|
|
19 |
|
20 |
|
|
21 |
|
22 |
|
|
23 |
|
24 |
|
|
25 |
|
26 |
|
|
27 |
|
28 |
|
|
29 |
|
30 |
|