Задачи для самостоятельного решения
Задача 1. Найти хроматическое число и хроматический индекс графа.
v4 v2
v5 v3 v1
v7 v6
v2 v3
v9 v7 v1
v4
v8
v6 v5
Задача 3. Правильно выполнить раскраску вершин и ребер графа.
v3 v2 v7 v2
v8
v5 v4 v1 v3 v1
v7 v6 v6 v5 v4
§ 6. Представление графов в памяти компьютера. Код Харари
Пусть дан граф с n вершинами. Пронумеруем вершины произвольно и составим матрицу смежности А. Так как граф неориентированный, то она будет симметрична относительно главной диагонали, поэтому достаточно взять ее верхний треугольник А'.
A'
Расположим А' в виде двоичной строки (слева направо и сверху вниз). Меняя нумерацию вершин, мы получим другие двоичные строки. Сравним их между собой как двоичные числа. Наибольшее из двоичных чисел называется кодом Харари, а возникшую при этом нумерацию вершин – канонической. Код Харари определяет граф однозначно, но не всякое число может быть кодом Харари.
Примеры решения задач
Задача 1. Найти код Харари графа.
Решение. Занумеруем вершины графа, выпишем матрицу смежности и ее верхний треугольник.
1
3 4
2
,
верхний треугольник = 1111 011 0002=98410.
Легко увидеть, что данная нумерация вершин является канонической, так как, сменив нумерацию вершин, получим числа меньше числа 984. Следовательно, кодом Харари данного графа является число 984.
Задача 2. Восстановить и нарисовать граф по числу 698 как по ходу Харари. Проверить, действительно ли нумерация вершин каноническая (т.е. является ли число кодом Харари).
Решение. Переведем число 698 в двоичную форму, для чего будем делить его на 2, записывая справа от черты остатки от деления, а слева на следующей строке частные.
698|0
349|1
174|0
87|1
43|1
21|1
10|0
5|1
2|0
1|
Записываем число, начиная с последнего частного и далее все остатки снизу вверх: 1010111010. Код Харари должен быть треугольным числом, т.е. иметь длину 1,3,6,10,15,21 и т.д., если длина не совпадает ни с одним из этих чисел, то добавляем слева необходимое количество нулей. Для числа 698 этого делать не нужно, так как треугольное число равно 10.
Разбиваем число на разряды: 1010-111-01-0, выписываем эти числа в верхний треугольник матрицы, затем восстанавливаем всю матрицу, записывая ее строки по столбцам:
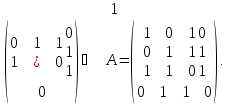
Восстановим
по этой матрице граф с четырьмя вершинами
2 1
3 4
Заметим, что нумерация вершин не является канонической. Перенумеруем вершины.
2 1
3 4
Запишем матрицу смежности для получившегося графа
верхний треугольник = 11100110012=92110. 921>698, значит, число 698 кодом Харари не является.
Задачи для самостоятельного решения
Задача 1. Найти код Харари графа.
Задача 2. Восстановить граф по числу а) 527; б) 784; в) 956 как по коду Харари.
Задача 3. Существует ли граф с кодом Харари 282?
§7. Деревья и ордеревья. Префиксный код бинарного
ордерева. Код Прюфера
Связный граф без циклов называется деревом.
не
дерево
дерево
Орграф называется ордеревом с корнем х0, если:
в вершину х0 не заходит ни одна дуга;
в остальные вершины заходит единственная дуга;
граф не содержит контуров.
Ордерево называют бинарным, если каждая вершина имеет не более двух потомков.
Префиксный код бинарного ордерева
Каждой вершине будем сопоставлять двоичное число (двоичную строку). Корню ничего не сопоставляем, его левому потомку – 0, правому – 1. Потомкам 0 сопоставляем 00 и 01, а потомкам 1-10 и 11 и т.д.
Оказалось, что достаточно хранить двоичные строки не для всех вершин, а только для висячих (не имеющих потомков) {00;010;110}. Это и есть префиксный код бинарного дерева. Он определяет ордерево однозначно.
Код Прюфера
Пусть дано дерево или ордерево с n пронумерованными вершинами. Действуем по алгоритму:
В списке всех вершин 1..2..3..n слева направо ищем первую висячую вершину. Обозначим ее номер а1.
Вершина а1, будучи висячей, смежна с единственной вершиной b1, которую заносим в новый список – будущий код Прюфера, а вершину а1 удаляем и из списка и, из дерева.
Повторяем шаги 1,2 n-2 раза. Заметим, что дерево все время уменьшается и в нем иногда возникают новые висячие вершины.
В итоге получаем новый список {b1,b2,…,bn-1} – код Прюфера. Он определяет дерево однозначно (в ордереве на последнем шаге может возникнуть два варианта).