
Метод. указания к РГР
.pdfТаблица 2
Исходные данные к заданию 2
|
|
Числовые значения параметров по вариантам |
|
|||||||||
Параметр |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
10 |
|
|
|
|
||||||||||
T1, Нм |
100 |
|
120 |
80 |
200 |
400 |
350 |
480 |
120 |
160 |
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
T2, Нм |
250 |
|
220 |
250 |
280 |
490 |
450 |
500 |
80 |
40 |
|
260 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Т3, Нм |
60 |
|
80 |
100 |
220 |
110 |
80 |
220 |
350 |
260 |
|
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
d, мм |
20 |
|
30 |
25 |
35 |
22 |
32 |
24 |
34 |
28 |
|
38 |
|
|
|
|
|
|
|
|
|
|
|
|
|
l, м |
0,2 |
|
0,3 |
0,4 |
0,1 |
0,2 |
0,3 |
0,4 |
0,2 |
0,1 |
|
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Построить эпюру углов поворота (закручивания) сечений
стержня по зависимости i |
(Тi li ) / (Gi I pi ). Модуль сдвига чугуна – |
|
G 4 104 |
МПа, стали – G |
8 104 МПа. |
ч |
ст |
|
ПРИМЕР РАСЧЁТА
К круглому чугунному брусу, закреплённому с одной стороны в
заделке, |
приложены вращающие моменты (рис. 4, а) T1 400 Н·м, |
T2 250 |
Н·м, T3 100 Н·м, длина l 0,2 м, наружный диаметр d 30 |
мм, отношение внутреннего диаметра к наружному d0 / d 0,8. Построить эпюры крутящих моментов, касательных напряжений и углов закручивания. Определить коэффициент запаса прочности бруса при модуле сдвига чугуна Gч 4 104 МПа и продольных касательных напряжениях lim 90 МПа.
Решение
1. Разбиваем брус вдоль продольной оси на четыре силовых участка. Границами участков являются границы бруса и сечения, в которых приложены вращающие моменты. Определение реакций в защемлении не обязательно, так как внутренние силовые факторы – крутящие
11
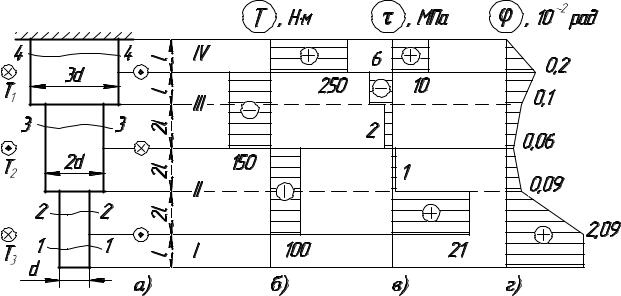
моменты – можно найти методом сечений, перемещаясь вдоль продольной оси от свободного конца стержня (бруса) к защемлению (на рис. 4, а – снизу вверх). Мысленно проведём на первом силовом участке сечение 1-1 и, отбросив верхнюю часть бруса, рассмотрим равновесие нижней части. На первом участке внешние силовые факторы отсутствуют, поэтому внутренний крутящий момент T1 0.
Рис. 4. К расчёту стержня на кручение: а – расчётная схема стержня; б
– эпюра крутящих моментов Т; в – эпюра касательных напряжений ; г – эпюра узлов закручивания сечений
Выполним аналогичные операции на втором участке. К нижней части бруса сечения 2-2 приложим внешний вращающий момент Т3 и внутренний крутящий момент Т2, который условно считаем положительным, если при взгляде на сечение со стороны внешней нормали крутящий момент Т2' направлен против часовой стрелки. Следует всегда задавать Т' положительным (против часовой стрелки), тогда результат всегда будет получаться правильным по знаку (против часовой стрелки – плюс, а по часовой – минус)..
Для второго участка уравнение статического равновесия имеет
вид
M zi Ti 0; |
T3 T2 |
' 0; |
T2 |
' T3 100 Н·м. |
Значение и знак «плюс» показывают, что крутящий момент на первом участке постоянный и направлен против часовой стрелки. На эпюре это прямая, параллельная базисной линии (рис. 4, б). Условие
12
равновесия нижней части бруса на третьем участке имеет вид
Ti 0; T3 T2' T3' 0; T3' T3 T2 100 250 150 Н·м.
Крутящий момент Т3 на всем участке постоянный и направлен по часовой стрелке. Его эпюра представлена прямой, параллельной базисной линии.
Применим метод сечений для четвертого участка. Уравнение статического равновесия имеет вид
Ti 0; T3 T2 T4' T1 0; T4' T3 T2 T1 100 250 400 250 Н·м.
Крутящий момент Т4' на всем четвертом участке постоянный и направлен против часовой стрелки. Его эпюра представлена прямой, параллельной базисной линии (рис. 4, б).
2. Построим эпюру касательных напряжений τ для определения наиболее напряженных сечений бруса.
Предварительно необходимо рассчитать геометрические характеристики сечений круглого стержня (бруса).
Полярный момент сопротивления круглого сечения диаметром d определяют по формуле
|
|
|
Wp I p / max (2 d 4 ) / (64d) d3 / 32 0,2d 3 . |
|
|
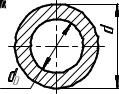
Для круглого полого сечения (рис. 5) с наружным диаметром d, |
|||
внутренним d0 имеем |
|
|||
Wp |
(I p |
I p |
) / max ( d 4 d0 |
4 ) / (32 0,5d) ( d3 (1 (d0 / d)4 ) /16 , |
|
|
0 |
|
|
|
|
|
Wp 0,2d3 (1 (d0 / d)4 ). |
|
|
|
|
В нашем случае для полого бруса переменного се- |
|
|
|
|
чения имеем: |
|
|
|
|
при d1 d 30 мм |
|
|
|
|
Wp 0,2d13 (1 (d0 |
/ d1)4 ) 0,2 303 1 0,84 3,2 103 мм3; |
|
|
|
1 |
|
Рис. 5. Сече- |
|
|
при d2 3d |
3 30 90 мм |
ние полого Wp |
0,2d23 (1 (d0 |
/ d2 )4 ) 0,2 903 1 0,84 86,1 103 ммз; |
||
стержня (ва- |
2 |
|
|
|
|
|
|
||
ла) |
|
|
при d3 2d 2 30 60 мм |
|
|
Wp |
0,2d33 (1 (d0 |
/ d3 )4 ) 0,2 603 1 0,84 25,5 103 ммз. |
|
|
3 |
|
|
|
Касательные напряжения на первом участке постоянны и равны
1 T1 / Wp1 0 .
13
На втором участке касательные напряжения зависят от диаметров d1 и d2. На первом подучастке второго участка при диаметре d1 касательные напряжения
|
|
1 |
T ' / W |
p |
|
100 103 |
/ 3,2 103 31 Н/мм2 31 МПа. |
||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
На втором подучастке второго участка при диаметре d2 |
|||||||||||||
|
|
|
' T ' / W |
p |
100 103 / 86,1 103 1 Н/мм2 1 МПа. |
||||||||
|
|
|
|
1 |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На первом подучастке третьего участка |
Н/мм2 2 МПа. |
||||||||||||
|
3 |
T ' |
/ W |
p |
|
150 103 |
/ 86,1 103 |
2 |
|||||
|
|
|
3 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
На втором подучастке третьего участка |
Н/мм2 6 МПа. |
||||||||||||
|
' |
T ' |
/ W |
p |
|
150 103 |
/ 25,5 103 |
6 |
|||||
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
На четвертом участке |
|
|
Н/мм2 10 МПа. |
||||||||||
|
4 |
T ' / W |
p |
250 103 |
/ 25,5 103 |
10 |
|||||||
|
|
|
4 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
По полученным значениям напряжений строим эпюру (рис. 4, |
|||||||||||||
в). Видно, |
|
что |
максимальное |
касательное |
напряжение в брусе |
||||||||
max 31 МПа. |
|
|
|
|
|
|
|
|
|
||||
Коэффициент запаса прочности S lim / max 90 / 31 3. Полярный момент инерции для полого круглого сечения бруса-
кольца (рис. 6) определяют по формуле
Ip Ip' Ip0 ((pd4)/32 (pd04)/32) (pd4 /32) (1 d0 / d)4) 0,1d4(1 (d0 / d)4).
Имеем:
при d1 d 30 мм
I |
p |
0,1d 4 (1 (d |
0 |
/ d )4 ) 0,1 304 |
(1 0,84 ) 4,8 104 |
мм4; |
|
|
|
1 |
1 |
|
|
||
|
1 |
|
|
|
|
|
|
при d2 |
3d 3 30 90 мм |
|
|
||||
I p2 0,1d2 |
4 (1 (d0 |
/ d2 )4 ) 0,1 904 (1 0,84 ) 387,4 104 мм4; |
|||||
при d3 2d 2 30 60 мм |
|
|
|||||
I p |
0,1d34 (1 (d0 |
/ d3 )4 ) 0,1 604 (1 0,84 ) 76,5 104 мм4. |
|||||
|
3 |
|
|
|
|
|
|
3. Определим перемещения сечений – углы поворота i на каждом силовом участке стержня:
на первом
1 (T1 l1 ) / (G I p1) 0 , т.к.Т1 0;
на втором
2 2 2 ,
14
где 2' – угол поворота подучастка с диаметром d второго участка, а2''– угол поворота на подучастке с диаметром 3d второго участка.
(T l ) / (G I |
p1 |
) (100 103 |
20,2 103 ) / (4 104 |
4,8 104 ) 2 10 2 |
рад, |
|||
2 |
2 2 |
|
|
|
|
|
|
|
(T l ) / (G I |
p2 |
) (100 103 2 0,2 103 ) / (4 104 387,4 104 ) 0,03 10 2 |
рад, |
|||||
2 |
2 2 |
|
|
|
|
|
|
|
2 2 10 2 0,02 10 2 2,03 10 2 рад;
на третьем
3 3 3 ,
где 3 '– угол поворота на подучастке с диаметром 3d третьего участка, а 3' '– угол поворота на подучастке с диаметром 2d,
(T l ) / (GI |
p |
) ( 150 103 2 0,2 103) / (4 104 387,4 104 ) 0,04 10 2 |
рад, |
|||||||||||||
3 |
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
'' (T |
l |
) / (G I |
|
p3 |
) ( 150 103 1 0,2 103 ) / (4 104 |
76,5 104 ) 0,1 10 2 |
рад, |
||||||||
3 |
3 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
0,04 10 |
2 |
0,1 10 |
2 |
0,14 10 |
2 |
рад; |
|
|
|
|
3 3 |
3 |
|
|
|
|
||||||||
на четвёртом
4 (T4 l4 ) / (G I p3 ) (250 103 0,2 103 ) / (4 104 76,5 104 ) 0,2 10 2 рад.
Построение эпюры углов сечений бруса начинают от защемления, где поворот защемлённого сечения 0. Тогда на границе тре-
тьего и четвертого участков угол поворота составит 4 0,2 10 2 рад. График представлен наклонной линией на четвёртом участке. На третьем участке в месте перехода диаметра 2d в диаметр 3d угол поворота сечения
4 3 0,2 10 2 0,1 10 2 0,1 10 2 рад.
На границе второго и третьего участков
4 3 3 0,2 10 2 0,1 10 2 0,04 10 2 0,06 10 2 рад.
На втором участке в месте перехода диаметра 3d в диаметр d
4 3'' 3' 2'' 0,2 0,1 0,04 0,03 10 2 0,09 10 2 рад.
На границе первого и второго участков
4 3 3 2 2 0,2 0,1 0,04 0,03 2 10 2 2,09 10 2 рад.
На первом участке угол поворота (закручивания) сечений постоянный:
4 3 3 2 2 1 0,2 0,1 0,04 0,03 2 0 10 2 2,09 10 2 рад.
График представлен прямой, параллельной базисной линии эпюры
15
(рис. 4, г). Угол закручивания свободного конца бруса 2,09 10 2 рад или 1,2 °.
3. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
Задание 3. 0пределить геометрические характеристики сечения сложной формы (рис. 6): а) площадь; б) моменты инерции относительно центральных осей; в) полярный момент; г) центробежный момент инерции; д) положение главных центральных осей; е) главные центральные моменты инерции; ж) главные центральные радиусы инерции.
Исходные данные для расчета приведены в табл. 3, где – угол поворота сечения против часовой стрелки от горизонтальной оси.
Таблица 3
Исходные данные к заданию 3
|
|
Числовые значения параметров по вариантам |
|
||||||||
Параметр |
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
10 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a, мм |
10 |
15 |
20 |
25 |
25 |
20 |
15 |
10 |
12 |
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
, град |
0 |
90 |
180 |
270 |
0 |
90 |
180 |
270 |
0 |
|
90 |
|
|
|
|
|
|
|
|
|
|
|
|
Указания по выполнению задания
1.Выбрать исходную систему координат х, у, вычислить относительно этих осей статические моменты сечения, найти центр тяжести сечения.
2.Провести через центр тяжести сечения оси xс , ус , параллельные
исходным.
3.Вычислить осевые, полярный и центробежный моменты относительно этих осей.
4.Определить положение главных центральных осей инерции u, v.
5.Вычислить значения главных центральных моментов инерции относительно осей u, v.
16
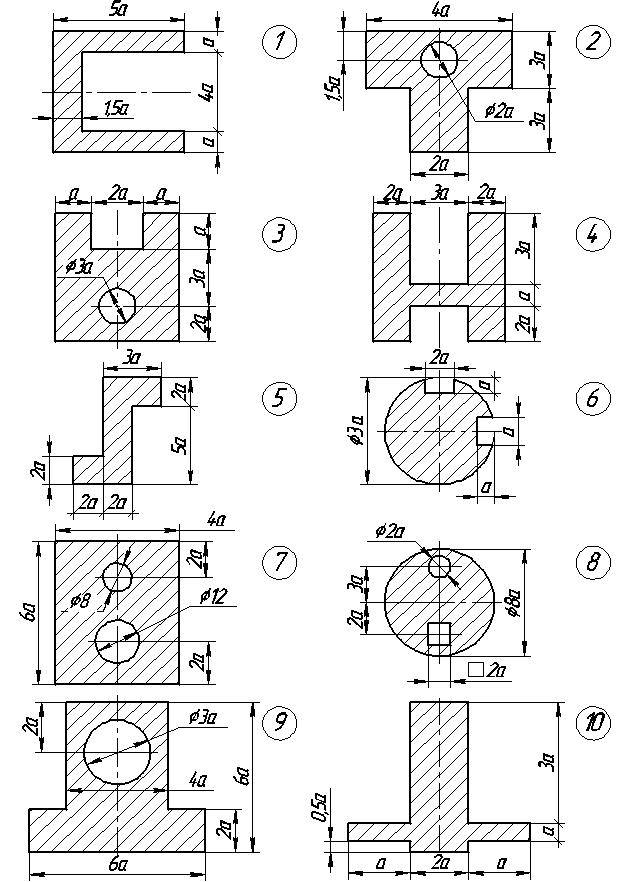
Рис. 6. Расчетные схемы плоских сечений к заданию 3. В кружках – номера вариантов
17

6.Рассчитать значения главных центральных радиусов инерции ru
иrv.
ПРИМЕР РАСЧЁТА |
|
||
Определить положение главных центральных осей инерции, зна- |
|||
чения главных центральных моментов инерции и радиусов инерции |
|||
сечения, изображенного на рис. 7, при а 20 мм. |
|
||
Решение |
|
|
|
1. Разобьём сложное сечение на три простых фигуры – два пря- |
|||
моугольника I и II, круг – III. Геометрические характеристики присо- |
|||
единяемых сечений фигур (прямоугольников I и II) складываются, а |
|||
вырезаемых (круг – III) – вычитаются. |
|
|
|
Определяем площадь сечения |
|
|
|
A Ai A1 A2 A3 20 60 40 60 3,14 202 / 4 3286 мм2. |
|||
Выбираем исходную систему координат х, у. В этой системе ко- |
|||
ординат находим положение центров тяжести простых фигур. Для |
|||
прямоугольника I – С1 |
|
|
|
( х1 10 мм, y1 30 мм), для прямоугольника II – |
С2 ( х2 60 мм, |
||
|
у2 |
20 мм), |
для круга III – |
|
С3 ( х3 60 мм, у3 20 мм). |
||
|
Через центры тяжести про- |
||
|
стых фигур |
проводим оси |
|
|
координат – их центральные |
||
|
оси инерции. |
||
|
2. Вычислим статические |
||
|
моменты сечения: |
||
|
|
относительно оси х |
|
|
Sx Ai yi A1y1 A2 y2 A3 y3 |
||
|
1200 30 2400 20 314 20 |
||
|
90280 мм2; |
|
|
Рис. 7. Расчётное сечение |
|
относительно оси у |
|
Sy |
Ai xi A1x1 A2x2 A3x3 |
||
1200 810 2400 60 314 60 174840 мм2 |
|
|
|
3. Определим координаты центра тяжести фигуры: |
|||
18
xc Sy / A Ai xi / A 174840 / 3286 44,7 мм; yc Sx / A Ai yi / A 90280 / 3286 23,1 мм.
Проводим параллельно исходным осям x и у через центр тяжести сечения С с координатами (44,7; 23,1) центральные оси координат xс
и ус.
4. Вычислим моменты инерции относительно центральных осей xс и yс.
Момент инерции сечения относительно оси xс
|
|
|
Ix IxI |
|
|
IxII |
IxIII , |
|
|||
|
|
|
c |
c |
|
|
c |
|
c |
|
|
где IxI , |
IxII , |
IxIII |
- моменты инерции простых сечений I, II, III относи- |
||||||||
c |
c |
c |
|
|
|
|
|
|
|
|
|
тельно оси xс. |
|
|
|
|
|
|
|
|
|
||
Расчёт момента инерции IxI |
выполняем по формуле |
|
|||||||||
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
I I |
I |
x |
a 2 A . |
|
||||
|
|
|
x |
|
|
1 |
1 |
|
|||
|
|
|
c |
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
Момент инерции прямоугольника I относительно собственной |
|||||||||||
центральной оси xс |
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
|
|
|
|
|
|
мм4. |
|
|
Ix |
b· h3 /12 a· (3a)3 /12 27 а4 /12 36 104 |
||||||||
|
|
c1 |
|
|
|
|
|
|
|
|
|
Расстояния между осями xс |
и хc |
|
|
|
|
||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
a1 y1 yc |
30 23,1 6,9 мм. |
|
||||||
Площадь прямоугольника I |
|
|
|
|
|
|
1200 мм2. |
|
|||
|
|
|
A 3а а За2 |
|
3 202 |
|
|||||
|
|
|
1 |
|
|
|
|
|
|
|
|
Значение момента инерции относительно оси xс |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
IxI 36 104 6,92 |
|
1200 |
417132 мм4 . |
|
||||
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
Аналогично для прямоугольного сечения II |
|
||||||||||
|
|
|
I II |
I |
x |
|
a 2 A ; |
|
|||
|
|
|
x |
|
|
|
2 |
2 |
|
||
|
|
|
c |
|
|
c2 |
|
|
|
|
|
момент инерции прямоугольника II относительно собственной цен- |
|||||||||||
тральной оси xс |
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
|
|
|
|
|
|
мм4; |
|
|
Ix |
b· h3 /12 3a·(2a)3 |
|
/12 24а4 /12 32 104 |
||||||
|
|
c2 |
|
|
|
|
|
|
|
|
|
расстояния между осями xс и хc |
|
|
|
|
|
|
|
||||
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
a2 y2 yc |
20 23,1 3,1 мм; |
|
||||||
площадь прямоугольника II |
|
|
|
|
|
|
2400 мм2; |
|
|||
|
|
|
A 3а 2а 6а2 |
|
6 202 |
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|
|
19
IxII 32 104 3,1 2 2400 731864 мм4.
c
Момент инерции сечения круга III относительно оси xс:
I III I |
x |
a |
2 A ; |
x |
3 |
3 |
|
c |
c3 |
|
|
Ixc3 d 4 / 64 3,14 204 / 64 7850 мм4; a3 y3 yc 20 23,1 3,1 мм;
A3 p d 2 / 4 3,14 202 / 4 314 мм2; IxcIII 7850 3,12 314 61735мм4.
Величина момента инерции сечения относительно оси xс Ixc 417132 343064 10867 749329мм4.
5. Момент инерции сечения относительно оси ус
|
|
Iy IyI |
|
IyII |
IyIII , |
|||
|
|
c |
c |
|
|
c |
|
c |
где IyI , |
IyII , |
IyIII - моменты инерции простых сечений I, II, III относи- |
||||||
c |
c |
c |
|
|
|
|
|
|
тельно оси ус. |
|
|
|
|
|
|
||
Момент инерции IycI рассчитываем по формуле |
||||||||
|
|
I I |
I |
y |
b 2 A . |
|||
|
|
y |
|
|
1 |
1 |
||
|
|
c |
|
|
c1 |
|
|
|
Момент инерции прямоугольника I относительно собственной |
||||||||
центральной оси yс |
|
|
|
|
|
|
||
|
|
1 |
|
|
|
/12 а4 / 4 4 104 мм4. |
||
|
|
Iyc h· b3 /12 3a a3 |
||||||
|
|
1 |
и yс |
|
|
|||
Расстояния между осями yс |
|
|
||||||
|
|
1 |
|
|
|
|
|
|
|
|
b1 x1 xc 10 44,7 34,7 мм. |
||||||
Площадь прямоугольника I |
A 1200 мм2. |
|||||||
|
|
|
1 |
|
|
|
|
|
Величина момента инерции относительно оси ус |
||||||||
|
|
IycI 4 104 34,7 |
2 1200 1484908 мм4 . |
|||||
Аналогично для прямоугольника II: |
|
|
||||||
|
|
I II |
I |
y |
b |
2 A ; |
||
|
|
y |
|
|
c 2 |
2 |
2 |
|
|
|
c |
|
|
|
|
|
|
|
Iy |
hb3 /12 2a (3a)3 |
/12 4,5а4 4,5 204 72 104 мм4; |
|||||
|
c 2 |
b2 x2 xc |
60 44,7 15,3 мм. |
|||||
|
|
|||||||
|
|
IyII 72104 15,3 2 |
2400 1281816 мм4. |
|||||
|
|
c |
|
|
|
|
|
|
Момент инерции круга относительно оси yс:
20
