задачи из банка с решен.№1-№14

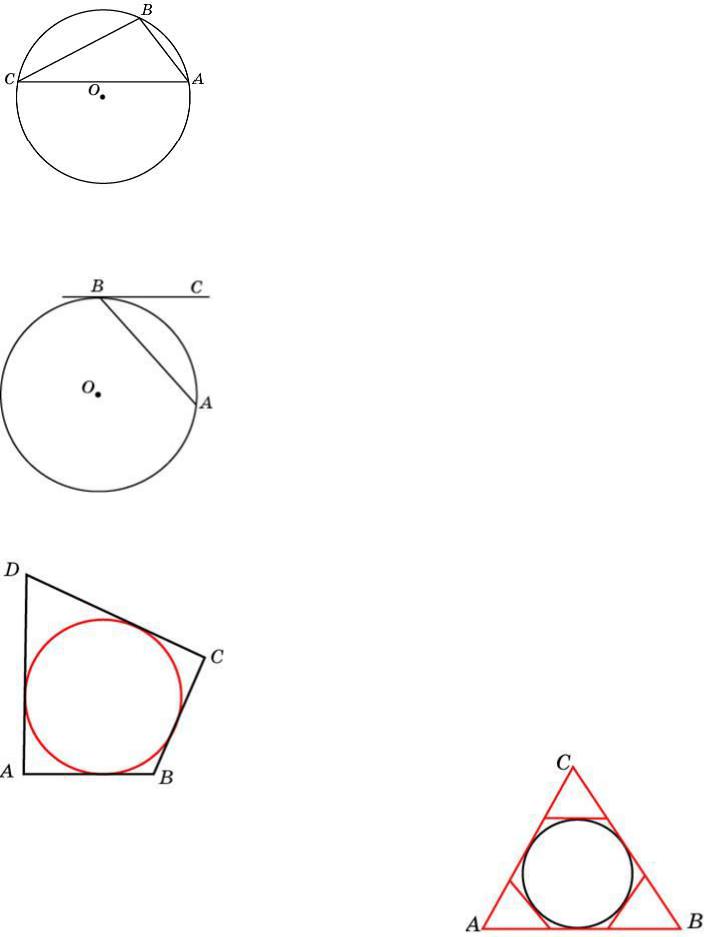
Задание №27868

Точки A, B, C, расположенные на окружности, делят ее на три дуги, градусные величины которых относятся как 1:3:5. Найдите больший угол треугольника ABC. Ответ дайте в градусах.

Если ввести коэффициент пропорциональности k, то дуги в сумме образуют окружность 9k.

Мы знаем, что градусная мера дуги, длиною в окружность, равна 360°. Тогда k 40° Понятно также, что больший угол треугольника лежит против большей дуги. Тогда незамедлительно, больший угол треугольника равен половине градусной меры дуги окружности, на которую он опирается, и равен 5k/2 100°.

Ответ: 100.

Задание №27877

Хорда AB стягивает дугу окружности в 92°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.

Угол между касательной и хордой равен половине градусной меры дуги, которую этот угол стягивает.

Ответ: 46.

Задание №27941

В четырехугольник ABCD вписана окружность, AB=10, BC=11 и CD 15. Найдите четвертую сторону четырехугольника.

Суммы длин противоположных сторон четырехугольника равны, если в него можно вписать окружность. Этот факт можно получить на основе того, что отрезки двух касательных, исходящих к окружности из одной точки, равны.

Ответ: 14.

Задание №27943

К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.

Только лишь на свойстве касательных, проведенных из одной точке к окружности, можно понять, что периметр

121

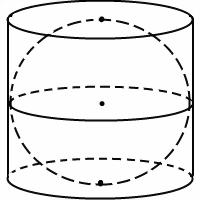
большого треугольника будет равен сумме периметров маленьких.

Ответ: 24.

Задание №284348

В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SO=4, AC 6. Найдите боковое ребро SC.

Точка О является центром основания правильной четырехугольной пирамиды, а значит образуется прямоугольный треугольник, гипотенузой в котором является искомое боковое ребро, одним катетом – высота пирамиды, а другим – половина диагонали основания.

Ответ: 5.

Задание №316552

В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB=24, AD=10, AA1 22. Найдите площадь сечения, проходящего через вершины A, A1 и C.

Это сечение представляет собой прямоугольник АА1С1С. Нужно только отыскать сторону АС, по теореме Пифагора, находим АС=26.

Ответ: 572.

Задание №316554

В кубе ABCDA1B1C1D1 найдите угол между прямыми AD1 и B1D1. Ответ дайте в градусах.

Треугольник AD1B1 равносторонний, каждая его сторона является диагональю соответствующей грани куба.

Ответ: 60.

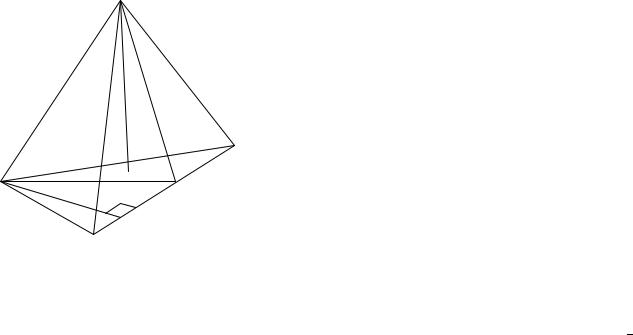
Задание №316557 Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной

поверхности цилиндра. Площадь поверхности шара

шар 4

.

Площадь полной поверхности цилиндра

ц

бок 2 осн 2

2

2 (

).

Поскольку цилиндр вписан в шар, то высота цилиндра равняется двум радиусам.

	2 (2	)	6	3			166,5.
						шар
				2

Ответ: 166,5.

Задание №316558

В правильной треугольной призме ABCA1B1C1, все ребра которой равны 3, найдите угол между прямыми AA1 и BC1. Ответ дайте в градусах.

Правильная призма это прямая призма, в основаниях которой правильные многоугольники.

Поскольку ребро АА1 параллельно ребру СС1, то искомый угол это просто угол СС1В. Поскольку все ребра равны, то грани призмы есть квадраты, а значит искомый угол равен 45 градусов.

Ответ: 45.

122

Задание №317338

Площадь параллелограмма ABCD равна 189. Точка E — середина стороны AD. Найдите площадь трапеции AECB.

Если а – сторона ВС параллелограмма, то его площадь и искомая площадь связаны

						3
п	,				2			141,75.
		2	2			4

Ответ: 141,75.

Задание №318145 В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём жидкости

равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

Объемы подобных тел относятся как кубы коэффициента подобия. Если объем жидкости равен 70 мл, то весь сосуд вместит в 8 раз больше, 560, значит долить осталось 490 мл.

Ответ: 490.

Задание №318146

В правильной четырёхугольной пирамиде SABCD с основанием ABCD боковое ребро SA равно 5, сторона основания равна 3 2. Найдите объём пирамиды.

Нужно найти высоту. Половина диагонали основания по, теореме Пифагора, из равнобедренного прямоугольного треугольника в основании получается равной 3, а уже из треугольника, плоскость которого перпендикулярна плоскости основания, с гипотенузой в виде ребра, одним катетом которого является половина диагонали основания, а другим – высота, получаем, что высота равна 4.

Площадь основания равна квадрату стороны, 6. Тогда искомый объем 1/3 6 4=8.

Ответ: 8.

Задание №47995

В треугольнике ABC угол A равен 60°, угол B равен 53°. AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.

Можно найти

180°	180° 60°	1	120°	1	(180°	) 86,5°.
		2		2

Теперь, из треугольника AFO, можно найти искомый угол.

180°	93,5°	1	63,5°.
		2

Ответ: 63,5.

123

Задание №71889 Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого

равны 15. Найдите объем параллелепипеда.

Для начала, окружность не впишешь в прямоугольник, значит в основании нашего параллелепипеда лежат квадраты, причем сторона любого из них равна двум радиусам. Тогда сразу объем параллелепипеда 15 30 30=13500.

Ответ: 13500.

Задание №71929 Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен

12. Объем параллелепипеда равен 115,2. Найдите высоту цилиндра.

х (2 12) (2 12)=115,2, х=0,2.

Ответ: 0,2.

Задание №71969 Куб описан около сферы радиуса 12,5. Найдите объём куба.

Ребро куба в два раза больше радиуса шара, в него в писанного, 2 12,5 25. Формулу объема куба мы знаем.

Ответ: 15625.

Задание №72539 Площадь поверхности куба равна 200. Найдите его диагональ.

Диагональ куба в корень из трех раз больше его ребра, а площадь поверхности равна 6 а2.

Ответ: 10.

Задание №72601 Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона

основания которой равна 5, а высота — 5.

Площадь боковой поверхности правильной призмы, это произведение периметра основания на высоту.

Ответ: 150.

Задание №72673 Радиус основания цилиндра равен 7, высота равна 10. Найдите площадь боковой поверхности цилиндра, деленную на .

Мы знаем формулу площади боковой поверхности цилиндра, её можно получить в домашних условиях. Сверните прямоугольный лист трубочкой так, чтобы границы лишь соприкасались – получили боковую поверхность цилиндра. Пусть теперь радиус основания равен R, высота цилиндра h. Мы знаем, как посчитать длину окружности, 2 R. Теперь разворачивайте ваш прямоугольный лист – получите ту же поверхность, которая является прямоугольником со сторонам 2 R и h, её площадь равна произведению 2 Rh.

Ответ: 140.

124

Задание №72719 Площадь большого круга шара равна 7. Найдите площадь поверхности шара.

Площадь поверхности шара в 4 раза больше площади большого круга, есть соответствующая формула.

Ответ: 28.

Задание №72871 Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с

диагоналями, равными 9 и 40, и боковым ребром, равным 55.

Площадь ромба можно найти еще и как произведение его диагоналей. Ну, а площадь поверхности призмы мы считать умеем.

Ответ: 19800.

Задание №73123 Через среднюю линию основания треугольной призмы, площадь боковой поверхности

которой равна 54, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.

Площади подобных фигур относятся как квадраты коэффициента подобия. Каждую грань обеих призм можно рассматривать как фигуру – они будут образовывать пары подобных треугольников с коэффициентом 0,5. Т.е. площадь боковой поверхности отсеченной треугольной призмы будет в 4 раза меньше площади большой призмы.

Ответ: 13,5.

Задание №75173 Объем треугольной пирамиды равен 30. Плоскость проходит через сторону основания этой

пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 7:8, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.

Очень интересная ситуация, рисунка к этой задаче нет, а без него её не решить.

	S		Придется рисовать самому.
			Итак, на рисунке плоскость ASD разбивает
			пирамиду на две, причем CD : BH=7:8.
			Специально для наглядности проведены высота
			большой пирамиды и высота треугольника АВС.
			Это сделано для удобства рассмотрения пирамид
		C	SABD и SACD.
A	P		Высота у них одна и та же, SP. У оснований-
	D		треугольников тоже одна высота, АН, а вот длины
	H		сторон, к которым она проведена, разные. Зато в
			условии задачи дано отношение этих сторон.
	B		Значит, мы можем узнать отношение площадей
			треугольников ABD и ACD, оно равно отношению

сторон, к которым проведены равные высоты, т.е. равно 8:7.

Постепенно становится понятно, что большим объёмом обладает пирамида SABD. Давайте введем площадь S треугольника ABD и SP=h, тогда площадь треугольника ACD будет равна .

125

Объем пирамиды SABD будет равен		, объем пирамиды SACD будет равен								.
Тогда объем исходной пирамиды будет равен						30, откуда искомый объем пирамиды
SABD равен 30 8/15=16.

Каждому должно быть понятно, что пирамида абсолютно произвольная, никаких хороших свойств, кроме обусловленных задачей, нам здесь не потребовалось. Только простые рассуждения и проведения высот, не требующие каких-либо доказательств.

Многим читателям покажется, что рисунок мой неправильный, что плоскость проходит не через сторону основания, а через ребро пирамиды, и что вершина никакая не вершина, а точка основания пирамиды. Это всё неверно, поскольку что именно назвать вершиной пирамиды, а что её основанием – дело сугубо личное. Рисунок я рисовал именно так, потому что счел максимально наглядным и понятным именно такое расположение секущей плоскости.

Ответ: 16.

Минимум:

1)надо знать всё про прямоугольный параллелепипед, про его частный случай – куб

2)надо знать всё про прямоугольный треугольник, теорему Пифагора надо знать

3)надо знать хотя бы одну формулу площади треугольника

4)надо уметь вычислять все элементы треугольника по нескольким данным – теоремы косинусов и синусов.

Необходимый уровень:

1)знать всё про треугольник, окружность, параллелограмм (и все его частные случи – ромб, прямоугольник, квадрат), трапецию – множество свойств и формул, описывающих отношение между элементами

2)многочисленные формулы площадей плоских фигур, уметь выводить формулы искомых элементов – как мы сами вывели формулу расстояния между серединами диагоналей трапеции

3)знать всё про многоугольник, вписанный в окружность или описанный около неё

4)знать всё про секущие, касательные, хорды, вписанные и центральные углы, дуги, сектора и сегменты

5)знать всё про призму (частный случай – прямоугольный параллелепипед, куб), пирамиду, конус, сферу – многочисленные формулы объемов, площадей полных поверхностей, площадей боковых поверхностей, знать случаи их взаимного расположения (что-то во что-то вписано), а также уметь уверенно строить сечения чего-то плоскостью

6)обязательно надо знать все приемы координатного и векторного методов – формулы расстояния между точками, координат середины отрезка, длины вектора, косинуса угла между векторами, уравнения прямой по двум точкам и так далее

126

ПРОТОТИПЫ ЗАДАНИЙ 5 (КОМБИНАТОРИКА)

Для решения предложенных задач не нужно много теории. Большинство задач решаются просто делением числа благоприятных (или неблагоприятных) исходов на число всех исходов.

Но есть и невообразимо трудные задачи, которые никогда не решатся без специальных знаний по теории вероятностей – иные даже я не мог решить. В общем, не стоит недооценивать задачи на теорию вероятностей.

Великое множество предложенных в разделе задач дублируется в ранее разобранных – очень много задач из "Алгебры" и "Функций".

Задание №2675db

Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 7, но не дойдя до отметки 1.

Участок от отметки 7 до отметки 1 занимает ровно половину круга циферблата. Ответ должен быть понятен каждому – уж либо часовая стрелка на одной половине, либо нет – 2 исключающих друг друга варианта.

Ответ: 0,5.

Задание №282853 В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что

сумма выпавших очков равна 8. Результат округлите до тысячных.

Число всех вариантов равно 62 36, потому что у игральной кости 6 граней с числами от 1 до 6, а в условии задачи игральных костей две, поэтому возводим 6 в квадрат.

Теперь нужно число 8 представить в виде двух слагаемых от 1 до 6 – найти число благоприятных исходов.

2+6=8; 6+2=8; 3+5=8; 5+3=8; 4+4=8 – всего 5 вариантов.

Осталось поделить 5 на 36 аккуратно в столбик, получить 4 знака после запятой (получать больше знаков смысла нет!) чтобы можно было округлить результат до тысячных, т.е. до третьего знака после запятой.

5

36 0,1388. Данный результат легко округляется до тысячных.

Ответ: 0,139.

Задание №282854 В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того,

что орел выпадет ровно один раз.

Давайте распишем все возможные результаты. Причем результаты орел, решка и решка, орел считаются за 2 разных результата.

Решка, решка решка, орел орел, орел орел, решка.

Всего 4 уникальных варианта, среди которых есть только 2 варианта, удовлетворяющих условию задачи. Искомая вероятность 2:4 0,5.

Ответ: 0,5.

127

Задание №282855 В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные —

из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.

Поскольку порядок участия выбирается жребием – случайным образом – то вопрос можно со всей уверенностью переиначить: найдите вероятность того, что случайно выбранная наугад гимнастка окажется из Китая.

Каждый читатель должен осознать, что это действительно так.

Тогда искомая вероятность найдется делением числа китайских гимнасток на общее число атлетов.

Ответ: 0,25.

Задание №282856 В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите

вероятность того, что один случайно выбранный для контроля насос не подтекает. Просто разделим число не подтекающих насосов на общее число. (1000–5):1000=0,995.

Ответ: 0,995.

Задание №283443 В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что

сумма выпавших очков равна 16. Результат округлите до тысячных.

Всего вариантов 63 216, потому что у игральной кости 6 граней с числами от 1 до 6, а всего в задаче 3 кости, поэтому 6 возводим в третью степень.

Теперь нужно представить 16 в виде суммы трех слагаемых от 1 до 6 – посчитать число благоприятных исходов.

6+6+4=16; 6+4+6=16; 4+6+6=16; 5+5+6=16; 5+6+5=16; 6+5+5=16 – всего 6 вариантов.

Осталось поделить в столбик 6 на 216, получить 4 знака после запятой и результат округлить до тысячных, т.е. до третьего знака после запятой.

6	1		0,0277.
216	36

Ответ: 0,028.

Задание №283467 В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность

того, что орел выпадет ровно два раза.

Всего вариантов 23 8, потому что у монеты есть две стороны, а всего бросков 3, поэтому 2 возводим в степень 3.

Теперь посчитаем число благоприятных исходов: решка, орел, орел орел, решка, орел орел, орел, решка – всего 3 варианта.

Осталось поделить 3 на 8.

Ответ: 0,375.

128

Задание №283727 В соревнованиях по толканию ядра участвуют 3 спортсмена из Македонии, 8 спортсменов из

Сербии, 3 спортсмена из Хорватии и 6 — из Словении. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Сербии.

Поскольку порядок выступления определяется жребием – случайным образом – то вопрос можно переформулировать без потери качества: найдите вероятность того, что наугад выбранный спортсмен окажется из Сербии.

Делим 8:20 0,4.

Ответ: 0,4.

Задание №285922 Научная конференция проводится в 5 дней. Всего запланировано 75 докладов — первые три

дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. На конференции планируется доклад профессора М. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?

Найдем количество докладов, запланированных на последний день конференции.

(75–17–17–17):2=12.

Любой из 12 докладов последнего дня конференции может быть докладом профессора Мориарти – это и есть число благоприятных исходов. Осталось 12 поделить на 75. Вообще если в задании ЕГЭ идет речь о некоем профессоре М, то это всегда профессор Мориарти.

Ответ: 0,16.

Задание №286207 Перед началом первого тура чемпионата по настольному теннису участников разбивают на

игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 спортсменов, среди которых 13 спортсменов из России, в том числе Владимир Егоров. Найдите вероятность того, что в первом туре Владимир Егоров будет играть с каким-либо спортсменом из России.

Соперником Владимира Егорова может быть любой из 25 спортсменов, не 26,. потому что сам Владимир Егоров сам с собой играть не может. Нам нужно, чтобы этот любой был спортсменом из России – 12 благоприятных исходов, не 13, потому что Владимир Егоров сам из России.

Ответ: 0,48.

Задание №286325 В сборнике билетов по философии всего 50 билетов, в 11 из них встречается вопрос по теме

"Пифагор". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопрос по теме "Пифагор".

(50–11):50=0,78.

Ответ: 0,78.

Задание №286385 На чемпионате по прыжкам в воду выступают 20 спортсменов, среди них 6 прыгунов из

Германии и 10 прыгунов из США. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что одиннадцатым будет выступать прыгун из Германии.

129

Представим ситуацию – вы должны выбрать из урны с 20-ю номерками с числами от 1 до 20 какой-то один номерок. Вероятность того, что выбранный вами номерок будет 11, или 7, или 19 будет ровно одна и та же – 1:20=0,05 – поэтому можно просто спросить: найдите вероятность того, что случайно выбранный прыгун будет из Германии.

6:20=0,3.

Ответ: 0,3.

Задание №319355 Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью

0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

Здесь всё просто. Какова вероятность победы в первой партии? 0,52. А во второй? 0,3 (если поменять очередность игровых цветов, то наоборот). Нам нужно две победы подряд, значит нужно перемножить вероятности 0,52 0,3=0,156.

Если события А и В независимы, причем вероятности этих событий известны, то вероятность совместного события А и В равна произведению их вероятностей.

Ответ: 0,156.

Задание №319353 Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика

выпускает 45% этих стекол, вторая –– 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая –– 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Пусть в магазине 10000 (это число взято исключительно для удобства умножения на сотые доли, строго говоря, можно было взять абсолютно любое число) стёкол. Тогда от первой фирмы 5500 стекол, среди которых ровно 0,03 5500 165 бракованных от второй фирмы будет 4500 стекол, среди которых ровно 45 бракованных.

Итак, всего стекол 10000, из них бракованных 165 45 210. Искомая вероятность

210:10000=0,021.

Ответ: 0,021.

Задание №320169 Вася, Петя, Коля и Лёша бросили жребий — кому начинать игру. Найдите вероятность того,

что начинать игру должен будет Петя. Все четыре человека равноправны, 0,25.

Ответ: 0,25.

Задание №320170 В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре

группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп:

1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.

Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?

Из 16 карточек четыре с номером 2 – из 16 возможных исходов четыре благоприятных. 4:

16=0,25.

130