выч.математика - Башуров

		Теперь применяем обратный ход: x =			4,77	= 34,07 ;
			3		0,14
x	=	-3,52 +1,34 ×34,07	=18,81; x =	3, 2 - 0, 6 ×34,07 +1,3 ×18,81			= 3, 43.
2		2, 24	1			2,1

Округляя, получаем ответ: x1 = 3, 4; x2 =18,8; x3 = 34,1.

Ниже представлено решение данной системы методом Гаусса с помощью пакета Mathcad, которое дает следующий результат: x1 = 3,323; x2 =17,978 ;

x3 = 32, 655.

Также систему можно решить через блок Given-Find:

3. Интерполяция функций

На практике возникает задача приближения функции. Например, в неко-

торых точках x0 , x1 ,..., xn		известны значения функции f (x): y0 , y1 ,..., yn , не-
обходимо определить значения функции f (x)				при других значениях x . Связь
y = f (x)	неизвестна.	Возможна	другая	ситуация, когда	зависимость
y = f (x)	известна, но она может быть очень сложной или требовать громозд-

ких вычислений. Поэтому целесообразно вычислить ее значения в отдельных точках, а в других точках вычислять по каким-либо простым формулам.

Перечисленные задачи являются задачамиаппроксимации (приближения функции). В первом случае возникает задача точечной аппроксимации, во

втором – задача непрерывной аппроксимации. При этом функцию f (x) тре-

буется приближенно заменить (аппроксимировать) некоторой функцией φ (x)

10

так, чтобы отклонение φ (x) от f (x) в заданной области было наименьшим.

Функция φ (x) при этом называется аппроксимирующей.

Одним из типов аппроксимации являетсяинтерполяция, когда φ (x)

проходит через все точки (xi ; yi ). Обычно интерполяционные функции стро-

ятся в виде многочленов φ (x) = a0 + a1x + ... + an xn . Коэффициенты ai функ-

ции φ (x) определяются из условия совпадения yi = φ (xi ). Точки xi называ-

ются узлами интерполяции. Интерполяционные кривые могут строиться -от дельно для разных частей заданного интервала – такая интерполяция называется локальной. Если строится одна функция на всем интервале, то это глобальная интерполяция.

Рассмотрим глобальную интерполяцию в виде алгебраического много-

члена φ (x) = a	+ a x + ... + a xn . Для нахождения коэффициентов a необхо-
0	1	n				i
димо решить систему алгебраических уравнений
	ì		2	n
		+ a1 x0 + a2 x0		+... + an x0	= y0 ;
	ïa0
	ï a	+ a x + a x2		+... + a xn	= y ;
	í 0	1 1	2 1	n 1	1
	ï		...
	ïa	+ a x	+ a x2	+ ... + a xn = y		.
	î 0	1 n	2 n	n n	n

Получили систему n +1 линейных уравнений сn +1 неизвестными. Удобство применения многочленов при интерполяции состоит том, что для нахождения коэффициентов многочлена приходится решать систему линейных уравнений. Если в качестве интерполирующей функции выбрать какую-либо другую функцию, то придется решать систему нелинейных уравнений, а это более сложная задача.

Иногда нет необходимости определять коэффициенты многочлена, а надо лишь найти значения функции в промежуточных точках. В этом случае удобно использовать интерполяционный многочлен в форме Лагранжа. Мно-

гочлен в форме Лагранжа записывается в виде:

L

(x) = y

(x - x1 )(x - x2 )...(x - xn )

+ y

(x - x0 )(x - x2 )...(x - xn )

+

0 (x

- x

)(x

- x )... (x

- x

)

- x

)(x

- x

)... (x

- x

)

n

n

1 (x

0

1

0

2

0

1

0

1

2

1

n

+... + yn

(x - x0 )...(x - xn-2 )(x - xn-1 )

(x

- x

)... (x

- x

)(x

- x

)

n

0

n

n-2

n

n-1

или в общем виде:

11

Ln	(x) = å yi ×	Õ (x - x j ) .
	n	n
	i=0	j=0, j¹i	(xi - x j )

Для большого числа узлов удобно использоватьинтерполяционный мно-

гочлен в форме Ньютона. Он имеет следующий вид:

Pn (x) = c0 + c1 (x - x0 )+ c2 (x - x0 )(x - x1 )+ ... + cn (x - x0 )...(x - xn-1 ),

где коэффициенты ci последовательно вычисляют из условий совпадения зна-

чений многочлена Pn (x)		в узлах		интерполяции			с соответствующими значе-
ниями yi .
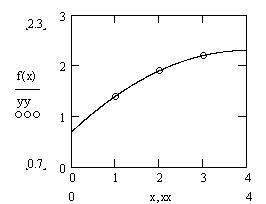
Пример. Задана табличная функция
	x		1		2		3
	y		1,4		1,9		2,2

Найдем интерполяционный многочлен в общем виде, в форме Лагранжа, в форме Ньютона и с их помощью определим значение в точке x =1,5.

Решение. Составим систему уравнений:

ìï a0 ía0 ïîa0

+a1 ×1 + a2 ×12 =1, 4;

+a1 × 2 + a2 × 22 =1,9;

+a1 ×3 + a2 ×32 = 2,2.

Решим ее методом Гаусса. Умножаем первое уравнение на (-1) и скла-

дываем сначала со вторым, а потом с третьим уравнениями. Получаем:

ìa		+a	+a	=1, 4;
ï	0	1	2	= 0,5;
í		a1	+3a2
ï		2a1	+8a2	= 0,8.
î

Умножаем второе уравнение на (-2) и складываем с третьим:

ìa		+a	+a	=1, 4;
ï	0	1	2	= 0,5;
í		a1	+3a2
ï			2a2 = -0, 2.
î

12

Через обратный ход получаем a2 = -0,1; a1 = 0,8; a0 = 0, 7 . В результа-

те получаем интерполяционный многочленφ (x) = 0,7 + 0,8x - 0,1x2 . Нахо-

дим значение в точке x =1,5: φ (1,5) =1, 675 »1,7 .

Теперь составим интерполяционный многочлен в форме Лагранжа:

L	(x) =1, 4 (x - 2)(x - 3)	+1,9	(x -1)(x - 3)		+ 2, 2	(x -1)(x - 2)	=
2	(1- 2)(1 - 3)	(2		-1)(2 - 3)		(3 -1)(3 - 2)
	= 0,7(x - 2)(x - 3) -1,9(x -1)(x - 3) +1,1(x -1)(x - 2).
Находим значение в точке x =1,5				:
L2 (1,5) = 0,525 +1, 425 - 0, 275				= 1, 675 »1, 7 .

Определим интерполяционный многочлен в форме Ньютона:

P2 (x) = c0 + c1 (x -1)+ c2 (x -1)(x - 2).

Подставляем первую точку табличной функции, получаем

1, 4 = c0 Þ c0 =1, 4 .

Подставляем вторую точку табличной функции, получаем

1,9 =1, 4 + c1 (2 -1)Þ c1 = 0,5 .

Подставляем третью точку табличной функции, получаем

2, 2 =1, 4 + 0, 5(3 -1) + c2 (3 -1)(3 - 2)Þ =c1 -0,1.

В результате получаем многочлен в форме Ньютона:

P2 (x) =1, 4 + 0,5(x -1)- 0,1(x -1)(x - 2).

Находим значение в точке x =1,5:

P2 (1,5) =1, 4 + 0, 25 + 0,025= 1, 675 »1, 7 .

Рис. 1. Точки табличной функции и график интерполяционного многочлена

Итак, различные формы интерполяционного многочлена отличаются друг от друга лишь способом организации вычислений. Сам многочлен (при отсутствии совпадающих узлов) полностью определяется таблицей.

13

Для интерполяционного многочлена в форме Ньютона имеет значение, в каком порядке производить вычисления. Записанный выше многочлен удобен для нахождения значений функции от аргументов, близких к x0 , за ним закрепилось название «многочлен для интерполирования вперед». При вычислении значений функции от аргументов, близких к xn , многочлен Ньютона удобнее составлять в следующем виде:

Pn (x) = c0 + c1 (x - xn ) + c2 (x - xn )(x - xn-1 ) + ... + cn (x - xn )...(x - x1 ),

который называют многочленом «для интерполирования назад». Вычисления коэффициентов необходимо делать подставлением точек табличной функции

от (xn ; yn ) к (x0 ; y0 ). Разумеется, оба названия весьма условны, и различия

между формулами сказываются лишь при разовых вычислениях. После выполнения всех преобразований они приводят к одному и тому же многочлену(при отсутствии совпадающих узлов таблицы).

При локальной интерполяции для каждого интервала строится своя функция с использованием значений соседних точек. Заданы узлы x0 , x1 ,..., xn , из-

вестны значения функции f (x) в узлах: y0 , y1 ,..., yn . Используя уравнение прямой на i-том интервале, проходящей через точки (xi-1; yi-1 ) и (xi ; yi ), по-

лучаем следующую формулу линейной интерполяции:

y = yi-1 + ( yi - yi-1 ) x - xi-1 . xi - xi-1

По этой формуле можно определить значение f (x) в любой точке ин-

тервала (xi-1; xi ). Для более точных локальных вычислений строится квадра-

тичная интерполяция, когда значение f (x) в любой точке интервала (xi-1; xi )

находится, используя три точки

y = yi-1 + ( yi - yi-1 ) x - xi-1 xi - xi-1

(xi-1; yi-1 ), (xi ; yi ) и (xi+1; yi+1 ):

+ ( yi+1 - 2 yi + yi-1 )	(x - xi-1 )(x - xi )
				.
	2(x - x	)(x	- x )
	i i-1	i+1	i

Замечание. В настоящее время наиболее широко распространены кубические сплайны – многочлены третьей степени, гладко состыкованные в узлах интерполяции.

14

С помощью пакета Mathcad можно построить обычный интерполяционный многочлен, сплайн, линейную локальную интерполяцию и вычислить значения в промежуточных точках.

Пример. Заданы экспериментальные точки в виде табличной функции

W (U ) :

Формируем матрицу коэффициентов системы и находим их методом Га-

усса:

Формируем интерполяционный многочлен и с его помощью найдем значение в промежуточной точке U = 230 :

Изобразим экспериментальные точки вместе с интерполяционным многочленом на одном чертеже (рис. 2).

15

Рис. 2. Экспериментальные точки и график интерполяционного многочлена

Сформируем сплайн и также с его помощью найдем значение в промежуточной точке U = 230 :

Изобразим экспериментальные точки и сплайн (рис. 3).

Рис. 3. Экспериментальные точки и сплайн

Построим локальную линейную интерполяцию и также с его помощью найдем значение в промежуточной точке U = 230 :

Изобразим экспериментальные точки и график линейной интерполяции

(рис. 4).

16

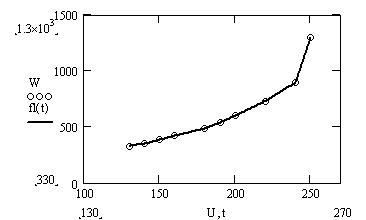
Рис. 4. Экспериментальные точки и график линейной интерполяции

4. Метод наименьших квадратов

При интерполировании основным условием является прохождение графика интерполяционной функции (многочлена) через данные значения функ-

ции f (x) в узлах интерполяции. Однако в ряде случаев выполнение этого ус-

ловия затруднительно или даже нецелесообразно. Например, при большом количестве узлов получается высокая степень интерполяционного многочлена в случае глобальной интерполяции. Кроме того, данные могут быть получены из эксперимента и содержать ошибки. Построение интерполяционного многочлена в этом случае означало бы повторение допущенных при измерениях ошибок.

В таком случае подбирается приближающая функция, график которой проходит не через заданные точки, а близко от них. В качестве такой функции

φ (x) выбираются различные элементарные функции(многочлен, степенная,

показательная, логарифмическая и	.др)	с неопределенными	параметрами
a0 , a1 ,...,am . Мерой отклонения φ (x)	от	заданной функции f (x)	на множе-

стве точек (xi , yi ) (i =1,..., n ) является величина S , равная сумме квадратов разностей между значениями табличной и аппроксимирующей функций в -за данных точках xi :

n

S = å[φ(xi ) - yi ]2 .

i=1

Параметры приближающей функции a0 , a1 ,..., am подбираются так, чтобы величина S была минимальной. В этом состоит метод наименьших квадратов. Чтобы найти минимум S = S (a0 , a1 ,...,am ), необходимо приравнять нулю все частные производные функции S :

17

¶S = 0, ¶S = 0, …, ¶S = 0 .

¶a0	¶a1	¶am
Полученные соотношения		составляют систему(m +1) уравнений с
(m +1) неизвестными. Из	системы	находим решение(единственое для боль-

шинства приближающих функций) – параметры a0 , a1 ,..., am , которые опреде-

ляют наилучшую аппроксимирующую функцию из рассмотренного класса функций. Такие функции называют эмпирическими.

Степень отклонения аппроксимирующей функции от табличной опреде-

ляется			числовым значением величиныS или приведенным отклонением
ε =		1	n éφ(x		)- y ù	2	, которое называется среднеквадратичным уклонени-
			åë	i	i û
		n i=1

ем. Сравнение среднеквадратичных уклонений среди всех наилучших в своем классе аппроксимирующих функций дает окончательный результат: функция, у которой ε наименьшее, есть оптимальное приближение.

Рассмотрим класс линейных функций φ (x) = a0 + a1 x , с помощью кото-

рых будем приближать табличную функцию f (x), заданной точками (xi , yi )

(i =1,..., n ). Методом наименьших квадратов найдем параметры a0							и a1 , кото-
рые определят	наилучшую					линейную зависимость. Рассмотрим	отклонение
n	- yi ]2 , которое необходимо минимизировать. Для этого запи-
S = å[a0 + a1xi
i=1
сываем систему уравнений:
			¶S			n
					= 2å[a0 + a1 xi - yi ] = 0 ;
			¶a0			i=1
		¶S				n
				= 2å[a0 + a1 xi - yi ]xi = 0.
		¶a1				i=1

Преобразуя уравнения, получаем:

n n

a0 × n + a1 × åxi = å yi ;

i=1 i=1

n

n

n

a0 × åx1 + a1 ×åxi2 = åxi yi .

i=1

= i 1

= i 1

Решая систему, находим a0 и a1 – параметры наилучшго приближения линейной функцией.

18

Пример. Задана табличная функция

	x	1	2	3	4		5
	y	4,8	2,5	1,4	0,8		0,3
Построить аппроксимирующую функцию в виде линейной зависимости
φ (x) = a0 + a1 x , методом наименьших квадратов						найтиa0 и a1 , вычислить

среднеквадратичное уклонение ε .

Решение. Для составления системы уравнений удобно расчеты сделать в виде следующей таблицы:

	xi		yi		x2			xi × yi
					i
	1	4,8		1			4,8
	2	2,5		4			5,0
	3	1,4		9			4,2
	4	0,8		16			3,2
	5	0,3		25			1,5
Сумма	15		9,8		55			18,7
Получаем систему уравнений:
			5a0 +15a1 = 9,8 ;
			15a0 + 55a1 =18,7 .
Отсюда	получаем a0 = 5,17				и	a1 = -1,07				и	зависимость

j(x) =5,17 -1,07x .

Рис. 5. Экспериментальные точки и график линейной эмпирической функции

19