18. Учет амплитуд и фаз вторичных волн позволяет в каждом конкретном случае найти амплитуду (интенсивность) результирующей волны в любой точке пространства, т. е. определить закономерности распространения света. В общем случае расчет интерфере­нции вторичных волн довольно сложный и громоздкий, однако, как будет показано ниже, для некоторых случаев нахождение амплитуды результирующего колебания осуществляется алгебраическим суммированием.

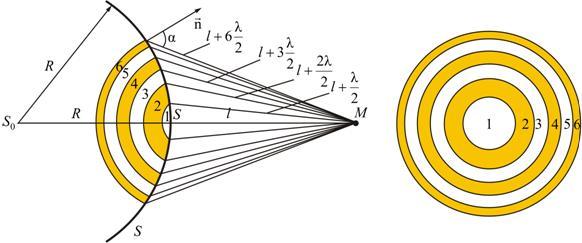
19.     Френель предложил оригинальный метод разбиения волновой поверхности S на зоны, позволивший сильно упростить решение задач (метод зон Френеля).

20.       Границей первой (центральной) зоны служат точки поверхности S, находящиеся на расстоянии 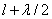  от точки M (рис. 9.2). Точки сферы S, находящиеся на расстояниях 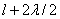 ,  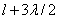, и т.д. от точки M, образуют 2, 3 и т.д. зоны Френеля.

21.       Колебания, возбуждаемые в точке M между двумя соседними зонами, противоположны по фазе, так как разность хода от этих зон до точки M     .

22. 

23. Рис. 9.2

24.       Поэтому при сложении этих колебаний, они должны взаимно ослаблять друг друга:

    ,

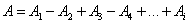    (9.2.2)

25.       где A – амплитуда результирующего колебания,   – амплитуда колебаний, возбуждаемая i-й зоной Френеля.

26.       Величина   зависит от площади 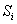  зоны и угла 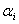  между нормалью к поверхности и прямой, направленной в точку M.

27.       Площадь одной зоны

28.  .

29.       Отсюда видно, что площадь зоны Френеля не зависит от номера зоны i. Это значит, что при не слишком больших i площади соседних зон одинаковы.

30.       В то же время с увеличением номера зоны возрастает угол 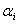  и, следовательно, уменьшается интенсивность излучения зоны в направлении точки M, т.е. уменьшается амплитуда  . Она уменьшается также из-за увеличения расстояния до точки M:

31.   .

32.       Общее число зон Френеля, умещающихся на части сферы, обращенной в сторону точки M, очень велико: при 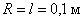 ,  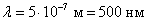, число зон 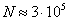 , а радиус первой зоны  .

33.       Отсюда следует, что углы между нормалью к зоне и направлением на точку M у соседних зон примерно равны, т.е. что амплитуды волн, приходящих в точку M от соседних зон, примерно равны.

34.       Световая волна распространяется прямолинейно. Фазы колебаний, возбуждаемые соседними зонами, отличаются на π. Поэтому в качестве допустимого приближения можно считать, что амплитуда колебания 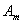  от некоторой m-й зоны равна среднему арифметическому от амплитуд примыкающих к ней зон, т.е.

35.  .

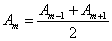36.       Тогда выражение (9.2.1) можно записать в виде

    .

    (9.2.2)

37.       Так как площади соседних зон одинаковы, то выражения в скобках равны нулю, значит результирующая амплитуда  .

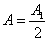38.       Интенсивность излучения    .

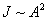39.       Таким образом, результирующая амплитуда, создаваемая в некоторой точке M всей сферической поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной, а интенсивность  .

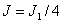40.       Так как радиус центральной зоны мал (  ), следовательно, можно считать, что свет от точки P до точки M распространяется прямолинейно.

41.       Если на пути волны поставить непрозрачный экран с отверстием, оставляющим открытой только центральную зону Френеля, то амплитуда в точке M будет равна 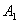 . Соответственно, интенсивность в точке M будет в 4 раза больше, чем при отсутствии экрана (т.к. 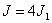 ). Интенсивность света увеличивается, если закрыть все четные зоны.

42.       Таким образом, принцип Гюйгенса–Френеля позволяет объяснить прямолинейное распространение света в однородной среде.

43.       Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально. Для этого используются зонные пластинки – система чередующихся прозрачных и непрозрачных колец.

44.       Опыт подтверждает, что с помощью зонных пластинок можно увеличить освещенность в точке М, подобно собирающей линзе.

46. Дифракция на круглом отверстии и диске.

37 Дифракция на круглом отверстии. Пусть R – радиус отверстия. Расчет удобнее вести в полярных координатах (r, ) и (r’, ’) в плоскостях отверстия и дифракционной картины:

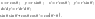(7.44)

Тогда (7.35) для этого случая запишется в виде:

(7.45)

где – функция Бесселя m-го порядка. Воспользуемся свойством функций Бесселя:

. (7.46)

Тогда получаем (рис.7.11):

. (7.47)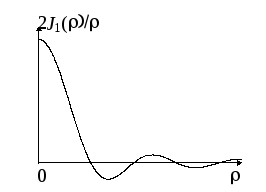

Интенсивность дифракционной картины определяется квадратом этой функции, т.е. в центре картины имеется светлое круглое пятно, окруженное темными и светлыми кольцами. Максимумы интенсивности быстро убывают. Радиусы колец определяются из корней функции Бесселя J₁ ()=0. Т.к. существует приближенное соотношение 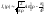, то качественно распределение интенсивности выглядит примерно так же, как и на рис.7.10. Угловой размер центрального светлого пятна (диска Эйри), наблюдаемого из центра круглого отверстия, равен:

47. .

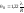48. Дифракция Френеля на диске:

49. Сферическая волна, распространяющаяся из точечного источника 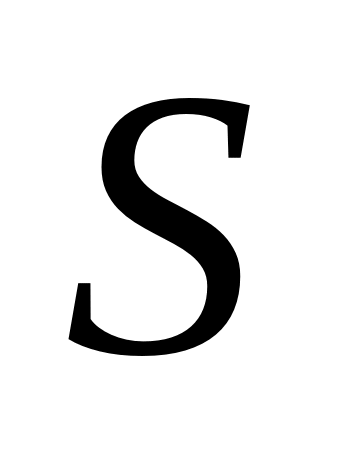, встречает на своем пути диск. Дифракционная картина наблюдается на экран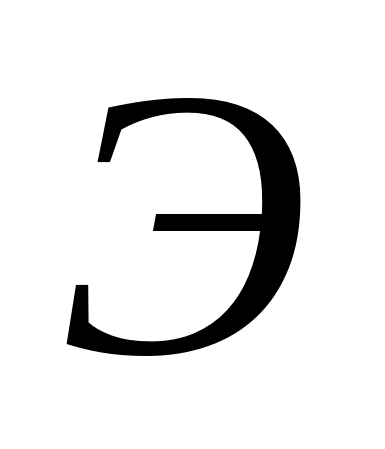е  в точке . Пусть диск закрывает  первых зон Френеля. Тогда амплитуда результирующего колебания в точке  равна:. Т.к. слагаемое в скобках равно 0, то . Следовательно, в точке 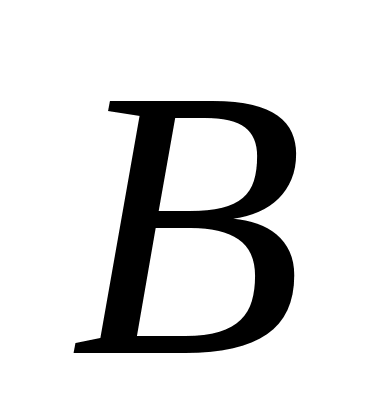 всегда будет светлое пятно, окруженное концентрическими светлыми и темными кольцами, а интенсивность убывает с расстоянием от центров картины.

51. Дифракция на одной щели.

Дифракция на щели.

Рассмотрим падение плоской монохроматической световой волны на бесконечную щель шириной b (рис.7.9). Участок dx, находящийся на расстоянии x от левого края щели (начала координат), в направлении Z’ излучает плоскую волну с запаздыванием фазы относительно точки О на kxЧsin. Угол отсчитывается от оси Z – нормали к щели (первоначального направления падающей волны), k – волновое число падающей волны. При записи амплитуды волны учтем, что вся щель в направлении = 0 посылает излучение с амплитудой E₀. Предполагая равномерное распределение амплитуды по щели, получим, что участок dx щели пошлет в направлении Z’ волну dE₁ с амплитудой E₀dx/b :

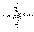
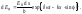(7.39)

Отсюда имеем для амплитуды волны от всей щели:

(7.40)

После несложного интегрирования и перехода от поля к интенсивности, получаем интенсивность дифракционной картины:

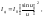(7.41)

где I₀ = E₀² ; I₁ = E₁² ; . (7.42)

Проанализируем выражение (7.41).

1. При = 0 u =0. Используя соотношение , получаем, что в центре дифракционной картины интенсивность максимальна и равна I₀ .

2. При углах , для которых sinu = 0, а u 0 интенсивность света обращается в нуль. Тогда условие минимума дифракционной картины на одиночной щели принимает вид:

(7.43)

3. Основная часть потока энергии сосредоточена в пределах изменения угла дифракции между первыми (n = 1) симметричными максимумами. График зависимости (7.41) приведен на рис.7.10.

4. Чем меньше (уже) щель, тем шире центральный максимум. Нетрудно заметить, что при b центральный максимум расплывается на всю полуплоскость ( /2). Дальнейшее уменьшение щели приводит лишь к монотонному уменьшению интенсивности прошедшего света.

Изучение картины дифракции дает информацию о ширине щели, если известна длина волны используемого света. Наоборот, зная ширину щели, можно найти длину волны. Таким образом, дифракционная картина от данного объекта имеет характерный вид, позволяющий получать информацию о размерах этого объекта. Отмеченное обстоятельство носит достаточно общий характер и лежит в основе метрологического применения дифракционных явлений.

Дифракционная решетка и ее применение.

Прозрачная (амплитудная) дифракционная решетка представляет собой правильную плоскую структуру из большого количества параллельных щелей с шириной каждой щели b и расстоянием d между соседними щелями. Расстояние d чаще называют периодом или постоянной дифракционной решетки (рис.7.12). Пусть на эту решетку нормально падает плоская монохроматическая волна. Найдем интенсивность света I в дифракционной картине.

Методика расчета и система обозначений та же, что и для одиночной щели. От элемента dx какой-то n-й щели в исследуемом направлении распространяется волна вида:

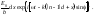(7.49)

Вся n-я щель пошлет волну вида:

(7.50)

Для учета действия всех щелей по принципу суперпозиции можно сложить все образовавшиеся напряженности поля:

(7.51)

где N – полное число щелей, участвующих в дифракции. Множитель с интегралом был посчитан выше для случая одной щели. Он не зависит от n и может быть вынесен за знак суммы. Введем обозначение:

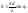(7.52)

Сумма в (7.51) представляет собой сумму N членов геометрической прогрессии. Тогда (7.51) перепишется в виде:

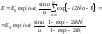(7.53)

Интенсивность света в дифракционной картине получается умножением (7.53) на комплексно сопряженную величину I=EE^* :

(7.54)

Множитель (sinu/u)² характеризует распределение интенсивности в результате дифракции плоской волны на каждой щели и является огибающей всей дифракционной картины, а множитель (sinN/sin)² учитывает интерференцию между волнами, исходящими от всех щелей. Множитель I₀ определяет интенсивность света, излучаемого в направлении = 0, которая зависит от потока энергии, падающего на решетку света. Вид дифракционной картины показан на рис.7.13.

Величина dsin равна разности хода между волнами, испускаемыми двумя эквивалентными точками соседних щелей. Условие главных максимумов для дифракционной решетки определяется формулой:

(7.55)

53. А условие (7.43) определяет положение минимумов огибающей.

Рассеяние света. Дифракция на пространственной решетке, Условие Вульфа-Бреггов.

Пространственной, или трехмерной, дифракционной решеткой называется такая оптически неоднородная среда, в которой неоднородности периодически повторяются при изменении всех трех пространственных координат.

      Условия прохождения света через обычную дифракционную решетку периодически изменяются только в одном направлении, перпендикулярном к оси щели. Поэтому такую решетку называют одномерной.

      Простейшую двумерную решетку можно получить, сложив две одномерные решетки так, чтобы их щели были взаимно перпендикулярны. Главные максимумыдвумерной решетки должны одновременно удовлетворять условию максимума для каждой из решеток:

      и      ,

      где φ  - угол между направлением на главный максимум (направление луча) и нормалью к решетке;  m – порядок дифракционного максимума.

      Дифракционная картина представляет собой систему светлых пятен, расположенных в определенном порядке на плоскости экрана. Размеры этих пятен уменьшаются при увеличении числа щелей, а яркость возрастает. Такая же картина получается, если на одно стекло нанести ряд взаимно перпендикулярных полос.

      Дифракция наблюдается также и на трехмерных структурах. Всякий монокристалл состоит из упорядоченно расположенных атомов (ионов), образующих пространственную трехмерную решетку (естественная пространственная решетка).

      Период атомной решетки порядка  ; длина волны света  . При таких условиях никаких дифракционных явлений на атомных дифракционных решетках с видимым светом не будет. Нужно излучение с меньшей длиной волны, например рентгеновское. Для рентгеновских лучей кристаллы твердых тел являются идеальными дифракционными решетками.

      В 1913 г. русский физик Г.В. Вульф и английские ученые отец и сын Генри и Лоуренс Брэгги, независимо друг от друга, предложили простой метод расчета дифракции рентгеновских лучей в кристаллах. Они полагали, что дифракцию рентгеновских лучей можно рассматривать как результат отражения рентгеновских лучей от плоскостей кристалла. Это отражение, в отличие от обычного, происходит лишь при таких условиях падения лучей на кристалл, которые соответствуют максимуму интерференции для лучей, отраженных от разных плоскостей.

      Направим пучок рентгеновских лучей 1 и 2 на две соседние плоскости кристалла   и  (рис. 9.9).

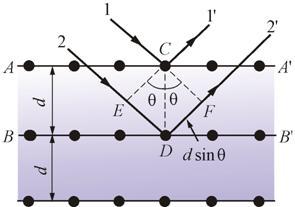
Рис. 9.9

      Абсолютный показатель преломления всех веществ для рентгеновских лучей равен 1. Поэтому оптическая разность хода между лучами   и 

 ,

      где θ – угол между падающими и отраженными лучами и плоскостью кристалла (угол скольжения).

      Интерференционные максимумы должны удовлетворять условию Вульфа–Брэггов:

,   (m = 1, 2, 3, ... .).

(9.5.1)

      Из формулы (9.5.1) видно, что дифракция будет наблюдаться лишь при    . Т. е. при условии   будут отсутствовать дифракционные максимумы. Поэтому условие   называют условием оптической однородности кристалла.

      Из (9.5.1) следует, что наблюдение дифракционных максимумов возможно только при определенных соотношениях между λ и θ. Этот результат лежит в основеспектрального анализа рентгеновского излучения, так как длину волны определяют по известным d, m и измеренному на опыте углу.

      Исследуя дифракцию рентгеновских лучей, можно решить и обратную задачу: если известна длина волны λ рентгеновских лучей, можно определить период кристаллической решетки d и ориентацию атомных плоскостей в пространстве. Эта идея была высказана немецким физиком М. Лауэ в 1912 г. и явилась существенным вкладом в развитие физики твердого тела.

      Поликристаллические образцы представляют собой множество мелких кристалликов, ориентированных хаотически в пространстве. Направим на кристалл монохроматический пучок рентгеновских лучей с известной длиной волны λ, и всегда найдутся кристаллы, ориентированные под нужным углом, а рефлексы (светлые точки на фотопластинке) от разных кристаллов образуют концентрические окружности D₁, D₂, D₃ (рис. 9.10).

Рис. 9.10

      При облучении монохроматическим рентгеновским излучением от источника S поликристаллического образца O c беспорядочной ориентацией кристаллических плоскостей для различных направлений возникают конусы направлений D₁, D₂, D₃,…, в которых выполнено условие Вульфа-Брэггов. Этот метод был предложен в 1926 г. П. Дебаем и П. Шеррером (метод Дебая–Шеррера).

Рис. 9.11

      На рис. 9.11 показана дебаеграмма в методе рентгеноструктурного анализа Дебая–Шеррера.