3.1.3 Интервальная характеристика

При повторных измерениях одного и того же размера могут быть получены различные значения. Это объясняется действием случайных погрешностей. Это действие оценивается вероятностным разбросом результатов многократных измерений в виде доверительного интервала.

Доверительный интервал представляет собой интервал значений, в пределы которого входит измеренный размер с доверительной вероятностью. Доверительный интервал определяется по формуле:

, (3.23)

где n  число измерений;

 среднее арифметическое значение результата измерений;

S  СКО результата измерений:

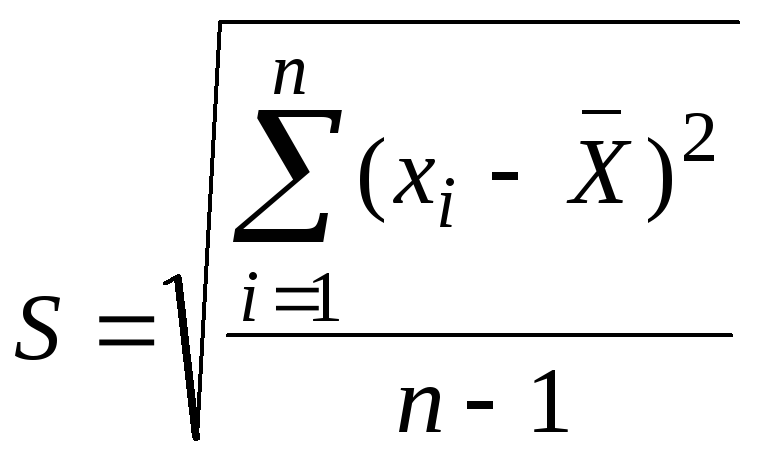(3.24)

t_p – коэффициент Стьюдента для доверительной вероятности Р.

Значение доверительной вероятности задается до начала измерений и обычно равно 0,95. Другие её значения специально оговариваются.

3.2 Вопросы для самопроверки

1. Почему результаты измерений рассматриваются как случайные величины?

2. Какая величина является случайной?

3. Что такое массовое событие?

4. Что называется дискретной случайной величиной?

5. Какие случайные величины называются аналоговыми?

6. Какими вероятностными характеристиками можно описать случайную величину?

7. Как определить абсолютную частоту?

8. Что характеризует относительная частота?

9. Как определить функцию распределения вероятностей для случайной величины: а) дискретной; б) аналоговой?

10. Изобразите графически распределения вероятностей, плотности вероятности, функцию накопленных относительных частот и функцию распределения вероятностей.

11. Что определяет функция распределения вероятностей?

12. Как определить вероятность попадания случайной величины в заданный интервал на основании известной6 а) функции распределения вероятностей; б) плотности распределения вероятностей?

13. Почему для описания случайной величины чаще используются числовые характеристики?

14. Как определяются: а) начальные моменты; б) центральные моменты?

15. Как называется, как определяется и что характеризует первый начальный момент?

16. Какие центральные моменты используются для характеристик случайных величин?

17. Какими характеристиками определяется разброс случайных величин?

18. Определите степень размерности, которую могут иметь: а) дисперсия; б) СКО.

19. Приведите формулы для расчета дисперсии: а) если для каждого результата измерений задана абсолютная частота; б) если значения результатов измерений не повторяются; в) с использованием математического ожидания; в) с использованием вероятностей получения каждого результата.

20. Что характеризует и как определяется асимметрия?

21. Что такое эксцесс, и через какой момент определяется его значение?

22. Что определяют для случайной величины: а) статистическая мода; б) статистическая медиана?

23. Что называется доверительным интервалом?

24. Почему результат многократных измерений представляют в форме доверительного интервала?

25. Что такое доверительная вероятность?

3.3 Примеры решения задач

Задача 3.3.1. Произведены измерения выходного напряжения в выборке из партии микросхем. Результаты измерений представлены в таблице 3.1.

Таблица 3.1  Результаты измерений напряжения

Интервалы значе-ний напряжения U, мВ	210-212	212-214	214-216	216-218	218-220	220-222	222-224
Число значений mί	5	12	28	75	52	20	8

Определите характеристики результата измерений выходного напряжения:

а) вероятностные  в виде гистограммы и функции накопленных частот;

б) числовые  в виде среднего арифметического значения и СКО;

в) интервальную  в виде доверительного интервала.

Решение.

а) Число значений в каждом интервале m_ί является абсолютной частотой. Рассчитываем относительные частоты для каждого интервала:

P_ί=, (3.25)

где n  общее число результатов измерений:

, (3.26)

где r  число интервалов, r = 7.

n = 5+12+28+75+52+20+8=200

Р₁ = ; Р₂ = ; Р₃ =; Р₄ = ;

Р₅ = ; Р₆ =; Р₇ =.

Определяем ширину интервала:

(3.27)

где U_max и U _min  наибольшее и наименьшее значения напряжения.

(мВ)

Рассчитываем аналог плотности вероятности:

(3.28)

; ;;

; ;.

Строим гистограмму, отложив по оси ординат величины Р_ί, как показано на рисунке 3.6, а.

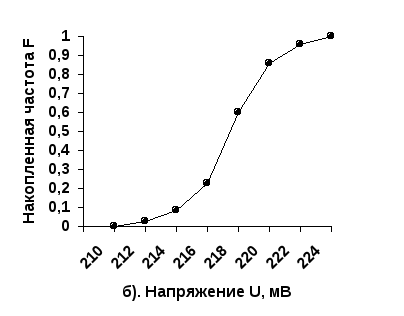
Рассчитываем накопленные относительные частоты F_ί для каждого интервала:

(3.29)

F₁=P₁=0,025;

F₂=P₁+P₂=0,025+0,06=0,085;

F₃=P₁+P₂+P₃=0,025+0,06+0,14=0,225;

F₄=P₁+P₂+P₃+P₄=0,025+0,06+0,14+0,375=0,6;

F₅=P₁+P₂+P₃+P₄+P₅=0,025+0,06+0,14+0,375+0,26=0,86;

F₆=P₁+P₂+P₃+P₄+P₅+P₆=0,025+0,06+0,14+0,375+0,26+0,1=0,96;

F₇=P₁+P₂+P₃+P₄+P₅+P₆+P₇=0,025+0,06+0,14+0,375+0,26+0,14+0,04=1;

б) Для расчета числовых характеристик определим середину каждого интервала:

(3.30)

где х_Hi ,x_Bi – нижняя и верхняя границы i-го интервала.

х₁ = 211мВ; х ₂= 213мВ; х₃ = 215мВ; х ₄= 217мВ; х₅ = 219мВ; х ₆= 221мВ; х₇ = 223мВ.

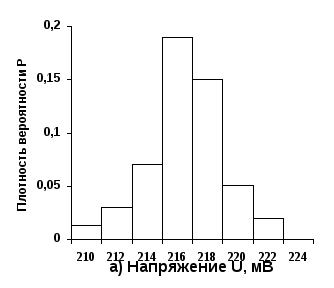
Рисунок 3.6 Гистограмма (а) и функция накопленных относительных частот (б)

Среднее арифметическое значение определяем по формуле (3.11):

(211∙5+213∙12+215∙28+217∙75+219∙52+221∙20+223∙8)=217,49 (мВ)

СКО рассчитываем по формуле (3.16). Для небольшого числа данных СКО генеральной совокупности σ(х) заменяем на выборочное СКО S.

=2,508257719 (мВ)

в) Рассчитываем доверительный интервал по формуле (3.23). Так как значение доверительной вероятности не задано, то принимаем Р=0,95 по приложению А определяем значение коэффициента Стьюдента t_p=1,96.

Доверительный интервал:

217,49-1,96

Задача 3.3.2. Производится стрельба по цели до первого попадания. Вероятность попадания Р_n при каждом выстреле равна 0,6. На стрельбу отпущено 4 снаряда. Вычислить для числа израсходованных снарядов: математическое ожидание, дисперсию и СКО.

Решение.

Число израсходованных снарядов х может принимать значения: х₁=1, х₂=2, х₃=3, х₄=4.Определим вероятности этих значений.

Вероятность попадания 0,6, тогда вероятность промаха Р_н =1-0,6=0,4. Если на стрельбу потребовался только 1 снаряд, то значит попали в цель с 1-го раза, т.е. Р₁=0,6. При необходимости в двух снарядах – первым не попали, а поразили цель вторым. Т.е. для х₂=2:

Р₂=Р_n∙Р_н (3.31)

Р₂=0,6∙0,4=0,24

Для х₃=3:

Р₃=Р_н∙Р_н∙Р_n=Р_н²∙Р_n (3.32)

Р₃=0,4∙0,4∙0,6=0,096;

Для х₄=4 вероятность определяется двумя ситуациями: либо не попали всеми четырьмя снарядами, либо попали последним снарядом:

Р₄=Р_н⁴+Р_н ³Р_n; (3.33)

Р₄=0,4⁴+0,4³∙0,6=0,4³ (0,4+0,6)=0,4³=0,064.

Математическое ожидание:

(3.33)

М(х)=1∙0,6+2∙0,24+3∙0,096+4∙0,064=1,624≈1,6 (снаряда)

Дисперсия:

(3.34)

D(x)=(1-1,6) ²∙0,6+(2-1,6)²∙0,24+(3-1,6) ²∙0,096+(4-1,6) ²∙0,064=0,8112 (снаряда²);

СКО: σ(х)= (3.35)

σ(х)= (снаряда)

Задача 3.3.3. Средний процент выпуска брака на предприятии 1,2%.СКО брака σ(х)=0,15%. Определите вероятность того, что в отдельные дни процент брака будет находиться в пределах от 0,8% до 1,4%. Предполагается, что величина подчиняется нормальному закону распределения.

Решение.

Соответствие нормальному закону распределения позволяет для определения вероятности измеряемой величины воспользоваться функцией Лапласа (приложение Б).

Определим для каждой границы интервала значение квантили:

; (3.36)

где х_н  нижняя граница интервала;

х_в  верхняя граница интервала.

;

По приложению Б определяем значения функции Лапласа для найденных значений квантилей:

Ф(t_Н)=Ф(2,67)=0,4962; Ф(t_В)=Ф(1,33)=0,4082.

Рассчитываем вероятность попадания величины в интервал [t_н ; t_в] :

Р=Ф(t_Н)+Ф(t_В) ( 3,37)

Р=0,4962+0,4082=0,9044

Задача 3.3.4. Определите минимальный объем выборки n, чтобы с надежностью 0,96 точность оценки математического ожидания измеренного параметра партии с помощью выборочного среднего равна 1,2 мм, если СКО σ равно 0,8 мм.

Решение.

Исходя из формулы (3.23) отклонение от математического ожидания оценивается доверительной погрешностью:

ε=(3.38)

Тогда (3.39)

σ=0,8 мм; ε=1,2 мм.

Коэффициент Стьюдента можно определить по приложению Б:

Ф(t_p)= (3.40)

Ф(t_p)=; t_p=2,055.

Объем выборки: n= (шт.)