GPSS / Simulation

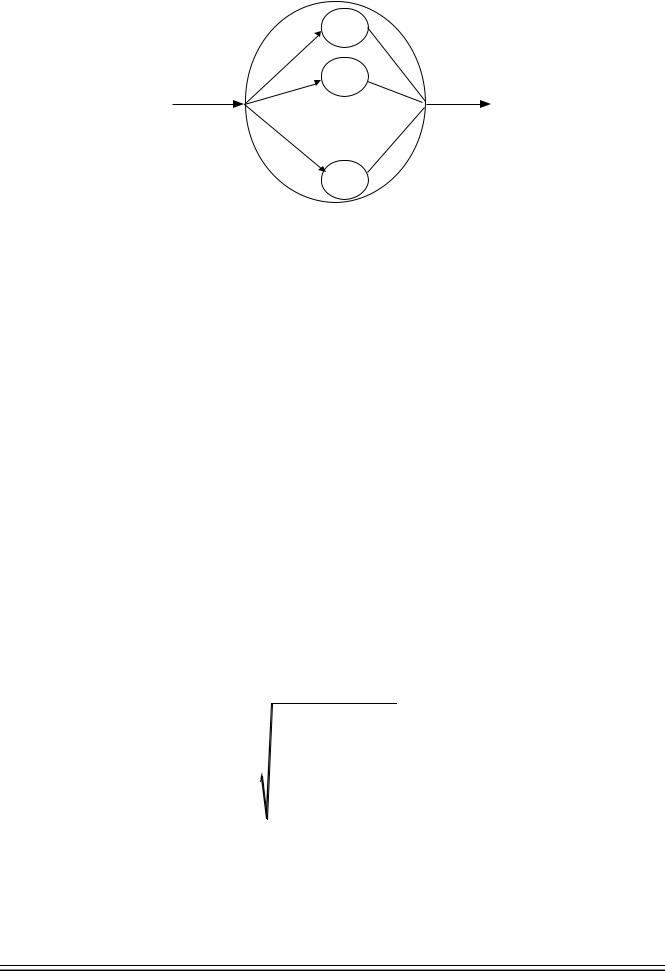
Е.В.Малахов. Имитационное моделирование. Конспект лекций.	11

1

P1

2

P2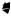

Pk

k

Рис. 11. Генератор потока заявок с гиперэкспоненциальным распределением.

Pi — вероятность попадания заявки в i-ый элементарный блок. В n-канальном приборе следующая заявка поступает, когда освобождается канал. Здесь, как и в случае с последовательным соединением, заявка не принимается, пока предыдущая не покинет устройство в целом. На выходе такого генератора мы получим поток, характеризующийся следующей плотностью распределения:

k

f t Pi i e it ,

(10)

i 1

k

где Pi

1 ,

Pi

0 .

i 1

Распределение с такой плотностью называют гиперэкспоненциальным, его

математическое ожидание и дисперсия равны

k

P

k

P 2

2

i

D 2

i

(11)

i 1

i

i 1 i

k

Pi

E

(12)

i

i 1

Соответственно, его коэффициент вариации определяется выражением

k

2

Pi

2

i 1

i

1

(13)

k

P

2

i

i 1 i

Характерной особенностью всех этих потоков является то, что для

гиперэкспоненциального потока коэффициент вариации H 1,

для простейшего потока s =1,

для потока Эрланга 0 < E 1.

И, наконец, если для потока Эрланга

k ,

то lim k

0 ,

и в результате получаем

k

регулярный поток с T const.

Кафедра математического обеспечения компьютерных систем. ОНУ им. И.И. Мечникова.

Е.В.Малахов. Имитационное моделирование. Конспект лекций.	12

Марковские процессы

Эти процессы характеризуют такие системы, состояние которых в момент t0 не зависит от того, когда и при каких обстоятельствах система перешла в это состояние, а зависит от состояния системы в предыдущий момент времени t t0 .

Существует два вида марковских процессов:

1.с дискретным временем, в которых изменение состояния в моменты, определяется целыми числами (тактами);

2.с непрерывным временем, изменение состояния которых может произойти в любой момент времени. В этом случае длительность пребывания системы в каком-либо состоянии является случайной величиной.

	Марковские процессы можно задавать следующими способами:
1.	С помощью графа, напоминающего диаграммы переходов
	конечных автоматов:	Si	Sj
2.	С помощью матриц вероятностей переходов:

	p11	p12	p13	p1n	n	Sk	S
							l
pij					, где pij	1 .
	pn1			pnn	j 1	Рис. 12. Марковский процесс.

При моделировании систем нас будут интересовать такие важные характеристики как вероятность пребывания системы в состоянии r в произвольный момент времени k: Pr(k).

Марковские процессы с дискретным временем

Рассмотрим расчет упомянутых характеристик на примере марковского

процесса с дискретным временем: задано

описание марковского процесса, требуется

определить вероятности состояний через k

шагов развития этого процесса.

1. k = 0, пусть в 0-й момент времени система находится в j-м состоянии Pj(0) = 1, Pi(0) = 0, i j ;

2.k = 1, вероятность пребывания в r-м

состоянии зависит от вероятности перехода в это состояние из j-го:

P1 1 Pj1 , , Pn 1 Pjn

k = 0	k = 1	k = 2
S1	S1	S1

		Pr1
Pjr	Sr	Prr	Sr …
Sj
Pjn		Prn
Sn	Sn		Sn

Рис. 13. Развитие дискретного марковского процесса.

Кафедра математического обеспечения компьютерных систем. ОНУ им. И.И. Мечникова.

Е.В.Малахов. Имитационное моделирование. Конспект лекций.	13

3.k = 2, пребывание системы в r-м состоянии на этом шаге зависит от вероятности перехода в него при условии, что на шаге k = 1 система находилась в одном из n состояний. Т.е., имеем условную вероятность. Т.к. события, переводящие систему в новое состояние, независимы,

она будет равна сумме произведений вероятностей пребывания в исходных состояниях и вероятностей переходов в новое:

P1 2 P1 1 P11 P2 1 P21 Pn 1 Pn1

n

Pr 2 P1 1 P1r P2 1 P2r Pn 1 Pnr Pj 1 Pjr

j 1

На произвольном шаге k вероятность пребывания системы в r-м состоянии:

n	k 1 Pjr , где r 1, n
Pr k Pj		(14)

j 1

Пример. Пусть система (например, компьютер) может находиться в одном из четырех состояний: S1 — исправна; S2 — частично неисправна (неисправность не мешает решению основных задач (например, отказал один из дисководов)); S3 — тяжелая неисправность (система может решать ограниченное число задач (например, отказ жесткого диска и большей части микросхем оперативной памяти)); S4 — неисправна (например, вышел из строя микропроцессор).

Матрица вероятностей переходов имеет следующий вид:

	0.3 0.4		0.1 0.2
P	0	0.2	0.5	0.3	, соответственно, граф:
ij	0	0	0.4	0.6
	0	0	0	1
	Определим вероятности того или иного уровня

функционирования системы в первые			два момента
времени:
1) k = 0;	P1 0 1 ; P2 0 P3 0 P4 0 0
2) k = 1;	P1 1 0.3 ;	P2 1 0.4 ;	P3 1 0.1 ;
P4 1 0.2

			0.3
		1
	0.4		0.1	0.2
2	0.5	3	0.6	4
0.2			0.4
	0.3

Рис. 14. "Жизненный цикл" вычислительной системы.

3) k = 2; P1 2 P1 1 P11

P2 2 P1 1 P12 P2 1 P22

P3 2 P1 1 P13 P2 1 P23 P3 1 P33

P4 2 P1 1 P14 P2 1 P24 P3 1 P34 P4 1 P44

Аппарат дискретных марковских процессов применяется, например, для оценки

Кафедра математического обеспечения компьютерных систем. ОНУ им. И.И. Мечникова.

Е.В.Малахов. Имитационное моделирование. Конспект лекций.	14

эффективности алгоритмов или вычисления трудоемкости алгоритмов.

Марковские процессы с непрерывным временем

Пусть Pi(t), где i 1, n — вероятность пребывания системы в i-ом состоянии, Pij —

вероятность перехода из i-го в j-ое состояние. Но, т.к. такой переход может произойти в любой момент времени, мы можем рассматривать вероятность того, что система перейдет из i-го в j-ое

состояние за интервал t:

Pij ( t )

и при t 0 в пределе получим величину

lim

Pij t

—

t

t 0

t

ij

интенсивность перехода или плотность вероятности перехода.

С некоторым приближением можно считать, что Pij t ij

t .

Для получения вероятностей пребывания системы в каком-

12

1

31

либо состоянии рассмотрим следующий пример:

23

Вероятность того, что система находится в состоянии S1

в

2

3

32

течение интервала t,t t ,

определяется из следующих

Рис. 15. Марковский процесс с

соображений:

непрерывным временем.

1)предположим, что система в момент времени t находилась в S1 и за интервал времени t не изменила его. Вероятность этого события равна P1 t 1 P12 t P1 t 1 t 12

2)однако в момент времени t система могла находиться в состоянии S3 и за интервал t

перейти в S1. Вероятность этого факта равна P3 t t 31 .

Учитывая уравнения расчета вероятностей пребывания системы в j-м состоянии, можно записать:

P1 t t P1 t 1 t 12 P3 t t 31 .

Отсюда

P1 t t P1

t

12P1 t P3 t 31

t

Перейдя к

lim , получим

t 0

dP1 t

12 P1

t 31 P3 t

dt

Аналогично , запишем для 2 и 3 состояний

:

dP2 t

(15)

12

P t

23

P

t

32

P

t

dt

1

2

3

dP3 t

23 P2 t

31 32 P3 t

dt

Данная система уравнений носит название уравнений Колмогорова–Чепмена.

Кафедра математического обеспечения компьютерных систем. ОНУ им. И.И. Мечникова.

Е.В.Малахов. Имитационное моделирование. Конспект лекций.	15

Из данного простого примера можно вывести правила составления этих уравнений:

1.В левой части записывается производная вероятности исследуемого состояния марковского процесса.

2.В правой части — сумма, включающая столько членов, сколько дуг связано с исследуемым состоянием (т.е. равно степени вершины графа).

2.1.Каждый член правой части представляет собой произведение плотности вероятности перехода, соответствующей данной дуге, на вероятность состояния, из которого дуга выходит.

2.2.Если дуга выходит из исследуемого состояния, то соответствующий член сопровождается знаком /-/, если дуга входит в это состояние — то соответствующий

знак /+/.

Если марковский процесс

a)имеет конечное число состояний,

b)из каждого состояния существует путь в любое другое состояние1,

то можно доказать, что распределение вероятностей пребывания системы в j-ых состояниях —

Pj(t) (для непрерывного процесса) и Pj(k) (для дискретного процесса) — сводится к некоторому

стационарному распределению {Pj}, которое, в свою очередь, не зависит от начального

состояния.
	Это свойство называется эргодичностью системы.
	На практике это означает следующее: для систем с непрерывным временем предел
вероятности				j-го состояния при t равен некоторой постоянной величине:
lim P	j	t P	j	const 2.
t

Вэтом случае система дифференциальных уравнений Колмогорова-Чепмена вырождается

всистему алгебраических уравнений. Для приведенного выше примера это выглядит следующим образом:

	P				P 0
		12	1	31		3
		P		P			P 0	, с нормирующим условием		P		1	(16)
											j
		12 1	23	2		32	3
			31 32 P3 0						j
	23 P2

Величину ijPi называют потоком вероятности перехода из i в j.

1Т.е. возможен переход в любое другое состояние, даже через некоторую последовательность промежуточных состояний.

2Хотя система в стационарном режиме меняет свои состояния случайным образом, их вероятности уже не зависят от времени. Каждая такая вероятность Pj характеризует относительное время или долю времени пребывания системы в данном (j-м) состоянии.

Кафедра математического обеспечения компьютерных систем. ОНУ им. И.И. Мечникова.

Е.В.Малахов. Имитационное моделирование. Конспект лекций.	16

Для дискретной системы стационарные вероятности рассчитываются по аналогичной системе уравнений, где вместо положительной или отрицательной интенсивностей

вероятностей фигурируют вероятности переходов.

Справедливость этого факта для дискретной системы можно проверить на следующем

примере:
Задав	конкретные				величины Pij, можно рассчитать			P11
стационарные вероятности Pj по следующей системе:						P12	1	P31
P P P				P P			P
	1	1	11	3	31		32
P2		P1	P21	P3	P32	2		3
		P2	P23				P23
P3
P		P	P	1
	1	2	3			Рис. 16. Марковский процесс
Если затем рассчитать вероятности состояний Pj(k), то можно						с дискретным временем

убедиться, что уже при k = 4 5 вероятности Pj(k) будут приблизительно равны Pj, независимо от того, какое из состояний считать начальным.

Алгоритм расчета марковской цепи

Итак, для моделирования системы с помощью марковских процессов необходимо:

1.Задать потоки событий. Принятое обозначение: — интенсивность потока поступления заявок, — потока обслуживания.

2.Определить состояния марковского процесса (перечислить или задать функцию,

генерирующую все состояния).

3.Получить размеченный граф марковского процесса.

4.Составить и решить уравнения Колмогорова для стационарных состояний Pj.

5.Рассчитать характеристики модели: w — время ожидания заявок в очереди, l — длину очереди, u — время пребывания заявок в системе, n — среднее количество заявок в системе.

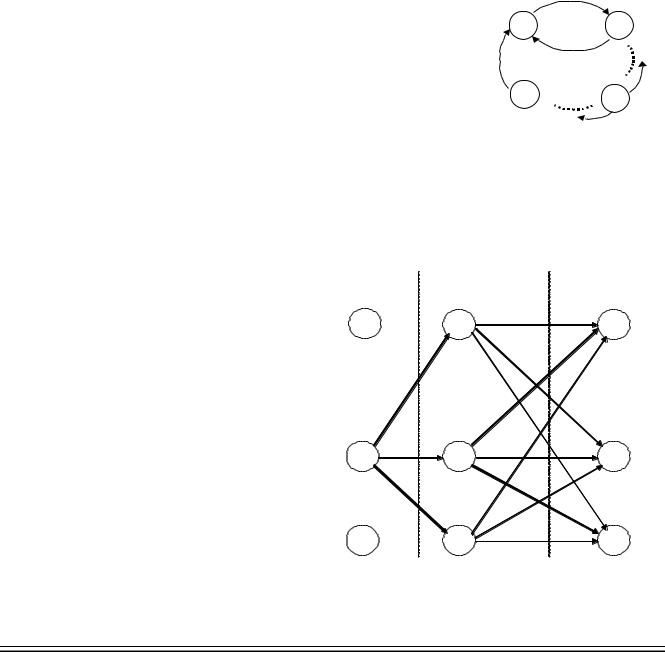
Системы локального баланса

Предположим, что система может менять				k
состояние последовательно. Марковский процесс					(i)		(i+1)
удовлетворяет условиям локального баланса,				i-1	i	i+1
если для любой пары его состояний существуют					(i+1)		(i+2)
переходы	в обоих	направлениях либо		j-1
отсутствуют вообще:
Можно доказать, что для таких марковских
процессов	вероятности	перехода соседних		Рис. 17. Система локального баланса.

Кафедра математического обеспечения компьютерных систем. ОНУ им. И.И. Мечникова.

Е.В.Малахов. Имитационное моделирование. Конспект лекций.									17
состояний равны: i Pi i 1 Pi 1 .
Вот абстрактный простейший пример подобной системы.
В систему поступают заявки	с	интенсивностью	,
принимаются на обслуживание	и	обслуживаются	с	0	1		2
интенсивностью .
				Рис.	18. Простейшая марковская цепь.

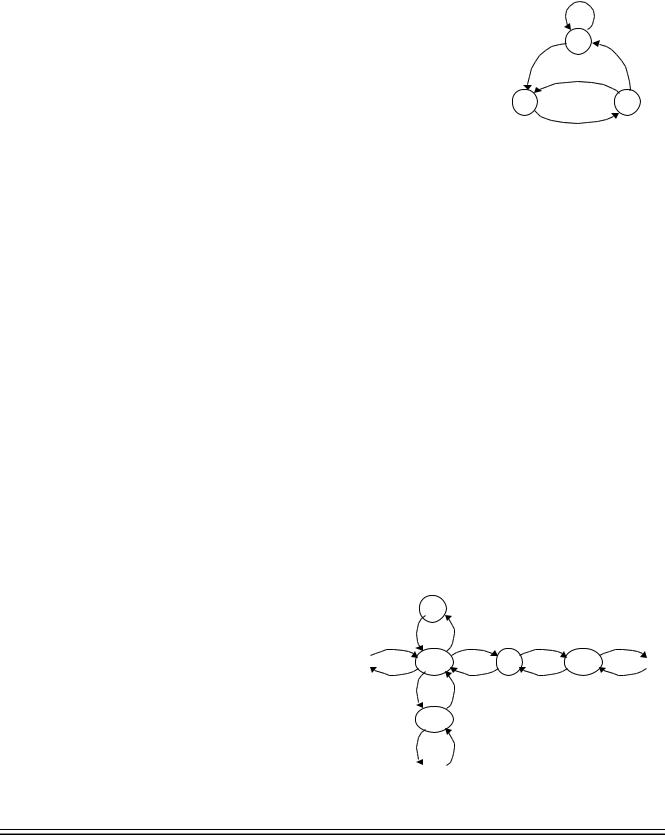
Состояния системы определяются количеством заявок

в ней: S0 — заявок в системе нет; S1 — в систему поступила одна заявка и была принята на обслуживание; S2 — в системе две заявки (одна — на обслуживании и одна — в очереди) и т.д.

Каждый переход в следующее (старшее) состояние осуществляется с интенсивностью .

Затем одна заявка обслужена и ушла из системы. Соответственно, заявок в системе стало на 1 меньше, а это — предыдущее (младшее) состояние марковской цепи. Такой переход осуществляется с интенсивностью .

Аналогичными графами представляются биологические процессы изменения популяции животных. Поэтому такие марковские процессы называют еще процессами размножения и гибели.

Кафедра математического обеспечения компьютерных систем. ОНУ им. И.И. Мечникова.

		Е.В.Малахов. Имитационное моделирование. Конспект лекций.					18
		Системы массового обслуживания
Теперь рассмотрим моделирование СМО с использованием аппарата марковских
процессов. Отметим еще раз их параметры и характеристики.
Параметры:						О
							ОП
1	— интенсивность потока заявок (характеризуется
a						w	b
	коэффициентом вариации a);
						u
1	—	интенсивность	обслуживания	заявок	Рис. 19. Параметры и характеристики
b
	(характеризуется коэффициентом вариации b);					СМО.
N	— количество каналов обслуживающих приборов.
Характеристики:
t		— среднее время ожидания обслуживания (пребывания в очереди);
u b		— среднее время пребывания заявок в системе;
l		— средняя длина очереди, что фактически соответствует вероятности P l i того,
		что система находится в i-ом состоянии
n		— среднее число заявок в системе в целом
Башарин и Кендал ввели следующую мнемонику для описания СМО: A/B/C, где
A — тип входного потока заявок,
B — тип потока обслуживания,
C — канальность прибора.
При этом C может принимать значения 1, N или .
Параметры A и B могут принимать одно из следующих обозначений:
M — простейший поток событий (показательное распределение) = 1
Ek — поток Эрланга k-го порядка 1
			k
D — детерминированный или регулярный поток = 0. В этом случае время поступления или
время обслуживания заявок постоянно, a или b соответственно равно const.
G — поток общего вида (генеральное распределение) 0
Hk — гиперэкспоненциальное распределение k-го порядка.
Соответственно, СМО M/G/1 означает, что в СМО поступает простейший поток событий
(ППС), заявки обслуживаются произвольно на одноканальном приборе. Аналогично, G/G/N —
это предельно общий случай СМО.

Кафедра математического обеспечения компьютерных систем. ОНУ им. И.И. Мечникова.

Е.В.Малахов. Имитационное моделирование. Конспект лекций.	19

Система М/М/1

В соответствии с обозначением на вход поступает ППС, время обслуживания имеет показательное распределение, количество каналов в приборе — 1.

Исследование СМО будем проводить, согласно алгоритму анализа марковских цепей.

1.Интенсивность входного потока — ,

интенсивность обслуживания — .

2.Состояние системы будет связанно только с количеством заявок:

S0 — нет заявок,

S1 — в системе одна заявка на обслуживании,

S2 — в системе две заявки: одна — на обслуживании, одна — в очереди,

…

Si — в системе i заявок: одна — на обслуживании, i-1 — в очереди.

3.Если нет ограничений на длину очереди, то число состояний такой системы бесконечно.

Т.к. простейший поток событий не обладает последействием, то все i .

Аналогично, i .

Получаем размеченный граф марковского процесса:

0	1	2			i

Рис. 20. Граф марковского процесса СМО M/M/1.

4. Составляем уравнения Колмогорова-Чепмена Система обладает свойством эргодичности, поэтому можно записать систему

алгебраических уравнений.

P0 P1 0
P P P 0
	0	1	2
		P P
P				0
	i 1	i	i 1

P P				P1 P0
	0	1		P 2 P
P P
	1	2			2	0
		Pi 1			P	i
Pi						P
					i	0

Величину называют вероятностью загрузки прибора или просто загрузкой

прибора. Т.к. 1 b , то b — среднее время обслуживания одной заявки.

Интерпретация загрузки следующая.

Возьмем интервал времени T. За это время в систему поступит T заявок. Время

	обслуживания этих заявок — T b. Переходя к пределу при T , получим lim	T b	b . Т.е.
		T
	T

Кафедра математического обеспечения компьютерных систем. ОНУ им. И.И. Мечникова.

Е.В.Малахов. Имитационное моделирование. Конспект лекций.	20

загрузка — это среднее число требований, которые поступят в систему за среднее время обслуживания одной заявки.

С другой стороны, — это вероятность того, что обслуживающий прибор занят в

произвольный момент времени (в момент поступления следующего требования). Эта вероятность характеризует среднее число заявок, находящихся на обслуживании в этот произвольный момент времени.

Соответственно, вероятность (коэффициент) простоя прибора: 1 .

Теперь можно записать уравнение для вероятности любого состояния в следующем общем

виде:

Pi i P0 , где i=1, 2, …

при нормирующем условии Pi 1 .

i 0

Подставляя в эту сумму выражение (17), получим:

P0 1 i 1

Откуда:

		P 1 i 1
		0
При 1 обеспечивается сходимость ряда (суммы)
равен	1	, и существование стационарных вероятностей.
	1

(17)

(18)

S 1 i , который

Подставляя полученное значение S в выражение для P0, получим: P0 1 , при < 1.

Используя (17), получим:

P0	1
P	1
1		(19)

Pi i 1

5. Используя систему (19), можно охарактеризовать количество заявок n в системе в соответствии с геометрическим законом распределения числа заявок в СМО M/M/1.

n M i iPi	i i 1 1 i i		(20)
i 0	i 0	i 0

Рассмотрим бесконечный ряд S 1 i i и распишем его подробнее:

i 0

Кафедра математического обеспечения компьютерных систем. ОНУ им. И.И. Мечникова.