GPSS / Simulation

Е.В.Малахов. Имитационное моделирование. Конспект лекций.	21

S	1	2 2			3 3		4 4					2 2 3 3 3 4
разобъем			на
частичные				2							2 3 4 3 4
	суммы
						3		4
ести выделим частичные суммы,
	то увидим, что с таким рядом															2				3					2		3		4
уже сталкивали сь, следовател ьно
								1						1					1							1
	в числителе - опять					1
первая частичная сумма
						1							1		2
					в выражение для n, получим: n
Подставив S1																								.								(21)
																						1

Сдругой стороны, n l , где — число заявок на обслуживании, l — число заявок

вочереди. Откуда:

l n			2
				— среднее количество заявок в очереди.
	1		1

Если w — среднее время ожидания заявок в очереди, то l w w l .

Это выражение носит название формулы Литтла.

Мы уже отмечали, что полное время пребывания заявок в СМО:

u w b l l n

(22)

(23)

(24)

Выражение (24) — это тоже формула Литтла, но для полного времени пребывания заявок в системе.

И наконец, отметим функцию распределения времени ожидания:

	1	t
w t 1 e		(25)

График этого распределения имеет следующий вид: w

1

=1 –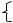

t

Рис. 21. График функции распределения времени ожидания.

где длина очереди в начальный момент времени определяется вероятностью простоя обслуживания прибора .

Кафедра математического обеспечения компьютерных систем. ОНУ им. И.И. Мечникова.

Е.В.Малахов. Имитационное моделирование. Конспект лекций.	22

Система М/М/N

Обозначение говорит о том, что на вход системы поступает простейший поток событий,

время обслуживания имеет показательное распределение, количество каналов в приборе — N.

Предполагается, что каналы в приборе идентичны,

1

очередная заявка захватывает первый свободный канал.

Переход системы

в

старшие состояния будет

обуславливаться

только

интенсивностью входного

N

потока, поэтому

i

, где i 1, n .

Переход системы в младшие состояния связан с

Рис. 22. СМО M/M/N.

освобождением каналов,

поэтому если канал один, то

интенсивность обслуживания равна , но если в приборе N>1 каналов, из которых занято i, то

интенсивность обслуживания возрастет в i раз и равна i до тех пор,				пока i N, после чего
остается постоянной:
i	i ,	при	0 i N ,
			i N .
	N ,	при

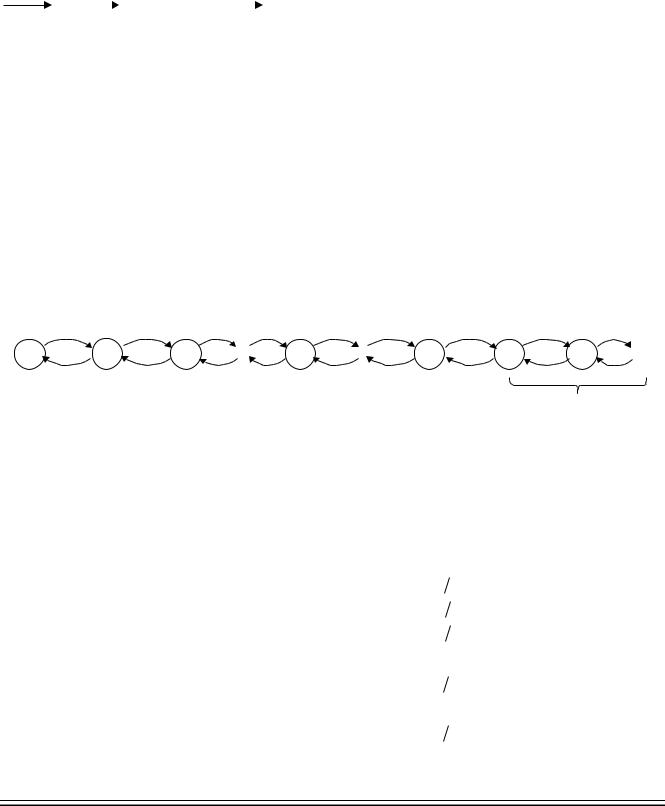
Граф марковского процесса будет выглядеть следующим образом:

0	1	2			i			N-1	N	N+1
		2	3	i		(i+1)	(N-1)	N	N		N
									появляется очередь заявок

Рис. 23. Граф марковского процесса СМО M/M/N.

В этой системе нас интересует N-ое состояние, т.е. состояние, в котором количество заявок и каналов совпадает. С этого момента появляется очередь заявок к обслуживающему прибору.

Уравнения Колмогорова-Чепмена для данной системы имеют вид:

P0 P1 0

P1 P0

P P 2 P 0

0

1

2

2 P1

P0 2 P2 3 P3 0

P2

P

3 P

3

2

P

i P i 1 P

0,

где

i 1, N

i 1

i

i

1

P i P

,

где

i 1, N

i

i 1

N Pi

Pi 1

N Pi 1 0,

где

i N

P

N P

1

,

где

i N

i

i

Кафедра математического обеспечения компьютерных систем. ОНУ им. И.И. Мечникова.

Е.В.Малахов. Имитационное моделирование. Конспект лекций.	23

		i
							i 1, N 1
			P0 ,			где
Pi	i!
			i				,
					P0 ,	где	i N .
				i N
	N !N

при нормирующем условии Pi 1

i 0

Из этого условия получим:

	N 1	i		i		1
P0
		i!		N !N	i N
	i 0		i N

(26)

(27)

Первая сумма данного выражения конечна, и ее легко вычислить. Поэтому рассмотрим вторую часть выражения, а именно — бесконечную сумму, которую обозначим через S2:

i

N

i

N

N

N

N

S 2

1

i N

i N N !N

N ! i N N

N !

N

N

Подставляя S2

в выражение для P0, получим:

1

N

1

i

N

P0

i!

N

i 0

N ! 1

				при		1, т.е. N
	2				N		N		1
				этот ряд сходится
N							N !
									1 N

(28)

Как уже было отмечено, в СМО M/M/N очередь заявок появляется тогда, когда все N

каналов заняты, т.е. i = N. Поэтому

i N

i

N 1

N 2

N 3

l i N Pi

P0

P0

2

P0 3

P0

N !N i N

N !N 2

N !N 3

i N

i N

N !N

N

2

3

N 1

(29)

P0

2

3

P0

N !

N

N

2

N

3

N !N 1

2

N

Среднее время ожидания определяется, как и для СМО M/M/1 формулой Литтла:

w l

СМО M/M/1/ /K

В тех случаях, когда на СМО накладываются ограничения либо на длину очереди, либо на количество источников нагрузки, то от трехбуквенной системы обозначения переходим к пятибуквенной: A/B/C/Q/K, где

Q — емкость очереди,

Кафедра математического обеспечения компьютерных систем. ОНУ им. И.И. Мечникова.

Е.В.Малахов. Имитационное моделирование. Конспект лекций.	24

K — число источников заявок.

В данной системе входной поток не является пуассоновским с бесконечным числом источников нагрузки, а создается конечной группой возможных клиентов. Итак,

1)В СМО имеется K источников нагрузки.

2)Требование находится либо в системе (в очереди или на обслуживании), либо вне системы в группе поступающих заявок.

Во втором случае момент времени поступления требования является случайной

величиной, распределенной по показательному закону со средним значением a 1 . Если в системе находится i заявок, то группа поступающих состоит из k-i требований. А т.к. все

клиенты, генерирующие заявки, не зависимы, общая интенсивность входного потока в этом состоянии равна (k-i).

В общем виде потоки в данной СМО выглядят следующим образом:

i	k i ,		где	0 i k
				i k
	0,		где
i	,	где	i 1,2,3,

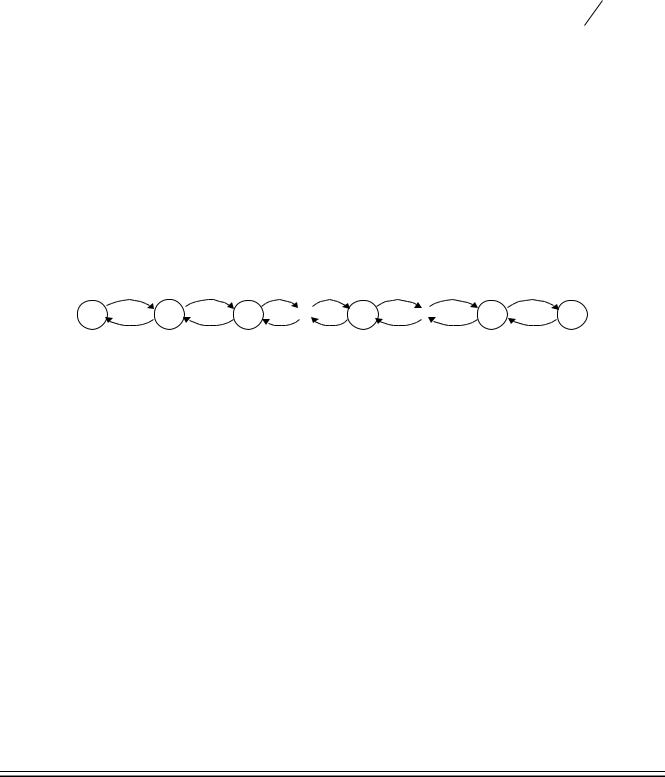
Граф данной системы будет иметь следующий вид:

K		(K-1)	(K-2)	(K-i-1)		(K-i)		2
0	1	2			i			K-1

Рис. 24. Граф марковского процесса СМО M/M/1//K.

Составим уравнения:

k P0 P1 0

k P k 1

P P 0

0

1

2

k!

i

Pi

P0 ,

1 Pi 1 k

i Pi

Pi 1

0

k i !

k i

0,

2 Pk 2 Pk 1

Pk 0

P 0

P

k 1

k

k

Из нормирующего условия Pi

1 получаем, что

i 0

k

k!

1

P0 i

i 0

k i !

K

где 0 i k

где i k.

Количество заявок в системе характеризуется геометрическим распределением, т.е.:

Кафедра математического обеспечения компьютерных систем. ОНУ им. И.И. Мечникова.

Е.В.Малахов. Имитационное моделирование. Конспект лекций.	25

niPi

i0k

Средняя длина очереди l = n - .

Система M/G/1

Теперь рассмотрим систему более общего вида M/G/1. Входным потоком в эту систему является простейший поток событий, в системе одноканальный обслуживающий прибор и произвольное распределение времени обслуживания. G не означает, что данный параметр невозможно описать, а говорит о том, что данный поток может быть любым из ранее

определенных либо он может определяться какой-либо функцией аналитика.

В первом случае система вырождается в одну из более простых систем (M/M/1, M/Ек/1,

M/Нк/1) и, соответственно, выкладки для нахождения их характеристик являются частными случаями решения для системы M/G/1. Поэтому G и называется генеральным распределением

или распределением общего вида.

Системы с экспоненциальным временем обслуживания заявок была рассмотрена ранее:

СМО M/M/1 и M/M/N. Системы с эрланговым распределением времени обслуживания заявок,

например, M/E3/1 может выглядеть следующим образом (Е3 — поток Эрланга 3-го порядка):

Входной поток простейший с интенсивностью .
А обслуживающий прибор можно представить так, как
представлялся генератор потока Эрланга k-го порядка — в виде	3		3	3
последовательной марковской цепи, интенсивности переходов	3
между состояниями которой равны k (в данном случае k = 3).				3
		3

			Коэффициент				вариации	такого	распределения:
			1			0.58			Рис. 25. Граф марковского
									процесса СМО M/E3/1.
	b
				k

Возникает вопрос: "Что общего между этой системой, системой M/M/1 и остальными,

аналогичными им?"

Для ответа на него и описывается система M/G/1.

Не углубляясь в математические выкладки и преобразования для получения величин,

характеризующих эту систему, отметим два важных результата, известных как формулы Поллачека-Хинчина.

Среднее время ожидания в очереди для системы M/G/1:

Кафедра математического обеспечения компьютерных систем. ОНУ им. И.И. Мечникова.

Е.В.Малахов. Имитационное моделирование. Конспект лекций.			26
w	b 2
		,	(30)
	2 1

где — интенсивность входного потока,

b(2) — второй начальный момент длительности обслуживания заявок 1.

Представим второй начальный момент длительности обслуживания через коэффициент

вариации b: b 2 D b E 2 b 2

b2 b b 2

b2

b2 1 b2

.

Подставляя это выражение в (30), получим:

w

b2 1 2

b 1 2

2 2 1

b

b

b

(30a)

2 1

2 1

2 1

Применяя формулу Литтла для количества заявок в СМО, получим:

	n u w b 2	1 b2		(31)
		2 1

Это формула Поллачека-Хинчина для среднего числа заявок в системе.

1 2

Средняя длина очереди, соответственно, l n 2 b

2 1

Теперь проверим: если коэффициент вариации равен 1, то имеем:

2

2

n

; l

,

1

1

1

что

соответствует экспоненциальному

распределению

w

длительности обслуживания, т.е. системе M/M/1.

Зависимость времени ожидания от загрузки прибора явно

2

2 > 1

нелинейна и для различных коэффициентов вариации имеет

следующий вид:

1

Для других общих случаев СМО с одноканальным

прибором

(G/M/1, G/G/1)

практически

не существует

аналитических методов получения точных характеристик. Для

1

таких систем единственным методом получения точных оценок

Рис.

26. Зависимость времени

является метод имитационных ошибок.

ожидания от загрузки прибора.

x dx , где f(x) — плотность

1 i-ый начальный момент случайной величины x определяется как x i

x i f

вероятности этой величины. Кстати,

x 1 E x .

i-ый центральный момент случайной величины x

определяется как

x i x x 1 i f x dx .

В частности,

x 2 D

.

x

Кафедра математического обеспечения компьютерных систем. ОНУ им. И.И. Мечникова.

Е.В.Малахов. Имитационное моделирование. Конспект лекций.	27

Неоднородные СМО

До этого мы полагали, что существует единственный входной поток, в котором все заявки однотипны: поступают с одной интенсивностью, имеют одинаковое среднее время обслуживания и т.д.

Теперь рассмотрим систему M/G/1 следующего вида:

a) в систему поступает М простейших потоков событий с интенсивностями 1, ..., М. Эти

M

потоки образуют суммарный пуассоновский поток с интенсивностью i ;

i 1

b)заявки, входящие в i-ый поток, называются заявками i-го типа и характеризуются различными начальными моментами времени длительности обслуживания. bi и bi(2)

соответственно.

Загрузка прибора, создаваемая заявками i-го типа i	i bi .
	M
Причем, загрузка создаваемая суммарным потоком	R i должна быть <1 (условие
	i 1

существования стационарного режима). Соответственно коэффициент простоя прибора определится как 1 R .

Остальные характеристики

для

каждого потока

определяются аналогичным образом:

li i wi , ni

i ui

M

Среднее время

ожидания

wср одной заявки

из

суммарного потока wср wi Pi

, где

i 1

P

i

—

вероятность

того,

что

поступившая

заявка является заявкой i-го

типа.

i

1

M

1

M

M

Соответственно, wср

wi i

li . Если li

lср

— средняя длина очереди или среднее

i 1

i 1

i 1

число заявок всех типов, находящихся в очередях, то

wср lср — формула Литтла для неоднородного потока заявок.

В любой физической системе нельзя получить "что-либо из ничего". То же самое относится к СМО с приоритетами — при изменении дисциплины обслуживания время ожидания заявок в очереди сокращается для одних типов заявок за счет увеличения времени ожидания заявок других типов. Для систем с одним обслуживающим прибором Леонард Клейнрок свел это утверждение к закону сохранения времени ожидания, который имеет следующее математическое выражение:

Кафедра математического обеспечения компьютерных систем. ОНУ им. И.И. Мечникова.

Е.В.Малахов. Имитационное моделирование. Конспект лекций.		28
M
i wi	const ,	(32)

i 1

где i — загрузка прибора заявками i -го типа, wi — их время ожидания в очереди.

Причем, эта сумма не зависит от дисциплины обслуживания.

Условия выполнения закона:

1)на вход поступает простейший поток событий, и длительность обслуживания не зависит от параметров входного потока;

2)рассматриваются СМО без отказов 1;

3)если используемая дисциплина обслуживания допускает прерывание обслуживания заявок,

то дообслуживание происходит по экспоненциальному закону.

СМО без приоритетов (СМО БП)

При бесприоритетном обслуживании заявки не имеют привилегий на досрочное обслуживание и выбираются из очереди в режиме FIFO (First In — First Out: первый вошел — первый вышел), LIFO (Last In — First Out: последний вошел — первый вышел), либо RAND (Random: случайным образом). Эти три бесприоритетные дисциплины характеризуются одинаковым средним временем ожидания, но дисциплина FIFO минимизирует дисперсию времени ожидания. Вследствие этого, коэффициент вариации времени ожидания для FIFO

меньше: wFIFO wLIFO wRAND . Поэтому при анализе рассматривается режим FIFO.

Итак, если в систему поступает М простейших неоднородных потоков с параметрами i, bi, bi(2), то средняя длительность пребывания заявки в очереди для всех классов одинакова:

M

i bi 2

w

БП

i 1

,

(33)

2 1 R

M

где R i

1 — суммарная

загрузка

прибора

создаваемая всеми потоками

(условие

i 1

стационарности системы).

b( 2 ) , в свою очередь, равно

b2

1

2 , где i — коэффициент вариации длительности

i

i

i

обслуживания.

Время же пребывания в СМО для каждого класса отличается:

ui uj, при i j,

и равно

ui w bi .

Т.е. ui отличаются

на

среднюю

длительность

обслуживания

заявок

1 Отказ — это возможность покидания СМО заявками или блокировка заявок в СМО. Т.е. если обслуживающий прибор свободен, то заявка сразу же поступает в него.

Кафедра математического обеспечения компьютерных систем. ОНУ им. И.И. Мечникова.

Е.В.Малахов. Имитационное моделирование. Конспект лекций.	29

соответствующего класса.

СМО с относительными приоритетами (СМО ОП)

При рассмотрении подобных систем заявкам каждого класса назначаются приоритеты в виде целых положительных чисел 1, 2, 3, … . Причем, с ростом номера приоритет уменьшается,

т.е. 1 — самый высокий.

Относительные приоритеты играют роль только при выборе заявок из очереди. В момент выбора сравниваются приоритеты заявок, находящихся в состоянии ожидания, и обслуживание предоставляется заявке с наиболее высоким приоритетом (например, 4). Если в процессе обслуживания заявки поступают требования с более высокими приоритетами (например, 1, 2,

или 3), обслуживание текущей заявки не прерывается, а поступившие заявки направляются в очередь.

Данный метод используется, например, при выделении квантов времени в мультизадачных системах, при выборе абонентов в сетях, клиентов в организациях и пр.

Итак, пусть в систему поступают M ППС с интенсивностями i, i 1,M и

длительностями обслуживания, которые описываются первыми и вторыми начальными моментами bi, bi(2) соответственно. Тогда время ожидания заявок с относительным приоритетом k, где k 1,M , определится как дробь:

					M
					i bi 2
			wОП		i 1			,	(34)
				2 1	R k 1 1 R k
			k
где
	k
R k i
		1
	i 1		— суммарная загрузка создаваемая i-ми классами заявок, при этом R0 = 0,
	k 1
R k 1	i
	i 1

1 Rk — простой прибора, вызванный "непоступлением" заявок всех k типов,

1 Rk 1 — простой, вызванный заявками всех потоков до k-го типа, кроме того, который мы

рассматриваем (т.е. всех заявок с большим приоритетом).

Проанализируем соотношения между временем ожидания заявок с различными приоритетами. При увеличении приоритета k 1,M 1 на единицу, время ожидания изменится

на величину

ОП

1

1

1 M

2

2

w

wk 1 wk

, где C

i bi

1 i

C

1

Rk

1 Rk 1

1

Rk 1 1

R k

2 i 1

Кафедра математического обеспечения компьютерных систем. ОНУ им. И.И. Мечникова.

Е.В.Малахов. Имитационное моделирование. Конспект лекций.	30

Нас интересует знак wОП, т.к. C — величина положительная, рассмотрим выражение в

скобках:

1

1

1 R k 1 1 R k 1

R k 1 R k 1

1 R

k

1 R

k 1

1 R

k 1

1 R

k

1 R

k

1 R

k 1

1 R

k 1

1 R

k

1 R

k 1

1 R

k 1

В знаменателе все сомножители также величины положительные, следовательно, знак

wОП зависит только от числителя:

Rk 1 Rk 1 1 2 k 1 k k 1 1 2 k 1 k k 1

Но k k 1 0 ,

wk wk 1

k

.

следовательно,

1,M 1

Таким образом,

время

ожидания заявок с k-м приоритетом меньше чем время ожидания заявок с (k+1)-м приоритетом.

Т.е. функция зависимости времени ожидания от приоритета является монотонно возрастающей.

Теперь сопоставим время ожидания заявок с ОП со временем ожидания при бесприоритетном обслуживании. Если k = 1 то формула (34) вырождается до следующей:

			M
			i bi 2
	wОП		i 1			(34a)
			2 1 1
	1

Обратите внимание, что формулы (30), (34) и (34а) отличаются только своими

знаменателями. Причем,

1 1 1 R 1 RM 1 1 RM для случая k = M

Следовательно, w1ОП wБП wMОП .

Т.е. введение относительных приоритетов приводит к уменьшению времени ожидания заявок с высоким приоритетом и увеличению времени ожидания заявок с низким приоритетом по сравнению с ДО БП.

Исследуем влияние суммарной загрузки R

системы на время ожидания заявок с различными приоритетами.

	wОП
wk	M
wБП	FIFO
wОП	ОП
1
0 1	M k

Рис. 27. Зависимость времени ожидания в очереди заявок с относительными приоритетами.

Кафедра математического обеспечения компьютерных систем. ОНУ им. И.И. Мечникова.