Перечень вопросов и практических задач
Тема 1: Элементы линейной алгебры
Матрицы и действия над ними.
Матрица – это прямоугольная таблица каких-либо элементов. Матрицы обычно обозначают прописными латинскими буквами A,B,C….
Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной.
Если в матрице один столбец или одна строка, то такие матрицы также называют векторами.
Теперь переходим непосредственно к изучению действий с матрицами:
1)Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу)
Для этого вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак.
2)Действие второе. Умножение матрицы на число.
Для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число.
3)Действие третье. Транспонирование матрицы
Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.
4) Действие четвертое. Сумма (разность) матриц.
Не все матрицы можно складывать. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были одинаковыми по размеру.
Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы.
Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.
5) Действие пятое. Умножение матриц.
В тетради с лекциями есть нормальное определение о произведение матриц и о обратной матрице, но так как у меня давно уже нет этой тетради (ибо я ее уже давно пропил), то учите это бесформенное говнище или найдите лучше.
Произведением матрицы А m на n на матрицу B n на k называется матрица C m на k такая, что элемент матрицы C, стоящий в i-ой строке и j-ом столбце, т.е. элемент C ij, равен сумме произведений элементов i-ой строки матрицы A на соответствующие элементы j-ого столбца матрицы B.
Чтобы матрицу можно было умножить на матрицу нужно, чтобы число столбцов матрицы равнялось числу строк матрицы.
Пример:
Умножить
матрицу 
на
матрицу 
Я
буду сразу приводить формулу для каждого
случая:
–
попытайтесь
сразу уловить закономерность.
Умножить
матрицу 
на
матрицу 
Формула: 
6) Действие шестое. Нахождение обратной матрицы.http://www.mathprofi.ru/kak_naiti_obratnuyu_matricu.html
Обратную
матрицу 
можно
найти по следующей формуле:
,
где 
–
определитель матрицы 
, 
–
транспонированная матрица алгебраических
дополнений соответствующих элементов
матрицы 
.
Пример:
Найти
обратную матрицу для матрицы 
1)Сначала находим определитель матрицы.
2) Находим матрицу миноров.
–
матрица
миноров соответствующих элементов
матрицы 
.
3)
Находим матрицу алгебраических
дополнений 
.
Это
просто. В матрице миноров нужно ПОМЕНЯТЬ
ЗНАКИ у
двух чисел:
4)
Находим транспонированную матрицу
алгебраических дополнений 
.
–транспонированная
матрица алгебраических дополнений
соответствующих элементов матрицы 
.
5) Ответ.
Вспоминаем
нашу формулу 
Всё
найдено!
Таким
образом, обратная матрица:
1.2. Понятие определителя и его свойства. Вычисление определителей.
Определитель матрицы, — число, соответствующее квадратной матрице и полученное путем ее преобразования по определенному правилу.
Свойства определителя:
1)При транспонировании матрицы величина её определителя не меняется.
2)Если две строки (или два столбца) определителя поменять местами,
то определитель сменит знак.
! Помните, речь идёт об определителе! В самой матрице переставлять ничего нельзя!
Сыграем
в кубик-рубик с определителем 
.
Поменяем
первую и третью строку местами:
Определитель сменил знак.
3) Из строки (столбца) определителя можно вынести общий множитель.
!!! Внимание! В правиле речь идёт об ОДНОЙ строке или об ОДНОМ столбце определителя. Пожалуйста, не путайте с матрицами, в матрице множитель выносится/вносится у ВСЕХ чисел сразу.
4) Если две строки (столбца) определителя пропорциональны
(как частный случай – одинаковы), то данный определитель равен нулю.
5) Определитель с нулевой строкой (столбцом) равен нулю.\
Пример: 
Вычислить определитель – это значит найти число.
Определитель матрицы «три на три» можно раскрыть 8 способами:
1)Определитель можно раскрыть с помощью формулы:
2) Способ Саррюса или способ «параллельных полос». Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:
Множители,
находящиеся на «красных» диагоналях
входят в формулу со знаком «плюс».
Множители,
находящиеся на «синих» диагоналях
входят в формулу со знаком минус:
3-8) Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения(минор). Пример:
четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).
1.3. Системы линейных уравнений. Основные понятия и определения.
Тут тоже лучше использовать тетрадь вместо этой херни.
Система линейных уравнений— это объединение изnлинейных уравнений, каждое из которых содержитkпеременных. Записывается это так:
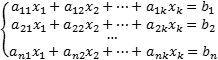
В матричной
форме записи эта система уравнений
имеет вид 
,
где
-
основная матрица системы,
-
матрица-столбец неизвестных переменных,
-
матрица-столбец свободных членов.
Решить систему уравнений – это значит найти множество её решений. Решение системы представляет собой набор значений всех входящих в неё переменных, который обращает КАЖДОЕ уравнение системы в верное равенство.
1.4 Методы решения систем линейных уравнений (метод Крамера и Гаусса).
– Решение системы линейных уравнений методом подстановки («школьный метод»);
– Решение системы методом почленного сложения (вычитания) уравнений системы;
– Решение системы по формулам Крамера;
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля.
Рассмотрим систему уравнений 
На первом шаге вычислим определитель 
,
его называют главным определителем
системы.
Если 
,
то система имеет единственное решение,
и для нахождения корней мы должны
вычислить еще два определителя:
и
Корни
уравнения находим по формулам:
,
– Решение системы с помощью обратной матрицы;
– Решение системы методом Гаусса.
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные систем.