Деденко Методы обработки резултатов ядерно-физического експеримента 2008

ЗАДАНИЯ

1. Вычислить функции:

y(x) := x3 +3 x2 −5 x +1,

g(x) := x3 +2 x2 −7 x +3 и вывести на экран их графики в про-

межутке от -10 до 10 с шагом 0.1. (Разобрано подробно в качестве примера.)

Решение.

Набрать x:=-10,-9.9 ..10

Действие	Пояснение
x	Ввод параметра цикла x
Shift ;	Оператор присвоения
-10	Начальное значение x
,	Разделение двух чисел
-9.9	Следующее	значение x,
	(разность первого и второ-
	го значенийx	показывает
	шаг вычислений)
;	Ввод двух точек (специ-
	альный оператор)
10	Конечное значение x

Набрать y(x) := x3 +3 x2 −5 x +1. Набрать g(x) := x3 +2 x2 −7 x +3 .

Набрать @ при помощи комбинации клавиш Shift 2. Появится заготовка для графика.

Заполнить центральные квадратики: y(x) и x – по вертикали и горизонтали соответственно.

Убрать курсор с поля графика вправо или вниз. Щелкнуть мышью в любом месте документа.

Чтобы изменить формат графика, тип линии (линия, точки, прямоугольники и т. д.), нужно дважды щелкнуть мышью на нем.

21

Если подвести указатель мыши к его нижней или правой границе, то указатель мыши примет вид двойной стрелки; удерживая при этом нажатой левую кнопку мыши и перемещая этот курсор по экрану, изменяем размер графика.

2.	Построить функцию	y(x) := exp				−	x2	sin (5 x) и вы-
						10
вести на экран ее график в пределах от -10 до 10 с шагом 0.1.
		3 −5		1		2 4			−1
3.	Ввести две матрицы:		9					−3	9
		2		10	и 5					.
			−1					8	6
		4		7		1

ипровести с ними следующие действия:

1)транспонирование каждой матрицы;

2)сложение матриц;

3)вычитание матриц;

4)умножение матриц;

5)вычисление определителя каждой матрицы;

6)вычисление обратных матриц.

Для упрощения задания присвойте матрицы переменным и операции выполняйте над переменными, чтобы многократно не переписывать матрицы.

4.Вычислить интеграл: ∫7 3 ln(x) sin(x)dx .

1x

5.Вычислить сумму квадратов всех четных чисел от 0 до

100.

6. Найти

корни

уравнений

x3 +3 x2 −5 x = −1,

x3 −sin (3 x)= e−x . Метод решения найти, используя HELP (най-

дите несколько способов решения, для первого уравнения их три, а для второго два). Не пытайтесь набрать эти уравнения так, как вы их видите здесь, т.е. со значением в правой части, используйте HELP или QuickSheets для нахождения правильной формы запи-

си!).

22

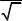
7. Решить систему уравнений

3 x + 5 y = 2 4
	2	x − 7	y	= 1 5 .

8. Найти аналитически производные функций y(x) := x3 +e−x + x e−x

y(x) := sin(x) y(x) := tan(x)

y(x) := 1x

z(x, y) := x1/3 + y3 (сначала z по x, затем исход-

ную z по у)

z(x, y) := x1/3 y3 (сначала z по x, затем исход-

ную z по у)

9. Построить график функций (использовать функцию if)

x		−∞ < x <10
y(x) =	2	.
x		10 ≤ x < +∞

10. Найти k корень уравнения

k

0.5 = ∫x e−xdx.

0

11. Найти интегралы функций (аналитически)

	y(x) := cos(x)
	y(x) := cos(x)		−		sin(x)
		ln(x)			x ln(x)2
	y(x) :=	cos(x)2			.
		1+sin(x)

23

Лабораторная работа № 2

ИЗУЧЕНИЕ ОСНОВНЫХ РАСПРЕДЕЛЕНИЙ ФИЗИЧЕСКИХ ВЕЛИЧИН

Целью работы является практическое изучение студентами основных законов распределения случайных величин. За время работы студенты овладевают практическими навыками программирования функций распределения, функций плотности распределения и основных характеристик случайных величин, а также моделирования распределения с заданными параметрами в диалоговом режиме с помощью пакета “MATCAD”.

ВВЕДЕНИЕ

Случайной называется величина, которая в одних и тех же условиях может принимать различные значения. Случайные вели-

чины бывают дискретные и непрерывные.

Все дискретные случайные величины характеризуется вероятностью P появления того или иного значения. Такая вероятность вычисляется для дискретных величин по формуле P=m/n, где m – количество испытаний (появлений), когда выпало это фиксированное значение (число), n – полное число испытаний.

Для непрерывных случайных величин используют понятие

плотность вероятности
f (x) = lim	P(x −	x 2 ≤ x ≤ x + x 2)	,
		x
x→0
где f (x − x 2 < x < x +		x 2) – вероятность того, что случайная
величина примет значения в интервале от x −			x 2 до x + x 2 .

Биноминальное распределение описывает дискретные со-

бытия следующего типа: в результате эксперимента событие либо наблюдается (происходит), либо нет (не происходит). Пусть, например, произведено n испытаний. Вероятность произойти некоторому событию А есть р, а вероятность ему не произойти есть 1-р.

Вероятность P(m) выпадения события А m раз в серии из n экспериментов есть:

P(m) = mn Cipm (1− p)n−m ,

24

	где mn C – число сочетаний из n по m: mn C =	n!		.
		m!(n −m)!

Это распределение и называется биноминальным.

Если число проведенных экспериментов n будет расти до бесконечности n →∞ , то биноминальное распределение превратиться в пуассоновское. Для распределения Пуассона вероятность произойти m событиям равна:

P(m) = μm e−μ , m!

где μ – среднее число событий за время проведения эксперимента. Для непрерывных случайных величин довольно распространенным является распределение Гаусса (его также называют нор-

мальным).

Для нормального распределения функция плотности вероятности имеет вид:

	f (x) =		1	e−	( x−μ)2
					2σ2	.
		σ	2π

Такая функция определяется заданием двух параметров: μ – математическое ожидание и σ – дисперсия. Если параметры μ = 0, σ = 1, то такое нормальное распределение называется стандарт-

ным.

Если x1, x2 ,..., xn – независимые нормальные случайные ве-

личины, подчиняющиеся стандартному нормальному распределению, то сумма квадратов этих величин носит название распределения χ2 с n степенями свободы.

χn2 = x12 + ... + xn2 .

Плотность вероятности распределения χ2 определяется выражением:

			1						n	−1			χ	2
f ( χn	2 ) =							(χ2 )2			exp	−				,
		n											2
					2	n	2
		Γ
			2
							25

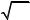
где Γ(x) – гамма-функция, Г(х) = ∞∫tx−1e−t dt

0

Математическоеожиданиеидисперсияравнысоответственно:

E{χ2} = n; σ2(χ2) = 2n.

При n > 30 распределение χn2 можно считатьнормальным. Если y, а также y1, y2,...,yn – независимые величины, имею-

щие нормальное распределение с математическим ожиданием равным нулю, то величина t подчиняется распределению Стьюдента

с числом степеней свободы n: t =			y
	1				1
			n
				2		2
			∑yi
	n i=1

Плотность распределения Стьюдента, представляющая собой отношение нормально распределенной величины к величине, подчиняющейся распределению χ2, имеет следующий вид:

n +1

1

Γ

x

2

−

n+1

Sn (x)=

2

+

2

1

,

πn

n

n

Γ

2

где n – число степеней свободы.

Распределение Стьюдента при большом числе степеней свободы переходит в стандартное нормальное распределение.

При использовании системы MathCAD данные плотности распределения можно ввести при помощи встроенных функций системы MathCAD.

Любой закон распределения определяется следующими величинами (моментами).

Основные моменты случайной величины

1. Математическое ожидание случайной величины x, кото-

рое можно рассчитать по следующим формулам:

μ = ∑xiP(x) для дискретной величины,

26

μ = ∫xif (x)dx для непрерывной величины.

2. Центральные моменты

а) дисперсия

D = ∑(x −μ)2 P(x) для дискретной величины,

D= ∫(x −μ)2 f (x)dx для непрерывной величины;

b)эксцесс

E = ∑(x −μ)3 P(x)	для дискретной величины,
E = ∫(x −μ)3 f (x)dx	для непрерывной величины;
с) момент четвертого порядка
M 4 = ∑(x −μ)4 P(x)	для дискретной величины,

M 4 = ∫(x −μ)4 f (x)dx для непрерывной величины.

Свойства моментов

1.Математическое ожидание

а) для биноминального распределения

	n−1	(n −1)!
	M = np∑			ps (1− p)n−s−1;
		(n − s −1)!s!
	s=0

б) для пуассоновского распределения M = μ; в) для нормального распределения M = μ.

2.Дисперсия

а) для биноминального распределения D = np(1− p) ; б) для пуассоновского распределения D =μ ;

в) для нормального распределения D = σ2 .

27

3.Эксцесс

	а) для биноминального распределения E =	1−2 p	;
		np(1− p)

б) для пуассоновского распределения E = μ ;

в) для нормального распределения E = 0 .

Следует также отметить важное соотношение MD4 = 3 для стандартного нормального распределения. Условия равенства нулю эксцесса и выполнения соотношения MD4 = 3 обычно принимают

для контроля правильности аппроксимации данного распределения распределением Гаусса.

Приведенные выше соотношения справедливы для генеральной совокупности данных (число измерений стремится к бесконечности). На практике экспериментатор всегда имеет дело с выборкой ограниченного объема. Поэтому для анализа распределений параметры заменяют их оценками по имеющимся выборкам.

Аналогом математического ожидания является выборочная

средняя величина.

Для набора n значений случайной величины выборочное среднее равно:

x= 1 ∑n xi , если xi равновероятны, n i=1

или x =	1	n
		∑xi Pi , где Pi–вероятность проявления значения xi.
	n i=1

Если данные сгруппированы, т.е. указаны значения xi и частота принятия таких значений νi, то

	k
	∑vi xi		1	k	k
x =	i=1	=		∑vi xi ,	i =1,2,..., n , так как ∑vi = n ,
	k		n
	∑vi			i=1	i=1
	i=1
					28

где n – объем выборки; k – число значений, которые принимала случайная величина.

Аналогом дисперсии является выборочная дисперсия Sn2 , которая для выборки объема n имеет вид:

		1	n
	Sn2 =		∑(xi − x)2 (для равновероятных значений xi ).
		n −1 i=1

Наиболее важной теоремой математической статистики является центральная предельная теорема, которая формулируется следующим образом.

Пусть случайная величина х имеет математическое ожидание

μ и дисперсию σ2 . Если σ2 конечна, то при стремлении объема выборки случайных величин x к бесконечности распределение вы-

борочного среднего x будет стремиться к нормальному со средним μ и дисперсией σ2/n.

Следует подчеркнуть, что центральная предельная теорема выполняется независимо от вида распределения величины x.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1.Построить графики функций плотности распределения для биноминального, пуассоновского и нормального распределений (значения параметров согласовать с преподавателем). Исследовать характер изменения функций плотности распределения при вариации параметров. Функции плотности ввести двумя путями: при помощи приведенных формул и при помощи встроенных функций системы MathCAD. Убедится в их идентичности.

2.Вычислить значения моментов распределений и их отношений по приведенным формулам из раздела «Основные моменты случайной величины» (численно покажите справедливость приведенных свойств для моментов).

3.На одном рисунке построить графики функции плотности распределения для пуассоновского и нормального распределений с одинаковыми параметрами (параметры согласовать с преподавателем). Убедится, что при больших μ пуассоновское распределение можно заменять нормальным. Определить параметры такого нормального распределения.

29

4.С помощью встроенных функций MathCAD ввести распределение Стьюдента и χ2 и показать, что при больших n данные распределения переходят в нормальное (плотности построить на одном графике).

5.С помощью функции rnorm(n,μ,σ) получить выборку объемом n=100 нормально распределенных случайных величин. Определить среднее и выборочную дисперсию. Проверить выполнение соотношения M4/D=3.

30