Елтаренко Исследование операцыи 2007

2. Управляемый объект имеет 4 возможных состояния. Через ка-

ждый час	производится снятие информации					и перевод объекта из
одного состояния		в другое в		соответствии		со следующей мат-
рицей вероятностей переходов:
	S1		S2		S3		S4
S1	0,3		0,4		0,0		0,3
S2	0,2		0,2		0,4		0,2
S3	0,4		0,3		0,2		0,1
S4	0,2		0,3		0,4		0,1
Найти	вероятности нахождения объекта в каждом из состояний

после второго часа, если в начальный момент он находился в состоянии S3.

3. По заданным коэффициентам системы уравнений Колмогорова составить размеченный граф состояний. Определить коэффициенты А, В, С, Д в уравнениях:

-А Р1 + 4 Р2 + 5 Р3 = 0

-В Р2 +	4 Р1 + 2 Р4 = 0
-С Р3 +	2 Р2 +	6 Р1 = 0
-Д Р4 +	7 Р1 +	2 Р3 = 0.

4. Физическая система имеет 4 состояния. Размеченный граф со-

стояний приведен ниже.
	6
S1		S2
4	5	3
S3		S4

5

Определить предельные вероятности состояний системы.

30

1.4. Пуассоновские СМО

В пуассоновских СМО входной поток заявок – пуассоновский, т.е. f t et , а время обслуживания распределено по экспоненциаль-

ному закону t

e t .

1.4.1. Одноканальные пуассоновские СМО

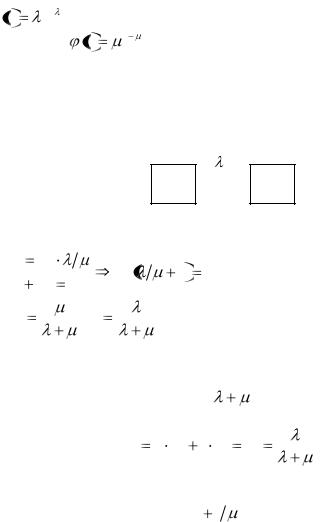
СМО без очереди (N=0). Используем теорию процессов гибели и

размножения для определения вероятностей P , P (рис. 1.9).

0 1

S0 S1

μ

Рис. 1.9. Размеченный граф СМО без очереди

	P	P
	1	0	P0	1 1;
	P	P 1
	1	0

P		; P		.
0	1

Вероятность отказа заявки в обслуживании равна P1 :

P .

отк

Среднее число заявок в системе равно:

L	0 P	1 P	P		.	(1.17)
s	0	1	1

Среднее время пребывания в СМО равно среднему времени об-

служивания:
Ws 1 ;	(1.18)

так как очереди в СМО нет, то

31

Wq 0, Lq 0.

Эффективный поток заявок определяется по формуле:

эфф	1	P		.
		отк

СМО с ограниченной очередью

Размеченный граф данного класса СМО представлен на рис. 1.10.

S0

S1

S2

...

SN 1

Рис. 1.10. Размеченный граф одноканальной СМО с ограниченной очередью

Конечное состояние в системе определяется максимальным числом мест в очереди плюс 1 канал обслуживания. Введем обозначение

. Система уравнений для нахождения предельных вероятностей Pn имеет вид:

P	P
1	0
P	P			2 P	(1.19)
2	1			0
P	P			n P
n		n 1		0
N 1
Учитывая, что Pn	1, получим уравнение для определения P0 :
n 0
N 1				N 1
	n P 1			P	n 1,
	0			0
n 0				n	0

32

откуда получим P0			1	, где	– любое, т.е. на отношение
	1		N 2

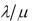не накладывается никаких ограничений. Вероятности Pn P0 n .

Определим среднее число заявок в СМО:

N+1

Ls n Pn

n=0

Обозначим через F(ρ)

N+1			n ρn
P				P
0				0
n=0
N+1	ρ	n 1		ρN+2
			1	ρ
n=0

N+1

nρn-1 .

n=0

F( )

, тогда

(1 ρN+2 )	(1	ρ)(N+2 )ρN+1
Fρ	(1	ρ)2
1 (N+1)ρN+2	(N+2 )ρN+1
(1	ρ)2	.

(1.20)

(1.21)

Подставив (1.20) в (1.21), получим:
(1	ρ)ρ1 (N+1)ρN+2	(N+2 )ρN+1
Ls	(1 ρN+2 )(1	ρ)2	. (1.22)

Отметим, что вероятность отказа равна вероятности последнего

состояния в размеченном графе:
P	P			ρN+1P ;
отк		N+1			0
эфф		(1	P ) .
				отк
Используя формулы Литтла (1.1 – 1.3), получим:
W				Ls		;		(1.23)
		s		λэфф
W		W			1		;	(1.24)
q			s		μ

33

				Lq Wq			эфф .			(1.25)
Рассмотрим частный случай, когда									, т.е.	1. В этом слу-
чае P	P	P	P	:
1	0	2	N 1
				P0	1			;
					N		2
				Pот к	1				.
						N	2

Основные характеристики СМО определяются по следующим

формулам:

L

N

1

;

s

2

1

1

N

1

;

эфф

N

2

N

2

W

N

1

N

2

N

2 ;

s

2 N

1

2

W

W

1

;

q

s

L

W

N

1

N

1

.

q

ýôô

q

2

N

2

СМО с неограниченной очередью. Так как СМО без отказов, то

Pот к 0 , а эфф .

Для получения формул расчета характеристик СМО воспользуемся формулами для СМО с ограниченной очередью.

		1 N 1	N 2	N 2
L lim					N 1	.	(1.26)
			N 2
s	N 0	1		1

34

Чтобы существовал предел,			необходимо выполнение условия
		1, которое означает,	что интенсивность обслуживания

должна быть больше интенсивности потока заявок, иначе очередь будет расти до бесконечности.

Отметим, что в СМО с бесконечной очередью

					P		1			.								(1.27)
		0
Предел (1.26) равен: Ls							, и тогда
		1
Ws	Ls														1	;		(1.28)
							(1					)
Wq	Ws	1					1			1							;	(1.29)
															(	)
										2
	Lq			Wq											.			(1.30)
							(			)

Рассмотрим вопрос о функции распределения времени пребывания в одноканальной СМО с бесконечной очередью при дисциплине очереди FIFO.

Время пребывания в СМО, когда в ней находится n заявок (система находится в состоянии Sn, равно сумме длительностей обслуживания n заявок. Так как время обслуживания распределено по экспоненциальному закону, то плотность функции распределения условной вероятности времени пребывания в СМО, когда в ней находится n заявок, определяется так же, как распределение Эрланга n порядка

(см. раздел 1.2.2)

f	Ws	( t)n	e	t
	n	n!

Искомая плотность функции распределения определяется выражением:

35

W

(

t)n

t

f (W )

f

s

P

e

P .

s

n

n

n!

n

n 0

n 0

С учетом (1.19) и (1.27),

f (Ws )

запишется в виде:

f (W )

( t)n

e t (1

) n

(1

)e

t

( t)n

n

s

n!

n!

n 0

n

0

e

t e t

f (Ws ) (1 )e( )t (1 )e (1 )t .

Видим, что f (Ws ) − экспоненциальное распределение с матема-

тическим ожиданием M(Ws )	1		1		, что совпадает с
	(1	)
(1.28).

Из того, что f (Ws ) − экспоненциальное распределение, следует

важный вывод: выходной поток заявок в одноканальной СМО с бесконечной очередью является пуассоновским потоком.

1.4.2. Многоканальные пуассоновские СМО

СМО с ограниченной очередью (N>0)

Размеченный граф данного класса СМО представлен на рис. 1.11.

S1		S2		S3		...	Sm		...		SN m
			2		3	m		m		m

Рис. 1.11. Размеченный граф многоканальной СМО с ограниченной очередью

Составим систему уравнений для определения предельных вероятностей состояний:

P	P	P	, где
1	0	0

36

P

P

2

P

2

2

2

1

0

3

P3

P2

3

P0

1 2 3

k

Pk

P0 , k 1, , m

k!

Pm 1

Pm

m

P

P

m

P

m 2

m 2

m 1

m

m 1

k

m N m

n m

P0

1

k!

m!

k 0

n m

N 1

1

N 2

n

n

0

1

P

m n m P , n m 1, , N m.

n

m

Введем обозначение

m

, тогда

m

P

n mP

n m

P (n m, , N m) , и

n

m

m! 0

k

P

P

(k

1, ,m

1) .

k

0

k!

Учитывая условие, что сумма всех вероятностей равна единице,

m 1		N m
т.е.	Pk	Pn 1, получим P0 :
k	0	n m
		m 1	k		m	1		N 1	1
		P0							.	(1.31)
			k!		m!		1
		k 0

Определим среднее число заявок в очереди:

N	N					m
L	nP	n	n P	, где P	P		;
q	n m		m	m	0	m!
n 0	n 0

37

N

n 1 .

L

P

n

(1.32)

q

m

n

0

G

Введем в рассмотрение функцию:

N

n

1

N 1

G

;

1

n 0

1

N 1

N 1 1

N

1 N 1 N

N

N 1

G

. (1.33)

1

1

2

Подставим (1.33) в (1.32):

m

1

N

N 1

N

1

N

L

P

.

(1.34)

q

m! 0

1

2

Вероятность отказа в обслуживании равна:

N

m

P

P

N P

P .

отк

N m

m

m!

0

Эффективный поток заявок:

эфф

1

P .

отк

Используя формулы Литтла, получим среднее время ожидания заявок в очереди:

Wq Lq .

эфф

Время в СМО отличается от Wq на время обслуживания:

Ws Wq 1 .

Наконец среднее число заявок в системе равно:

Ls Ws эфф .

Частный случай		1.
	m

Система уравнений для определения Pn примет вид:

38

k

Pk

P0, k 0, , m;

k!

P

n m P P , n m, , N m.

n

0

m

Определим P0 :

N m

N m

n m

Pn

Pm

NPm ;

n m 1

n m 1

m 1

k

m

1

P0

N

1 .

k 0

k!

m

Средняя длина очереди равна:

N

n

N

L

P

n

N

1 P .

q

m

2

m

n 0

m

Учитывая, что Pm

P0

, получим:

m!

m

N N

1

L

P

.

q

0

m!

2

СМО без очереди (N=0)

S0

S1

...

Sm

Рис. 1.12. Размеченный граф многоканальной СМО без очереди

Используя (1.31) при N 0 , получим:

	m	k	1
	P0		.
		k!
	k 0

Вероятность отказа в обслуживании равна:

		m
P	P		P .
отк	m	m! 0
	39