Beginning Algorithms (2006)

Chapter 8

To complete this class, you implement the remaining methods of the Queue interface. These are exactly the same as any other list-based Queue implementation:

public void clear() { _list.clear();

}

public int size() { return _list.size();

}

public boolean isEmpty() { return _list.isEmpty();

}

If you run the test, you will see that this implementation behaves exactly as expected. You can now move on to implementing a version of the priority queue that aims to eliminate all that brute-force searching!

How It Works

The unsorted list implementation of a priority queue is very simple. To enqueue an item, you simply use the internal list’s add() method to append it to the list. To remove an item from the queue, you simply iterate through all the items in the member list, remembering which of those scanned so far is the largest. At the end of the iteration, you return the largest item, removing it from the list as you do so.

Understanding the Sorted List Priority Queue

One way to avoid a brute-force scan of the whole list of items in your queue whenever dequeue() is called is to make sure the largest item is available more quickly by keeping the items in sorted order. In this way, the dequeue() method will be very fast, but you have to sacrifice a little more effort during enqueue() to find the right position to insert the new item.

The approach you use in the next Try It Out is to use an insertion sort mechanism during calls to enqueue() to place newly added items into sorted position in the underlying list. Calls to dequeue() will then be extremely simple — merely remove the largest item at the end of the list.

Try It Out

Testing and Implementing a Sorted List Priority Queue

In this section, we will implement a priority queue that uses an underlying list maintained in sorted order.

Extend AbstractPriorityQueueTestCase for our specific implementation, as shown here:

public class SortedListPriorityQueueTest extends AbstractPriorityQueueTestCase { protected Queue createQueue(Comparator comparator) {

return new SortedListPriorityQueue(comparator);

}

}

184

Priority Queues

The basic structure of this implementation is very similar to the unsorted version described previously in this chapter. Use the same instance members and an identical constructor:

public class SortedListPriorityQueue implements Queue { private final List _list;

private final Comparator _comparator;

public SortedListPriorityQueue(Comparator comparator) { assert comparator != null : “comparator cannot be null”; _comparator = comparator;

_list = new LinkedList();

}

...

}

Create the enqueue() method to scan backwards through the items in the list, finding the appropriate place to insert the new item:

public void enqueue(Object value) { int pos = _list.size();

while (pos > 0 && _comparator.compare(_list.get(pos - 1), value) > 0) { --pos;

}

_list.insert(pos, value);

}

You implement dequeue() by removing the last item from the list. Remember to throw an exception when the list is empty, as there is nothing to return:

public Object dequeue() throws EmptyQueueException { if (isEmpty()) {

throw new EmptyQueueException();

}

return _list.delete(_list.size() - 1);

}

You add a final few methods that are simple, with nothing different from the other Queue implementations you have seen:

public void clear() { _list.clear();

}

public int size() { return _list.size();

}

public boolean isEmpty() { return _list.isEmpty();

}

185

Chapter 8

That’s it for the sorted list implementation of a priority queue. Run the test and you will see that it meets the criteria you established for correct priority queue behavior. The next section addresses the most complex but most effective and practical version of a priority queue, based on a structure called a heap.

How It Works

The version of enqueue() you use in this implementation is a little more complex than your previous implementation. Its function is to find the appropriate position in the list where the new item should be inserted. It does this by scanning backwards through the items in turn until it either finds one that is smaller or comes to the beginning of the list. It then inserts the new item into the queue at this position. This ensures that at all times the largest item is at the end of the list.

The benefit of expending this extra effort is that the implementation of dequeue() has nothing to do except remove the last item from the list and return it.

Understanding Heap-ordered Priority Queues

A heap is a very useful and interesting data structure, so we will take our time in this section explaining how it works. After you grasp the concept, you can use a heap to implement an effective priority queue.

A heap is simply a binary tree structure in which each element is larger than its two children. This is known as the heap condition. In Figure 8-7, note that whichever node you look at, the element is larger than its children (if it has any).

X

M K

E A F D

D B

Figure 8-7: A heap.

Be careful not to think of a heap as being sorted, however, as it is not sorted at all. It does have a useful property that is of interest, however: By definition, in a heap, the largest item is sitting right at the top of the tree. The arrangement of the other items is of little interest to us. For example, notice that the smallest element in the heap (in this case, an A) is not on the bottom row of the tree as you might expect.

You might be wondering if there is a Heap interface or a Tree interface about to be defined and implemented. In this example, that won’t be our approach. This case uses a simple list to contain the heap structure. Figure 8-8 demonstrates a technique of numbering the elements in the heap such that you can easily find them by their index. You start at the top of the tree with index zero, and work top to bottom and left to right, counting as you go.

186

Priority Queues

	0	X
	1 M	2	K
3 E	4 A	5 F	6 D
7 D	8 B

Figure 8-8: Numbering the items in a heap for storage in a list.

This approach enables you to have a mental model of a tree structure in an implementation in which no tree structure exists at all. Figure 8-9 shows what the list would look like that contains our sample heap structure.

	0	X
	1 M	2	K
3 E	4 A	5 F	6 D
7 D	8 B

X	M K E A	F D D B
0		8

Figure 8-9: The heap structure contained in a list.

187

Chapter 8

To use your heap, you must be able to navigate the structure upwards and downwards. Therefore, if you know the index of an item, you need to be able to determine the index of its left child item and its right child item. You also need to be able to determine the index of its parent item. Here’s the way you do it:

The left child of the item at index X is at index (2 × X + 1).

The right child of the item at index X is at index (2 × X + 2).

The parent of the item at index X is at index ((X – 1) / 2); the item at index 0 has no parent, of course!

Refer to the figures in this section to satisfy yourself that these formulas work as you expect. The formula for the parent index of an item relies upon truncation of the result if the item in question is the right child of the parent. You’ll realize this if you try to access a list at index “3.5”!

Sink or Swim

To use the heap to build a priority queue, you need to be able to add items to it and remove items from it. That might sound obvious, but in order to perform each of those operations, you need to maintain the heap condition — that is, you need to make sure the heap is still a heap after you add or remove items from it.

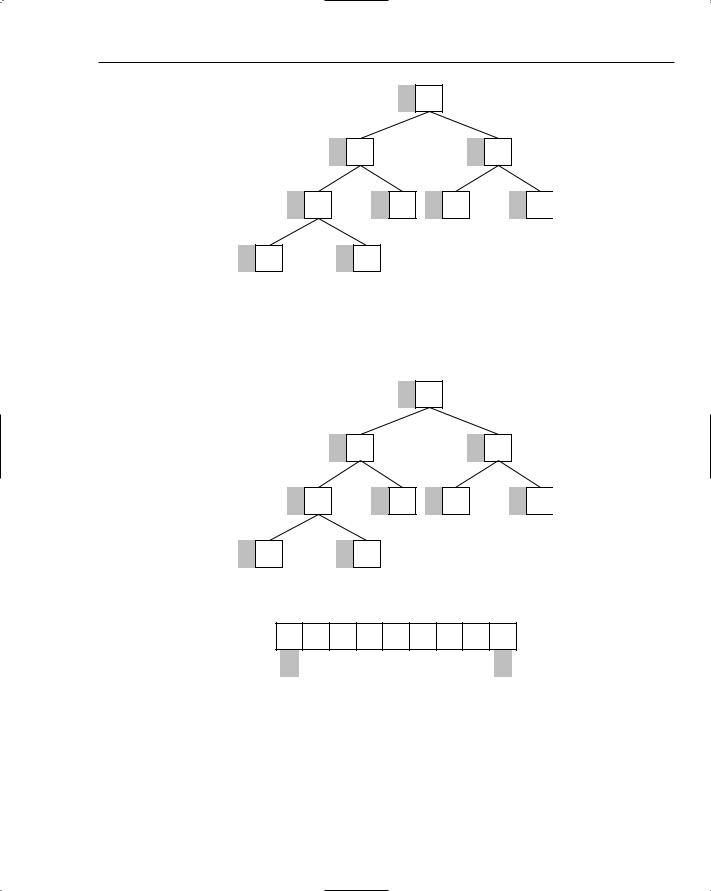
Let’s extend the sample heap by adding the letter P to it. You start by simply adding it to the bottom of the tree structure, as shown in Figure 8-10.

X

M K

E A F D

D B P

Figure 8-10: A new item is added to the heap, breaking the heap condition.

The heap is going to be stored as a simple list, so you just add the new item to the end. The problem is that now the heap is no longer a heap! This is because the parent (A) of the new item (P) is smaller than the item itself. To fix the heap and reestablish the heap condition, the new item must work its way up the tree structure until the heap condition is restored. This is called swimming to the top.

Swimming is a matter of exchanging an item with its parent if the parent is smaller, and continuing until the top of the heap is reached or a parent is found that is equal to or larger than the item doing the swimming. Figure 8-11 shows the situation after the new item has been swapped with its parent item.

188

Priority Queues

X

M K

E P F D

D B A

Figure 8-11: The new item is exchanged with its parent.

The heap condition is still not met because the new item (P) is larger than its parent (M). It needs to keep swimming. Figure 8-12 shows what happens when the new item is again swapped with its parent item.

X

P K

E M F D

D B A

Figure 8-12: The new item moves into final position in the heap.

The heap condition is now restored, and the heap is one element larger than it was before you added an item and maintained the heap condition. The next challenge is to do the same when removing the largest item from the heap.

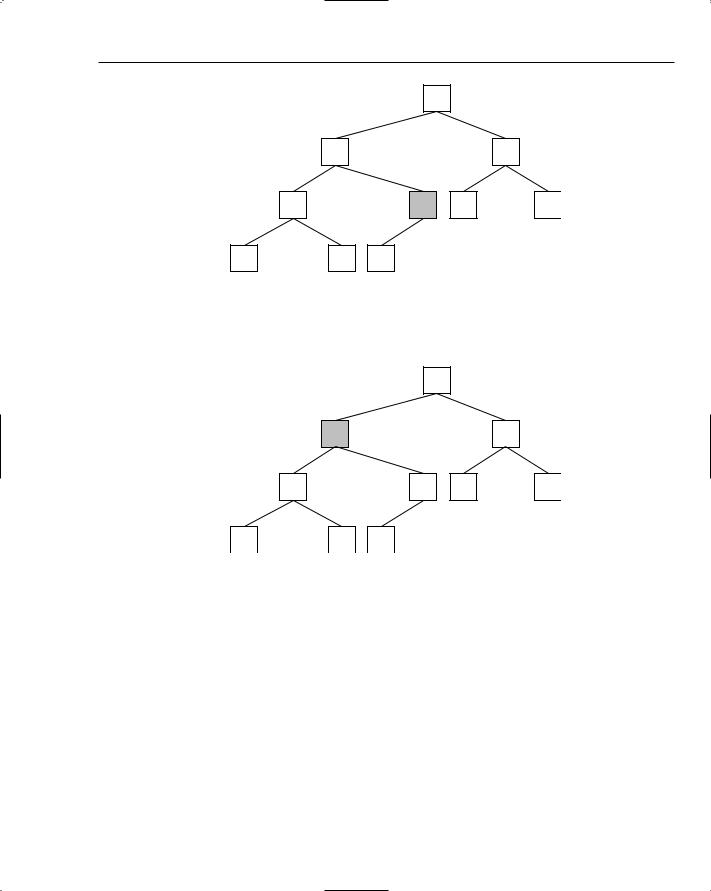
Locating the largest item is easy, but removing it is not so easy. If you just delete it from the underlying list, the tree structure is completely destroyed and you have to start again. (Feel free to try this as an experiment for your own enjoyment!) Instead, you can swap in the item at the bottom right of the tree, as shown in Figure 8-13.

189

Chapter 8

X

A

P K

E M F D

D B

Figure 8-13: The largest item is removed and the last item is put at the top.

Although the tree structure itself is still intact, the heap condition is once again violated; the smallest item of all is now at the top of the tree. It is going to have to make its way down the tree until the heap condition is restored. This process is known as sinking to the bottom.

Sinking is the process of repeatedly exchanging an item with the larger of its children until the heap condition is restored or the bottom of the tree is reached. In this example, the larger of the children of the sinking item is P, so the A is exchanged with it. Figure 8-14 shows the state of the heap after this first exchange is made.

X

P

A K

E M F D

D B

Figure 8-14: The top element has been sunk down one level.

The heap condition is still violated because the A is larger than both of its children. The larger of the children is M, so the swap is made with that item. Figure 8-15 shows the state of the heap after this exchange is made.

190

Priority Queues

X

P

M K

E A F D

D B

Figure 8-15: The heap condition is restored after sinking.

The heap condition has been restored and the largest item is removed, leaving the heap one item smaller than it was. Armed with your new understanding, you can now use this concept to implement a priority queue.

In the next Try It Out, you test and implement a priority queue that stores the elements in the queue in a heap-ordered list — that is, a list arranged logically as a heap. This is the most complex of the three implementations covered in this chapter.

Try It Out

Testing and Implementing a Heap-ordered Priority Queue

First create a test case that is specific to your heap-ordered implementation, as shown here:

public class HeapOrderedListPriorityQueueTest extends AbstractPriorityQueueTestCase

{

protected Queue createQueue(Comparator comparator) {

return new HeapOrderedListPriorityQueue(comparator);

}

}

You structure the implementation just as you did with the other two priority queues, with a list to hold the items and a Comparator to order them appropriately:

public class HeapOrderedListPriorityQueue implements Queue { private final List _list;

private final Comparator _comparator;

public HeapOrderedListPriorityQueue(Comparator comparator) { assert comparator != null : “comparator cannot be null”; _comparator = comparator;

_list = new ArrayList();

}

...

}

191

Chapter 8

You create the enqueue() method to add the new item to the underlying list and then swim it up the heap:

public void enqueue(Object value) { _list.add(value);

swim(_list.size() - 1);

}

You create the swim() method, which accepts a parameter that is the index of the item that is swimming up the heap. You compare it with its parent (if it has one), swapping them if the parent is smaller. You call swim() recursively to continue the process further up the heap:

private void swim(int index) { if (index == 0) {

return;

}

int parent = (index - 1) / 2;

if (_comparator.compare(_list.get(index), _list.get(parent)) > 0) { swap(index, parent);

swim(parent);

}

}

You have seen numerous swap() methods before, so this should cause you no trouble:

private void swap(int index1, int index2) { Object temp = _list.get(index1); _list.set(index1, _list.get(index2)); _list.set(index2, temp);

}

Next you create the dequeue() method. That returns the item at the front of the list. You then swap the item at the end of the list to the front of the list, and sink it down through the heap to restore the heap condition:

public Object dequeue() throws EmptyQueueException { if (isEmpty()) {

throw new EmptyQueueException();

}

Object result = _list.get(0); if (_list.size() > 1) {

_list.set(0, _list.get(_list.size() - 1)); sink(0);

}

_list.delete(_list.size() - 1); return result;

}

192

Priority Queues

Create the sink() method that is used to swap the item with the largest of its children. Be careful to cater to cases in which the item has two, one, or no children at all:

private void sink(int index) { int left = index * 2 + 1; int right = index * 2 + 2;

if (left >= _list.size()) { return;

}

int largestChild = left; if (right < _list.size()) {

if (_comparator.compare(_list.get(left), _list.get(right)) < 0) { largestChild = right;

}

}

if (_comparator.compare(_list.get(index), _list.get(largestChild)) < 0) { swap(index, largestChild);

sink(largestChild);

}

}

You’ll be exhausted after looking at that bit of code, so the good news is that the remaining methods are as simple as can be:

public void clear() { _list.clear();

}

public int size() { return _list.size();

}

public boolean isEmpty() { return _list.isEmpty();

}

How It Works

The enqueue() method is simple because it passes most of the hard work off to the swim() method after adding the new item to the underlying list. The parameter passed to the swim() method is the index of the item that needs to swim up the heap. The swim() method has the task of comparing the item at the index provided with its parent item in the heap, and exchanging it if the item is larger than its parent. If an exchange is required, the method calls itself recursively to continue the process higher up the heap. The method stops when the index is 0, as this means we are at the top of the heap. Notice also that the formula used to identify the index of the parent element matches the explanation given earlier in the chapter.

193