Г.В. Алексеевская Использование графиков при решении задач, уравнений, неравенств и систем

10

21. При каких значениях a уравнение

2x −4

= ax −1

у

имеет два решения?

Введем обозначения у1=2 х-2 ; у2=ах–1. По-

у1

строим график функции y1 (рис.

26). Очевидно, что

график функции у2 должен располагаться в растворе

угла. Полагая, что график у2 совпадает с одним из лу-

х

чей угла; при a =1/2 и a =2 имеем одну точку пересе-

Рис. 26

чения.

Ответ: 1/2<a<2.

22. При каких значениях a уравнение

x2 −5x +6

= ax имеет три решения?

Введем

обозначения:

y

=

x2 −5x +6

;

1

y2 = ax .

у1

На

рис.27

представлен

график

функции:

у2

y =

(x −5 / 2)2

−1 / 4

2). График функции

y

= ax

1

2

х

– прямая с угловым коэффициентом

a >0 (т.к. при

Рис. 27.

a <0 –

решений

нет), проходящая через

начало

координат, с графиком функции y2 имеет три точки пересечения лишь в том случае, когда касается участка графика, заключенного в промежутке (2, 3), т.е. имеет одну точку пересечения с параболой y3 = −(x −5 / 2)2 +1 / 4 . Решаем уравнение

y

2

= y ; ax = −x2

+5x −6 ;

квадратное

уравнение x2

−5x + ax +6 =0

имеет

3

0=(а-5)2–24;

одно

решение,

если

дискриминант

равен

нулю:

a2 −10a + 25 −24 =0 ;

a2 −10a +1 =0 ;

a1,2

= 5 ±

25 −1 = 5 ± 24 = 5 +

;

5 −

.

24

24

При a1 = 5 +

>1;

y2 = ax пересечет y1 в двух точках,

24

следовательно,

это значение а не подходит.

Ответ: a = 5 − 2 6 .

23.

При

каких

значениях

k

уравнение:

у

С

E

x

−3

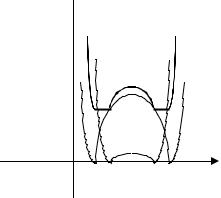
= k(x −9) имеет 1, 2, 3, 4 решения?

A

D

Введем обозначения:

B

y1 =

x

−3

; y2 = k(x −9).Построим график функции

-3

3

х

y1 (рис. 28). График функции y2 – прямая, смещенная

Рис. 28

11

по оси ОХ на 9 вправо с угловым коэффициентом k . Очевидно, если k =1, то прямая параллельна участку DЕ, т.е. y1 и y2 не пересекаются и решений уравнение не имеет. При k =0, y2 =0 уравнение имеет два решения х=±3. В промежутке 0 < k ≤1 решений также нет. Поскольку k =tg α, α - угол наклона прямой, то, увеличивая α до π/2, будем иметь одно решение; пересечение графика y2 с графиком y1 на уча-

стке DЕ, т.е. 1 < k < ∞. x находим из решения уравнения: (х–3)=kх–9; х(1-k)=3(1– 3k); х1=3(1–3k)/(1– k).

Рассмотрим отрицательные значения k: если прямая у2 проходит через точку С (0, 3), то уравнение имеет три решения. Найдем это значение k. Подставим координаты (0, 3) в выражение у2=k(х-9), будем иметь 3=k (0-9); k=-1/3, т. е. при k=-1/3 х1=3(1–3k)/(1–k); х2=0. х3 найдем как точку пересечения у2 с участком графи-

ка y1 АВ: у=-(х+3), т.е. -х-3=k(х-9); -х(1+k)=3(1–3k); х3=-3(1–3k)/(1+k). При -

1/3<k<0 уравнение имеет четыре решения: х1=3; х2 найдем как точку пересечения у2

с участком графика у1 СD: у =-(х-3); -х+3=k(х-9); х(1+k)=3(1+3k);

х2=3(1+3k)/(1+k). х3 находим как точку пересечения графика у1 с участком ВС:

у=х+3, т.е. х+3=k(х-9); х (1-k)=-3(1+3k); х3=-3(1+3k)/(1–k). х4 находим как точку пе-

ресечения графика у1 с участком АВ: х4=-3(1–3k)/(1+k). При k<-1/3 уравнение имеет два решения: х1=3(1–3к)/(1–к); х2=-3(1–3к)/(1+к).

Ответ: х1=3(1–3k)/(1–k) при 1<k<0;

х1=3; х2=-3 при k=0;

х1=3(1–3k)/(1–k); х2=-3(1–3k)/(1+k) при k<-1/3; х1=3(1–3k)/(1–k); х2=0; х3=-3(1–3k)/(1+k) при k=-1/3;

х1=3(1–3k)/(1–k); х2=3(1+3k)/(1+k); х3=3(1+3k)/(1–k);х4=-3(1–3k)/(1+k) при –1/3 < k < 0.

24.Найти число решений уравнения

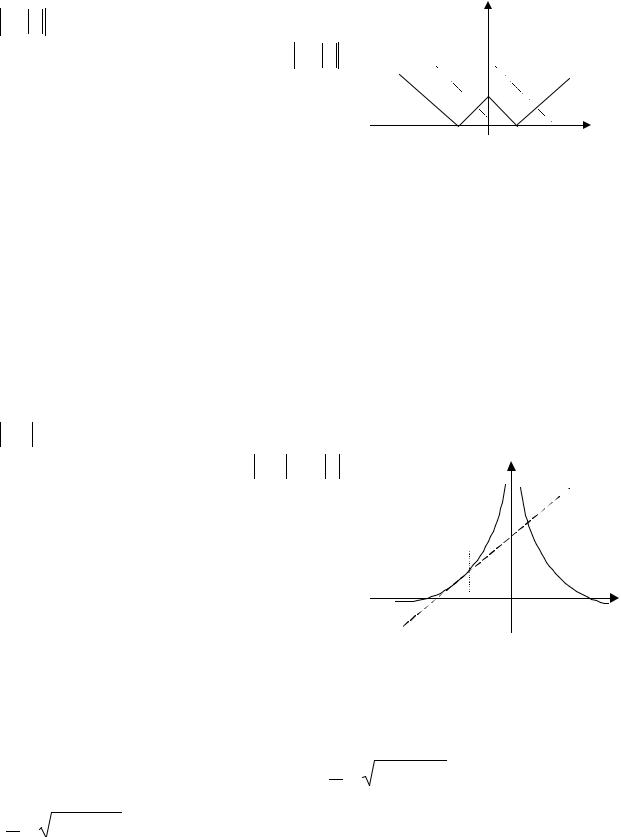
х2-6х+8 + х2–6х+5 =а.

Введем обозначения:

у1= х2-6х+8 = (х–3)2–1 ; у2= х2-6х+5 = (х-3)2–4 ; у3=у1+у2; у4=а.

График у3 построен аналогично №7, (рис. 29). Поскольку а=const, график у4 – прямая, параллельная оси ОХ.

Ответ: a <3 – решений нет;

при a =3 1 < x < 2 и 4 < x <5 ;

при 3 < a <5 – четыре решения; при a =5 – три решения;

при a >5 – два решения.

у

у3

у2

у1

х

Рис. 29

12

25.

Для любого a решить неравенство:

у

1− x < a − x .

Введем

обозначения

y1 = 1− x ;

А

у2

у1

y2 = a − x .

График функции

y1 представлен на

С

Е

рис.30. График функции y2 – прямая, проходящая

через точку (а, 0) с угловым коэффициентом (-1),

В

D

х

т.е. параллельная участку АВ, графика функции

Рис. 30

y1 . Поэтому

при a ≤ −1 неравенство решений не

имеет; при −1 < a ≤1

x < x1.

x1 найдем как точку пересечения у2 с участком гра-

фика у1 ВС:

y = x +1,

т.е. x +1 = a − x ;

2x = a −1;

x1 =(a −1) / 2.

При a > 0

x < x2 . x2 найдем как точку пересечения

у2 с участком графика y1 DЕ: y = x −1,

т.е. x −1 = a − x ; 2x = a +1; x2 = (a +1) / 2 .

Ответ: при a ≤ −1 – решений нет;

при −1 < a ≤1

x < (a −1) / 2;

приa > 0

x < (a +1) / 2.

26. Для любого a решить неравенство:

1/ x < a + x .

Введем

обозначение:

y1 = 1/ x =1/ x ;

у

y2 = a + x (рис. 31). График функции у2 – прямая,

у2

проходящая через точку (0, а) с угловым коэффи-

циентом 1. На рис. 31 показано положение графи-

ка функции у1, когда прямая касается левой ветви

у1

гиперболы

y = −1/ x ,

т.е.

уравнение

−1/ x = a + x

имеет

одно

решение:

х2

х1

х

ax + x2 +1 = 0 или x2 + ax +1 =0 . Приравняем

Рис. 31.

дискриминант

этого квадратного уравнения к ну-

лю: a2 −4 = 0 ; a2 = 4 ; a = ±2 , так как рассматриваем левую ветвь гиперболы, то

a = 2. Таким образом,

при a ≤ 2 неравенство справедливо для x > x1;

x1 найдем

как точку пересечения функции y2

с правой веткой гиперболы:

y =1/ x ( x > 0 ),

т.е.

1/ x = a + x ;

x2 +ax −1 = 0 ;

x = −a ± a2

/ 4 +1,

т.к.

x > 0 ,

то

1,2

2

x = −a +

a2

/ 4 +1. При a > 2 x > x и x < x < x

2

;

x

2

,

x

найдем как точки

1

2

1

3

3

13

пересечения

у2

с

левой

веткой

гиперболы

( x2 ,x3 <0 )

y = −1 / x ,

т.е. −1 / x = a + x ; x2 + ax +1 =0 ; x ,x = −a2 / 2 ±

a2 / 4 −1

.

2

3

Ответ:

a ≤ 2

x > −a / 2 +

a2 / 4 +1

;

a > 2

x > −a / 2 +

a2 / 4 +1

;

a / 2 −

a2 / 4 −1

< x < −a / 2 +

a2 / 4 −1

.

27. При

каких

действительных

a

множество

y

<1−ax2 является подмножеством 2х + у <5/4?

Рассмотрим

первое

неравенство:

линией

у2

y

=1−ax2

плоскость

разбивается

на

внутреннюю

часть и внешнюю. Построим эту линию. Заметим, что

линия симметрична относительно ОХ и ОУ. При y > 0

имеем y =1−ax2 – это парабола с вершиной в точке (0,

х

у1

1) параметром ( −a / 2 ), т.е. ветвями вниз (рис. 32).

Чтобы определить, какая часть плоскости, разде-

ленная параболой, удовлетворяет неравенству,

подста-

вим координаты точки (0, 0), лежащей во внутренней

Рис. 32

области, в неравенство, получим 0<1. Неравенство спра-

ведливо. Значит, координаты внутренних точек удовлетворяют неравенству (заштрихованная область на рис. 32), отобразим построенную область симметрично на

область y <0 . Ось ОХ парабола пересекает в точках±1 a .

Рассмотрим второе неравенство. Построение графика функции 2х + у =5/4 аналогично №4, т.е. это ромб с вершинами (0, ±5/4), (±5/8, 0). Координаты точек, лежащих внутри ромба, удовлетворяют второму неравенству.

Чтобы ответить на поставленную задачу, нужно определить значение параметра а, при которых заштрихованная фигура лежит внутри ромба. Поскольку фигура симметрична относительно оси ОХ, задача тождественна тому, что нужно найти значения а, при которых парабола лежит внутри ромба.

Найдем значение а, при котором правая ветвь параболы у=1–ах2 не пересекает прямую у=-2х+5/4, т.е.уравнение 1–ах2=-2х+5/4 не имеет решение ах2–2х+1/4= 0. Дискриминант сравним с нулем: 1–а/4<0, при а>4, решений нет.

Ответ: а > 4.

14

x + 3		y		+ 5 =0;
28. При каких значениях a система имеет три решения:	2					2
					+ y		= 4.
( x −a )

Построим	график функции	у =-(5+х)/3 –			у
симметричный относительно оси ОХ, т.е. достаточ-
но построить для у>0: у=-1/3(х+5) и отобразить на
область у < 0 (рис. 33).
Линия,	определяемая	уравнением
( x −a )2 + y2 = 4 – это окружность с центром в			-5			х
точке (а, 0) радиуса 2. Окружность будет иметь три				Рис. 33
точки пересечения с графиком первой функции, ес-

ли она проходит через точку (-5, 0), т.е. центр окружности должен находиться в точ-

ке (-7, 0).

Ответ: a = −7 .

2

+ y = 2x + a;

x

имеет решение?

29. При каких значениях a система

2

2

+ y

= 2x;

x

Преобразуем систему:

выделим полный квад-

у

2

− 2x

+1

−1 − a = −y;

рат

по

x :

x

2

2

− 2x

+1

−1 + y

=0.

x

2

=1 + a − y;

( x −1 )

2

2

х

+ y

=1

( x −1 )

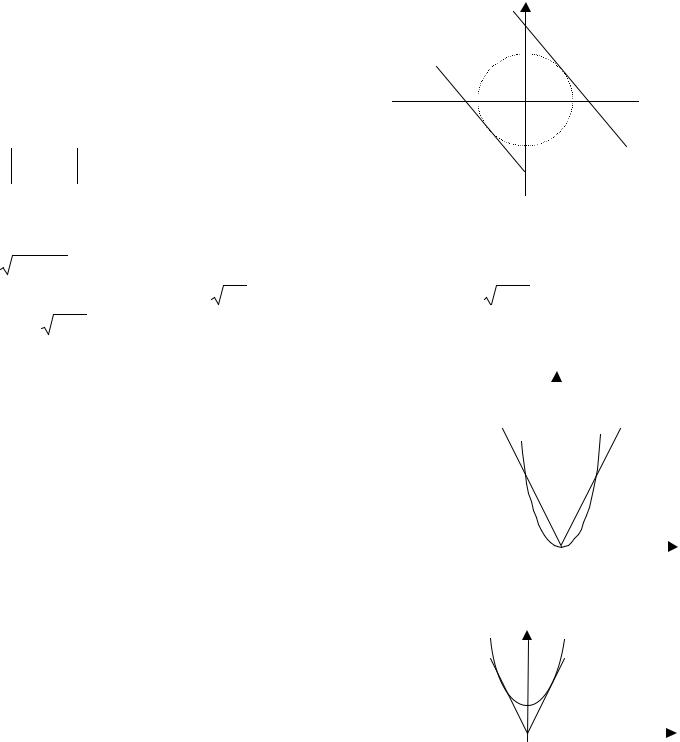
Первое уравнение определяет параболу с вершиной в

точке (1, 1+а), параметром

– 1/2, т.к. (х-1)2≥0, то

Рис. 34

1 + a − y ≥0 , т.е.

y ≤1 + a . Второе –

окружность с

центром в точке (1, 0), радиуса 1 (рис. 34).

Парабола может не касаться окружности, тогда решений система не имеет; касаться ветвями или пересекать – тогда два решения; касаться вершиной – тогда три решения или одно, и если ветви параболы дважды пересекают окружность, тогда четыре решения. Парабола у=-(х-1)2+1+а касается вершиной окружности при a =0 и a = −2 ; при − 2 < a <0 пересекает окружность в двух точках. Для рассмотрения остальных случаев вычтем из второго уравнения первое, получим квадратное урав-

нение y2 − y + a =0 . Если дискриминант Д=0, то парабола касается ветвями ок-

ружности; если Д<0 – не касается окружности; Д>0 – каждая ветвь дважды пересекает окружность. Д=1/4-а.

Ответ: а<-2; а>1/4 - решений нет; а=-2 – одно решение; -2<a<0, а=1/4 – два решения; а=0 – три решения; 0<a<1/4 – четыре решения.

15

30. При

каких значениях а система

у

2

+ y

2

= 2( 1 + a );

x

2

имеет два решения?

=14;

( x

+ y )

Запишем тождественную

систему:

х

2

+ y

2

= 2a + 2;

x

+ y2

=14.

x2

График

функции

х+у =14

– две прямые:

Рис. 35.

у=14–х; у=-14–х (рис. 35).

График функции,

описываемой первым уравнением, - окружность с центром в точке (0, 0), радиуса

2a + 2 . Очевидно, для х>0 окружность должна касаться прямой у=14–х. То есть

уравнение

x2 +14 −2

14x + x2 = 2a + 2 ;

2x2 −2

14x +12 −2a =0 ;

x2 −

14x +6 − a =0 имеет

одно решение

(дискриминант

Д=0).

14–24+4а;

4а=10; а=5/2.

Ответ: а = 5/2.

	31. Сколько решений имеет уравнение		у
	2 х -х2=а для любых а≥0?			у1
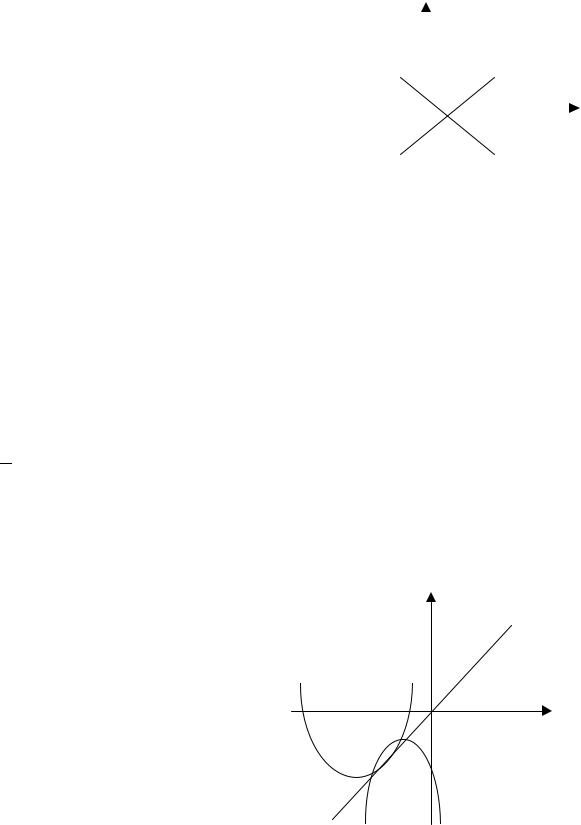
	Найдем область допустимых значений: 2 х≥ х2 –
	решим неравенство графически: у1=2 х ; у2=х2 (рис.
	36). График функции у1 лежит выше графика функции у2
				у2
	на участке –2≤х≤2. Возведем обе части уравнения в
	квадрат, будем иметь: 2 х -х2=а2. Решаем его графиче-
	ски: у1=2 х ; у2=х2+а2 (рис. 37). График функции у2 –					х
	парабола, смещенная на а2 вверх. Если парабола касает-	Рис. 36
	ся графика у1, то уравнение имеет два решения, что то-
	ждественно задаче: при каких значениях а уравнение
	имеет единственное решение: 2х=х2+а2;х2–2х+а2=0.		у1
	Приравняем дискриминант Д к нулю: 1–а2=0; а=±1, с

учетом условия (а≥0) а=1.

Ответ: а=0–уравнение имеет три решения; 0<a<1–

четыре решения; а=1–два решения.		х
32. Для любых значений а решить уравнение:	Рис. 37

2–а-х + х–а-4 =9.

Построим график в плоскости АОХ аналогично построению в №5 (ось ОУ заменим осью ОА), получим смещенный квадрат с диагоналями а=2–х; а=х–4, которые являются осями симметрии, (рис. 38). Этими прямыми плоскость АОХ раз-

16

бивается на четыре области: верхняя: а>х–4; а>2–х; в				а
этой области уравнение: а–2+х–х+а+4=9;	2а=7;
а=7/2, нижняя: а<х–4; а<2–х здесь имеем уравнение:
2–а–х+х–а–4=9; -2а=11; а=-11/2.
Чтобы найти, как меняется при этом х, найдем
точки пересечения диагоналей квадрата с а=7/2, т.е.						х
х1=7/2+4; х2=2–7/2=-3/2.
Ответ: а=-11/2; а=7/2; -3/2≤х≤15/2; -11/2<a<7/2;
х=-3/2, х=15/2.			Рис. 38

33. В зависимости от значений параметра a определить число корней уравнения:

х2+4х-2 х-а +2-а=0.

На плоскости (х; а) строим прямую х-а=0, которая разобьет плоскость на две области. В I области уравнение принимает вид: а1=-(х+1)2-1 – парабола с вершиной (-1, -1). Во второй области уравнение принимает вид: а2=1/3(х2+6х+2)=1/3(х+3)2-7/3-парабола с вершиной в (-3, -7/3). Точки пересечения парабол лежат на прямой а=х, т.е. х=-1, -2.

Ответ:

если а (-∞; -7/3) (-2; +∞) два корня, если a = 73 и a = −2 три корня,

если a ( 73 ;−2 ) четыре корня,

если а<-7/3; а>-2 уравнение имеет два корня, если а=-7/3; а=-2 – три корня,

если –7/3<a<-2 – четыре корня.

34. При каких значениях p площадь фигуры:2х+у + х–у+3≤р будет равна 24?

Очевидно, р≥0. Построение линии:

	2x + y			+		x − y + 3			= p аналогично №5: ли-
нии		y = −2x ; y = x + 3 (рис. 39), плоскость
ХОУ				разбивают					на	четыре	области:
	y > x + 3 ;						y > −2x верхняя, в этой области
запишем							уравнение 2х+у–х+у–3=р; х+2у–
3=р; нижняя y < x + 3 ;										y < −2x , уравнение
в		этой					области:			-2х+у+х–у+3=р;
− x −2 y +3 = p . Эти										прямые параллельны.
Левая область								задается неравенствами
	y < x + 3 ;						y < −2x ,			уравнение	в этой

а	II	а=х
		I
а2		х
	а1
Рис. 39

17

области имеет вид: 2x + y + x − y + 3 = p ; 3x + 3 = p ;

у

x = 3p −1, эти линии параллельны оси ОУ. Таким обра-

зом, полученная фигура параллелограмм. Площадь параллелограмма находится как произведение основания на вы-

соту. Высота – это расстояние между прямыми x =	p	−1,		х
	3

	х=-р/3–1, симметрично расположенными относительно	Рис. 40
	прямой х=-1, т.е. расстояние между ними 2р/3.
	Чтобы найти длину основания, найдем точки пересечения прямой х=р/3–1 с

прямыми у=х+3; к=-2х, т.е. у1=р/3–1+3=р/3+2; у2=-2р/3+2. Расстояние между этими точками d = у1–у2 =р/3+2+2/3р–2=р. Тогда из условия, площадь фигуры равна 24, 2/3р2=24; р2 = (24× 3)/2=36, с учетом, что р≥0.

Ответ: р=6.

35. Решить неравенство log(а2+ х2) / 2 х ≥ 1. Область допустимых значений х>0. Рассмотрим два случая:

a2	+ x2		<1;
	2
a )
		a2 + x2
x ≤				;
	2

Выделяя полный квадрат по х получим:

a2	+ x2		>1;
	2
б)
		a2 + x2
x ≥				.
	2

	2	+ a	2	< 2;		2	+ a	2	> 2;
x					x
a )			2		б)			2
				+ a ≥1;					+ a ≤1.
( x −1 )					( x −1 )

Построим эти множества на плоскости ХОА с учетом того, что х>0 соответственно (рис. 41, а) и (рис. 41, б).

у		у
	а=const		a=const
х1	х	х2	х3 х

Рис. 41, а

Рис. 41, б

18

Чтобы найти область изменения х для различных а, положим а=const и

найдем x

= − 1 −a2 +1, x =

2 −a2

, x = 1 −a2

+1.

1

2

3

Ответ:

1< a <2,

0 < x <

2 − a2

;

a <1, 0 < x <1 −

1 −a2

или

у

2 − a2 < x <1 +

1 − a2 , a≥2 решений нет.

36. При каких значениях a уравнение 32х3+ах+1=0 имеет три действительных корня?

Введем обозначение: у1=32х3+1; у2=-ах. График функции у1 представлен на рис. 42, а.

Очевидно, что прямая у2=-ах проходит через точку (0, 0), в первой и третьей четверти, т.е.

–а>0, (а<0).

Рассмотрим случай, когда прямая у2 касается кубической параболы в первой четверти, т.е. имеем две точки пересечения, тогда: 32х3+ах+1=32(х-х1)2(х–х2). Приравниваем коэффициенты при одинаковых степенях х:

32(х3–2х2х1+2хх1х2+хх12–х12х2–х2х2)=32х3+ах+1

у

х

Рис. 42, а.

−2x1 − x2 =0;			x2 = 2x1;
32( 2x x		+ x 2 ) = a;	32x		2 × x =1;
	1 2	1		1	1
		=1;		=	3 1 / 64 =1 / 4; x2 = −1 / 2.
−32x12 x2			x1

a = 32 ( −2 1 / 4 1 / 2 +1 / 16 ) = −8 + 2 = −6 .

Поскольку (-а) = tgα, где α - угол наклона прямой у2 к оси ОХ.
Ответ: -∞<a<-6.								у
Предлагаем второй способ решения этого
примера.								1
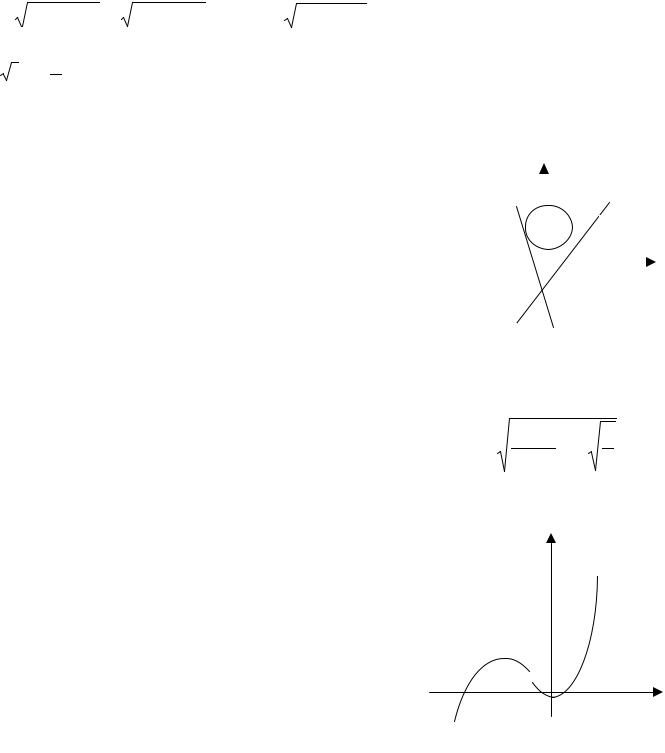
С учетом того, что коэффициент при х3: 32>0,
изобразим	схематично,	кубическую параболу
у=32х3+ах+1 (рис. 42, б), парабола пересекает ось ОХ									х
в трех точках, ось ОY в точке (0; 1).
Найдем	критические	точки		функции	у:		Рис. 42, б
у'=96х2+а; 96х2+а=0; x = ±			.	Очевидно,	что
		−a / 96

a <0 . При x = −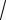−a / 96 y принимает максимальное значение: y( − −a / 96 ) = −31 −a3 / 96 −a −a / 96 +1, т.к. уmax>0, а<0,

19

получаем неравенство:

1

−a3 / 96 + −a3 / 96 > −1;

2

−a3 / 96 > −1; введем замену: t = −a3 / 96 ;

3

9

3

t > −3 ;t >

; -а3/96>9/4; a3

< −216 .

4

2

Ответ: а<-6.

37. При каких значениях a система

( x +3 y ) /( x − y ) ≥0;

имеет хотя бы

у

y( y −8 ) + x2 ≤( a −4 )( a

у=-1/3х

+4 );

у=х

одно решение?

На рис. 43 заштрихованная область соответству-

ет множеству точек первого неравенства, т.к. взяв точ-

х

ку (1; 0) и

подставив в неравенство, констатируем,

что оно справедливо, далее области

чередуются. Точ-

Рис. 43

ки, удовлетворяющие неравенству – это точки, лежа-

щие внутри окружности:

(у-4)2+х2=а2 с центром в точке (0, 4), радиуса а. Если окружность касается прямой у=-1/3х, то решение существует: у2–8у+16+9у2=а2; 10у2–8у+16–а2=0. Дискриминант

Д приравняем к нулю: Д=16–10×16+10а2=0; 10a2 =9 16; a =	9 16	=6	2 .
	10		5

Ответ: а≥6√2/5.

38. Найти значение а, при которых уравнения

log1/4х2+log1/4 (х+3)=а и log1/4х+log1/10 (х+3)=а/2 равно-

сильны. Найдем область допустимых значений: первого уравнения х>-3, второго х>0, перепишем урав-

нение в тождественной форме: log1/4 х2 (х+3) = а, т.е. (1/4)а=х2(х+3).

Учитывая область допустимых значений, построим график (рис. 44) у1=х2(х+3)–это кубическая парабола, пересекающая ось ОХ в точках (0, -3).

Найдем экстремумы у1: х(2х+6+х)=0; х=0; x = −2 ; у1 (-2)=4. Поскольку у2 – прямая, то эти уравнения равносильны, если прямая лежит выше

у=4, т.е. (1/4)а>4; 4−a > 4 .

Ответ: a < −1.

у

х

Рис. 44