Т.С. Жирнова Дифференциальные уравнения

10

d

2

z

2

является y. В этом случае y′′ = z

dz

;

y

′′′

= z z

dz

;

и т.д. При

dy

dy

2

+

dy

подстановке производных порядок уравнения понизится на единицу. Пример 1. Решить уравнение y′′′ = 60x2 .

Решение. Умножая обе части данного уравнения 3-го порядка на dx и затем интегрируя, получаем уравнение 2-го порядка: y′′′dx = 60x2 dx; y′′ = 20x3 + c1. Далее тем же способом получаем уравнение 1-го порядка, а затем искомую функцию – общий интеграл данного

уравнения:

′′

3

dx + c1dx;

y

′

= 5x

4

+ c1 x + c2 ;

y dx

= 20x

y = x

5

+c

x2

+ c

x + c

.

2

1

2

3

Пример 2. Решить уравнение

(x −3) y′′+ y′ = 0.

Решение. Данное уравнение не содержит явно y. Полагая y′ = z(x),

получим

y

′′ =

dz

;

при этом исходное уравнение обращается в уравне-

dx

dz

ние первого порядка:

(x −3)

+ z = 0.

dx

dz

dx

Разделяя переменные и интегрируя, найдём

= −

;

z

x −

3

ln

z

= −ln

x −3

+ln c;

z(x −3)

= c;

z(x −3) = ±c = c1.

Заменяя z через

dy

,

получим уравнение (x −3)

dy

= c1 , решая ко-

dx

dx

торое, найдём искомый общий интеграл:

Пример 3. Решить задачу Коши: y′(0) = 2.

	dy =	c1dx	;	y = c1 ln		x −3		+c2 .
		x −3
	yy′′−(y′)2			= 0;		y(0) = 1;

Решение. Данное

уравнение

не содержит явно x.

Полагая

y′ = z( y) ,

получим

y′′ =

dz

z. После данной подстановки

уравнение

dy

примет вид: yz

dz

− z 2 = 0 .

Сократим на z и разделим переменные:

dy

dz

=

dy

;

ln

z

= ln

y

+ln c;

z = ±cy

или z = c1 y .

z

y

11

Подставляя вместо z

dy

и

разделяя переменные, имеем

dx

dy

= c1 y;

dy

= c1dx;

ln

y

= c1 x +ln c2 ;

потенцируя, получим общий ин-

dx

y

y

= c2ec1x

или

y = c3ec1x .

теграл уравнения:

Заметим, что для данного уравнения решением является также функция y ≡ 0 , но это решение не удовлетворяет начальным условиям.

Используя начальные условия, находим c3 = 1, c1 = 2, т.е. частным решением исходной задачи Коши будет функция y = e2 x .

2.2.Линейные однородные уравнения

спостоянными коэффициентами

Линейным однородным уравнением называется уравнение

y(n) + p1 y(n−1) + p2 y(n−2) +... + pn−1 y′+ pn y = 0,

(2.4)

все члены которого первой степени относительно функции и её производных, а коэффициенты p1, p2,…, pn – известные функции от аргумента х или постоянные.

Общий интеграл однородного линейного уравнения n-го порядка

(2.4) имеет вид y = c1 y1 +c2 y2 +... +cn yn , (2.5)

где y1, y2,…, yn - линейно независимые частные интегралы этого уравнения.

Если все коэффициенты pi однородного линейного уравнения (2.4) постоянны, то его общий интеграл находится с помощью характеристического уравнения

r n + p1r n−1 + p2 r n−2 +... + pn−1r + pn = 0,

(2.6)

которое получается из исходного уравнения, если сохраняя в нём все коэффициенты pi , заменить функцию y единицей, а все её производные соответствующими степенями r. При этом:

1)если все корни r1, r2,…, rn характеристического уравнения (2.6) действительны и различны, то общий интеграл уравнения (2.4)

выражается формулой

y = c1er1x + c2 er2 x +... + cn ern x ;

2)если характеристическое уравнение имеет пару однократных комплексных сопряжённых корней r1,2 =α ± βi , то в формуле (2.5) соответствующая пара членов заменяется слагаемым

eαx (c1 cos βx +c2 sin βx);

12

3)если действительный корень r1 уравнения (2.6) имеет кратность k, (r1 = r2 = … = rk), то соответствующие k членов в формуле (2.5)

заменяются слагаемым

er1x (c1 + c2 x + c3 x2 +... + ck xk −1 );

4)если пара комплексных сопряжённых корней r1,2 =α ± βi уравнения (2.6) имеет кратность k, то соответствующие k пар членов в формуле (2.5) заменяются слагаемым

eαx [(c1 + c2 x +... + ck x k −1 )cos βx + (ck +1 + ck +2 x +... + c2k x k −1 )sin βx]. .

Пример 1. Решить уравнение: y′′− 2 y′−3y = 0 .

Решение. Заменяя в данном дифференциальном уравнении функцию y единицей, а её производные соответствующими степенями r, напишем его характеристическое уравнение: r 2 − 2r −3 = 0.

Корни этого уравнения r1 = -1, r2 = 3 действительны и различны, поэтому согласно правилу 1 искомый общий интеграл данного уравне-

ния будет y = c1e−x + c2 e3x .

Пример 2. Решить уравнение: y′′′− 6 y′′+13y′ = 0.

Решение. По указанному правилу составляем характеристическое уравнение: r3 – 6r2 + 13r = 0. Оно имеет один действительный корень

r1 =0 и пару комплексных сопряжённых корней r2,3 = 3	±	2i. Согласно
правилам 1 и 2 общий интеграл данного уравнения
y = c1 + e3x (c2 cos 2x + c3 sin 2x) .
Пример 3. Решить уравнение: y′′+ 4 y′+ 4 y = 0 .	r2
Решение. Написав характеристическое уравнение		+ 4r + 4 = 0,

находим, что оно имеет равные действительные корни r1 = r2 = -2. Со-

гласно	правилу 3, общий		интеграл исходного уравнения
y = e−2 x (c	+c	x).
1	2		y(7 ) + 2 y(5) + y(3) = 0.
Пример 4. Решить уравнение:

Решение. Данному уравнению соответствует характеристическое уравнение: r7 + 2r5 + r3 = 0 или r3 (r2 + 1)2 = 0. Оно имеет трёхкратный действительный корень r = 0 и пару двукратных мнимых сопряжённых корней r = ± i. Согласно правилам 3 и 4, общий интеграл этого уравне-

ния	y = c1 + c2 x + c3 x2 + (c4 + c5 x) cos x + (c6 + c7 x) sin x.

Если известны линейно независимые частные решения y1(x), y2(x), …, yn(x) линейного однородного дифференциального уравнения (2.4), то вместе с общим решением y этого уравнения они образуют линейно зависимую систему, и поэтому следующий определитель (n + 1)-го порядка равен нулю:

y y1 y′ y1′ y′′ y1′′

L L

y(n) y1(n)

13

y2 L yn

y2′ L yn′

y2′′ L yn′′ = 0.

L L L

y2(n) L yn(n)

Раскрывая данный определитель, получим линейное однородное дифференциальное уравнение, частными решениями которого являются функции y1(x), y2(x), …, yn(x).

Если коэффициенты линейного однородного уравнения (2.4) постоянны, то такое уравнение можно восстановить, получая соответствующее характеристическое уравнение. Корни характеристического уравнения берутся из вида заданных частных решений дифференциального уравнения.

Пример 5. Построить линейное однородное уравнение, для которого функции y1(x) = ex, y2(x) = sinx, y3(x) = cosx образуют фундаментальную систему решений.

Решение. Искомое уравнение имеет вид

y		ex		sin x	cos x
y	′	e	x	cos x	−sin x	= 0.
y′′		ex		−sin x	−cos x
y′′′		ex		−cos x	sin x

Разложив определитель по элементам первого столбца, получим

ex

cos x

−sin x

− y′

ex

sin x

cos x

+ y′′

ex

sin x

cos x

y

ex

−sin x

−cos x

ex

−sin x

−cos x

ex

cos x

−sin x

−

ex

−cos x

sin x

ex

−cos x

sin x

ex

−cos x

sin x

− y′′′

ex

sin x

cos x

ex

cos x

−sin x

= 0

ex −sin x

−cos x

или −2ex y +2ex y′−2ex y′′+2ex y′′′ = 0 .

Сокращая на 2ex, получаем окончательный вид дифференциального уравнения: y′′′− y′′+ y′− y = 0 .

Данное уравнение можно получить и другим путём, если учесть, что частному решению линейного однородного уравнения вида y1 = ex соответствует корень характеристического уравнения, равный r1 = 1, а частным решениям y2 = sinx, y3 = cosx соответствует пара мнимых

14

корней характеристического уравнения r1,2 = ± i. Значит, характери-

стическое уравнение имеет вид (r - 1)(r - i)(r + i) = 0; (r – 1)(r2 + 1) = 0

или r3 – r2 + r – 1 = 0, а линейное однородное дифференциальное урав-

нение, соответствующее данному характеристическому уравнению,

имеет вид y′′′− y′′+ y′− y = 0 .

Пример 6. Составить однородное линейное дифференциальное уравнение по следующим его частным решениям: y1 = 1; у2 = x; y3 = e3x.

Решение. Первым двум частным решениям соответствует один двукратный корень характеристического уравнения, равный нулю, т.е.

r1 = r2 = 0. Частному решению y3 = e3x соответствует однократный корень характеристического уравнения r3 = 3. Отсюда следует, что характеристическое уравнение имеет следующий вид r2(r – 3) = 0 или

r3 – 3r2 = 0, а ему соответствует дифференциальное уравнение y′′′−3y′′ = 0 .

2.3.Линейные неоднородные уравнения

спостоянными коэффициентами

Линейным неоднородным уравнением называется уравнение первой степени относительно функции и её производных

y(n ) + p1 y(n−1) + p2 y(n−2) +... + pn−1 y′+ pn y = q(x) ,

(2.7)

отличающееся от линейного однородного уравнения наличием в правой части некоторой функции q от независимой переменной x.

Общий интеграл y линейного неоднородного уравнения равен сумме какого-либо его частного интеграла y и общего интеграла u соответствующего однородного уравнения (получающегося из неоднородного при q = 0 ).

Согласно этому свойству, для решения линейного неоднородного уравнения (2.7) с постоянными коэффициентами pi вначале находят функцию u (по правилам, описанным в п. 2.2), а затем функцию y . Их сумма и даёт общий интеграл y неоднородного уравнения: y = u + y .

Для некоторых специальных видов функции q(x) частный интеграл y можно найти методом неопределённых коэффициентов. По виду правой части q(x) можно заранее указать вид частного интеграла y , где неизвестны лишь числовые коэффициенты, которые определяют при подстановке этого частного интеграла y в исходное неоднородное уравнение.

15

1. Пусть правая часть q(x) = eax Pn (x) , где a - постоянная, в частности, может a = 0; Pn (x) = a0 xn + a1 xn−1 +... + an−1 x + an . В этом случае частное решение y следует искать в виде y = xt eaxQn (x) , где Qn (x) - многочлен той же степени, что и многочлен Pn (x) , но с неизвестными коэф-

фициентами; t – число корней характеристического уравнения, равных a .

2. Если правая часть q(x) = eax [Pn (x) cos bx + Rm (x) sin bx], где Pn (x) и Rm (x) - многочлены соответственно степеней n и m, a и b - постоянные,

то частное решение находим в виде: y = xt eax [QN (x) cos bx + SN (x) sin bx], где QN (x) и SN (x) - многочлены степени N = max(n, m) с неизвестными

коэффициентами; t – число пар корней характеристического уравнения, равных a ±bi .

3. Если правая часть уравнения (2.7) является суммой слагаемых, имеющих вид, рассмотренный в 1. и 2., то частное решение y берём как сумму соответствующих частных решений, определённых в

этих пунктах.

Пример 1. Решить уравнение: y′′+6 y′+5y = 25x2 −2.

Решение. Вначале находим общий интеграл u однородного уравнения y′′+ 6 y′+5y = 0 , соответствующего данному неоднородному уравнению. Его характеристическое уравнение r2 + 6r + 5 = 0 имеет

корни r1 =-5, r2 = -1. Поэтому u = c1e−5 x + c2 e−x .

Далее находим частный интеграл y данного неоднородного уравнения. Для правой части данного уравнения q(x) = 25x2 −2 , согласно указанному правилу (случай 1, число a = 0 и не является корнем характеристического уравнения), y есть функция, подобная q(x), т.е. многочлен второй степени: y = Ax2 + Bx + C.

Отсюда,	дифференцируя, находим y′ = 2 Ax + B, y′′ = 2 A и под-
ставляя y, y′,	y′′ в данное уравнение, получим равенство
2A + 6(2Ax + B) + 5(Ax2 + Bx + C) = 25x2 - 2
или	5Ax2 + (12A + 5B)x + (2A + 6B + 5C) = 25x2 – 2.

Приравнивая коэффициенты уравнения при одинаковых степенях x из обеих его частей, ибо только при этом условии оно будет тождественным, получим систему

5A = 25, 12A + 5B = 0, 2A + 6B + 5C = -2,

из которой находим A = 5, B = -12, C = 12.

16

Следовательно: y = 5x2 −12x +12 , а искомый общий интеграл данного неоднородного уравнения

y = u + y = c1e−5x + c2e−x +5x2 −12x +12 .

Пример 2. Решить уравнение: y′′− 2 y′+10 y = 37 cos 3x .

Решение. Составляем характеристическое уравнение r2 - 2r + 10 = 0, определяем его корни r1,2 =1 ± 3i и находим общий интеграл u однородного уравнения, соответствующего данному неоднородному урав-

нению	u = e x (c1 cos 3x + c2 sin 3x) .
Частный интеграл y		данного неоднородного уравнения, соответ-
ственно его правой части		q(x) = 37 cos 3x (случай 2 при a = 0,
b = 3, числа a ±bi = ±3i не являются корнями характеристического
уравнения), будет иметь вид:			y = Acos3x + Bsin3x.	y′ = -3Asin3x +
Подставляя функцию			y и её производные

3Bcos3x,

y′′ = -9Acos3x – 9Bsin3x в данное неоднородное уравнение, полу-

чим равенство (A – 6B)cos3x + (B + 6A)sin3x = 37cos3x,

которое будет тождеством только при равенстве коэффициентов у подобных членов (y cos3x и y sin3x) в обеих его частях: A – 6B = 37; B + 6A = 0. Решая эту систему, найдём A = 1; B = -6. Следовательно:

y = cos3x – 6sin3x,

= u + y = ex (c1 cos 3x + c2 sin 3x) + cos3x – 6sin3x.

Пример 3. Решить уравнение: y′′−6 y′+9 y = 3x −8ex .

Решение. Написав характеристическое уравнение r2 – 6r + 9 = 0 или (r – 3)2 = 0 и найдя его корни r1 = r2 = 3, получим (по правилу 3 из п. 2.2) общий интеграл соответствующего однородного уравнения

u = e3x (c1 + c2 x) .

Правая часть данного уравнения есть сумма многочлена первой степени 3x и показательной функции -8ex. Поэтому частный интеграл

этого уравнения	y = Ax + B + Cex.
Подставляя y ,	y′= A + Cex, y′′= Cex в данное уравнение

9Ax + (9B – 6A) + 4Cex = 3x – 8ex

и приравнивая коэффициенты у подобных членов из обеих частей полученного равенства, имеем систему: 9A = 3, 9B – 6A = 0, 4C = -8,

1 2

из которой находим A = 3 , B = 9 , C = -2. Следовательно:

			17
y =	1 x +	2	− 2ex , y = u + y = e3x (c1 + c2 x) +	1 x	+	2	−	2ex .
	3	9		3		9
Пример 4. Решить уравнение: y′′′+ y′′ =1				−6x2 e−x .

Решение. Характеристическое уравнение r3 + r2 = 0 имеет корни r1,2 = 0, r3 = -1; общий интеграл соответствующего однородного уравне-

ния u = c1 + c2 x + c3e−x .
Правая	часть данного	уравнения есть	функция	вида
em1x P1 (x) +em2 x P2 (x) , где m1 = 0,		P1(x) = 1, m2 = -1,	P2(x) = -6x2.	При
этом число	m1 есть двукратный корень, а число m2 есть однократный

корень характеристического уравнения. Поэтому частный интеграл данного уравнения y = Ax2 + x(Bx2 +Cx + D)e−x .

Подставляя эту функцию в данное уравнение, получим равенство

2A +[3Bx2 +(2C −12B)x +(6B −4C + D)]e−x =1−6x2e−x ,

откуда имеем систему 2A = 1, 3B = -6, 2C – 12B = 0, 6B – 4C + D = 0,

	из которой найдём	A =		1	,		B = −2,		C = −12, D = −36 .
				2
	Следовательно:	y = 1 x2 − 2x(x2 + 6x +18)e−x ,
				2					+ 1 x2 − 2x(x2 + 6x +18)e−x .
	y = u + y = c		+ c			2	x + c	e−x
		1					3		2

2.4. Метод вариации произвольных постоянных

Этот метод применяется для отыскания частного решения линейного неоднородного уравнения

y(n ) + p1 y(n−1) + p2 y(n−2) +... + pn−1 y′+ pn y = q(x) .	(2.7)
Если известно общее решение (2.5) соответствующего однородно-
го уравнения (2.4), то для определения частного решения	y неоднород-

ного уравнения (2.7) можно воспользоваться методом Лагранжа вариации произвольных постоянных. При этом частное решение неоднородного уравнения находим в том же виде, что и общее решение соответствующего однородного уравнения:

y = c1(x)y1(x) + c2(x)y2(x) + … + cn(x)yn(x),

(2.8)

но произвольные постоянные являются функциями от x. Для получения функций c1(x), c2(x), …, cn(x) имеем следующую систему уравнений

	y	dc1	+ y		dc2	+... + y		dcn	= 0,
		dx		2 dx			n dx
	1

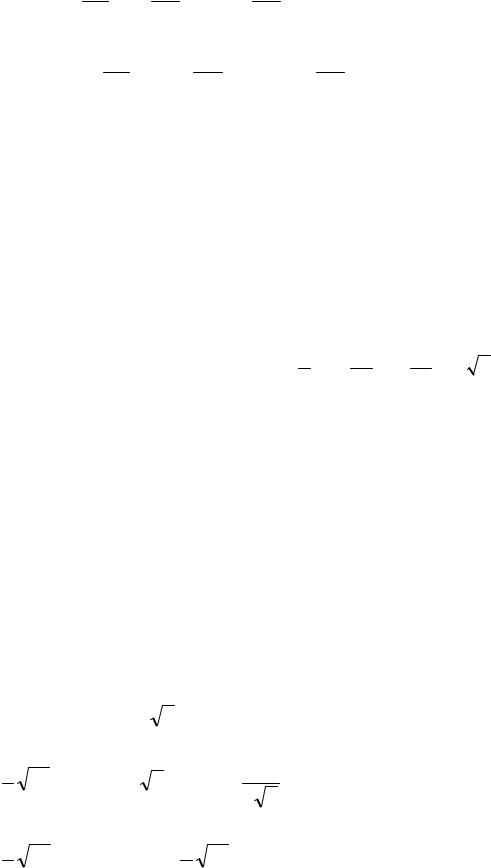
18

y1′ dcdx1 + y2′ dcdx2 +...+ yn′ dcdxn = 0,

………………………………………………

y1(n−1) dcdx1 + y2(n−1) dcdx2 +... + yn (n−1) dcdxn = q(x) .

Определитель этой системы отличен от нуля, так как решения y1, y2,…, yn - линейно независимы, поэтому система имеет единственное

решение относительно	dci	, i =1,2,...,n .
	dx

Проинтегрировав полученные таким образом производные и подставляя их в (2.8), получим частное решение неоднородного уравнения (2.7); общее решение этого уравнения равно сумме полученного частного решения и общего решения соответствующего однородного уравнения.

Пример 1. Применяя метод вариации произвольных постоянных,

найти общее решение уравнения				y′′′− 3 y′′+					62 y′−	63 y = x .
						x			x	x
Решение. Найдём сначала общее решение соответствующего од-
нородного уравнения	y′′′−	3	y′′+		6	y′−	6		y = 0 .
					2		3
		x			x		x

Нетрудно проверить, что функции y1 = x, y2 = x2, y3 = x3 являются частными решениями этого уравнения. Поскольку эти функции линейно независимы, общее решение однородного уравнения имеет вид:

u = c1x + c2x2 + c3x3 , а частное решение исходного неоднородного уравнения, согласно методу вариации произвольных постоянных, нахо-

дим в виде

y = c1(x)x + c2(x)x2 + c3(x)x3. Производные для функций

c1(x), c2(x), c3(x) определяем из системы

′

(x)x

′

2

′

(x)x

3

= 0,

c1

+ c2 (x)x

+ c3

c1′(x) 1 + c2′(x)2x + c3′(x)3x2 = 0,

′

(x) 2

′

(x)6x = x .

c2

+ c3

Решая

эту

систему,

получим

′

(x) =

1

x

3

,

′

(x) = −

′

(x) =

1

.

с1

2

c2

x, c3

x

2

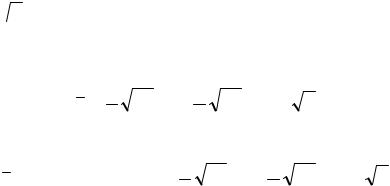
После

интегрирования

получаем

c

(x) = 1 x5

+ c

4

, c

2

(x) = − 2

x3 + c

5

,

1

5

3

19

c3 (x) = x +c6 , где с4, с5, с6 - произвольные постоянные, которые

для данного частного решения могут быть приняты равными нулю. При этом частное решение неоднородного уравнения примет вид:

y = 1	x5 x −	2	x3 x2 + x x3 .
5		3
Следовательно, общее решение исходного уравнения равно
y = u + y = c1 x + c2 x2 + c3 x3 + 1			x5 x − 2	x3 x2 + x x3 .
	5		3

Пример 2. Найти решение уравнения y′′+4y =	1		.
	2	x
	sin

Решение. Характеристическое уравнение r2 + 4 = 0 имеет корни r1,2 = ± 2i, а потому общее решение однородного уравнения

u = c1cos2x + c2sin2x.

Частное решение исходного уравнения методом неопределённых коэффициентов искать нельзя, а потому воспользуемся методом вариации произвольных постоянных. Будем искать частное решение в виде

y = c1(x)cos2x + c2(x)sin2x,

при этом производные функций c1(x) и c2(x) можно найти из сис-

темы уравнений

′

(x)cos2x +

′

(x)sin 2x = 0,

с1

с2

−2c1′(x)sin 2x +2c2′(x)cos 2x =

1

.

2

x

sin

Решая эту систему, получаем

1

1

с1′(x) = −ctqx,

′

1

(ctq

2

x −1)=

−2

, откуда

2

c2 (x) = −

2

2

x

sin

c1 (x) = −∫ctqxdx = −ln

sin x

+c3 ,

1

1

1

c

(x) =

−2

dx

= −

ctqx − x +c

4 .

2

x

2

2

∫ sin 2

Таким образом, частное решение								исходного уравнения можно
					1
взять в виде	y = −ln	sin x		cos 2x −		ctqx + x sin 2x ,				при этом общее ре-
					2
шение									1
y = u + y = c1cos2x + c2sin2x −ln							sin x	cos 2x −	2	ctqx + x sin 2x .