
Konspekt_lekcij / Lekciya_9
.docЛекция № 9.
Z-преобразование.
Удобным способом анализа дискретных последовательностей является Z-преобразование. При Z-преобразовании разностные уравнения, описывающие работу дискретной системы, преобразуются в алгебраические уравнения, с которыми проще производить необходимые действия. Z-преобразование играет для дискретных сигналов и систем такую же роль, как преобразование Лапласа – для аналоговых сигналов.
Определение Z-преобразования.
Дискретной последовательности
отсчетов
![]() ставится в соответствие функция
комплексной переменной z,
определяемая следующим образом:
ставится в соответствие функция
комплексной переменной z,
определяемая следующим образом:
![]() (9.1)
(9.1)
Функция
![]() определена только для тех значений z,
при которых ряд (9.1) сходится.
определена только для тех значений z,
при которых ряд (9.1) сходится.
Если последовательность
![]() имеет
ограниченную длину, то
имеет
ограниченную длину, то
![]() сходится в Z-плоскости
везде, за исключением, быть может, точек
z = 0 или z =
сходится в Z-плоскости
везде, за исключением, быть может, точек
z = 0 или z =
![]() .
.
Получим Z-преобразование для некоторых часто встречающихся на практике дискретных сигналов.
Единичный импульс, определяемый как
![]() .
(9.2)
.
(9.2)
Используя формулу (9.1), получаем:
![]() (9.3)
(9.3)
Функция
![]() сходится во всей комплексной плоскости.
сходится во всей комплексной плоскости.
Единичный скачок, определяемый соотношением:
![]() .
(9.4)
.
(9.4)
Используя определение Z-преобразования, получаем:
![]() (9.5)
(9.5)
Ряд (9.5) является суммой бесконечной
геометрической прогрессии с первым
членом 1 и знаменателем
![]() .
Как известно, такой ряд сходится при
.
Как известно, такой ряд сходится при
![]() то есть при
то есть при
![]() и его сумма равна:
и его сумма равна:
![]() (9.6)
(9.6)
Значение
![]() является единственной особой точкой
(полюсом) функции
является единственной особой точкой
(полюсом) функции
![]() .
.
Экспоненциальная дискретная функция, определяемая как
 .
(9.7)
.
(9.7)
![]() (9.8)
(9.8)
Как и в предыдущем случае, этот ряд
представляет собой сумму геометрической
прогрессии с первым членом, равным 1 и
знаменателем
![]() .
Таким образом, ряд сходится при
.
Таким образом, ряд сходится при
![]() т.е. при
т.е. при
![]() ,
и имеет особую точку при
,
и имеет особую точку при
![]() :
:
![]() (9.10)
(9.10)
Комплексная дискретная экспонента, определяемая как
 .
(9.11)
.
(9.11)
![]() (9.12)
(9.12)
причем
![]() сходится при
сходится при
![]() ,
т.к. единственной особой точкой
,
т.к. единственной особой точкой
![]() является
является
![]() .
.
Связь Z-преобразования с преобразованием Лапласа найдем, записав аналоговый сигнал в виде суммы дискретных отсчетов и набора дельта-функций:
![]() (9.13)
(9.13)
где
![]() шаг
дискретизации. Преобразование Лапласа
для такого сигнала равно:
шаг
дискретизации. Преобразование Лапласа
для такого сигнала равно:
![]() (9.14)
(9.14)
Воспользовавшись фильтрующим свойством дельта-функции, получим:
![]() (9.15)
(9.15)
Сравнивая соотношения (9.1) и (9.15), замечаем,
что одна формула переходит в другую при
замене
![]() .
Таким образом, Z-преобразование
можно получить из преобразования Лапласа
путем перехода к новой переменной:
.
Таким образом, Z-преобразование
можно получить из преобразования Лапласа
путем перехода к новой переменной:
![]() (9.16)
(9.16)
Смысл использования Z-преобразования при анализе дискретных сигналов вытекает из следующего. Так как справедливо соотношение:
![]() ,
(9.17)
,
(9.17)
то изменение фазовой характеристики
сигнала
![]() означает задержку сигнала на один шаг
дискретизации
означает задержку сигнала на один шаг
дискретизации
![]() и соответствует задержке сигнала на
один такт в
и соответствует задержке сигнала на
один такт в
![]() области.
области.
Переход от преобразования Лапласа к
Z-преобразованию при
описании дискретных систем необходим
по следующей причине. Дискретизация
аналогового сигнала приводит к
периодичности частотного спектра, то
есть появлению бесконечного ряда
сдвинутых копий спектра исходного
непрерывного сигнала. Очевидно, эффект
дискретизации приводит к появлению в
плоскости
![]() бесконечной конфигурации особых точек
(полюсов и нулей), повторяющихся через
интервал
бесконечной конфигурации особых точек
(полюсов и нулей), повторяющихся через
интервал
![]() .
.
При переходе от
![]() плоскости
к
плоскости
к
![]() плоскости
точка
плоскости
точка
![]() отображается в точку
отображается в точку
![]() .
Поэтому путь вдоль мнимой оси
.
Поэтому путь вдоль мнимой оси
![]() в
в
![]() плоскости
отображается в единичную окружность
в
плоскости
отображается в единичную окружность
в
![]() плоскости,
так как на мнимой оси
плоскости,
так как на мнимой оси
![]() и, следовательно
и, следовательно
![]() Можно показать, что левая (устойчивая)
полоса
Можно показать, что левая (устойчивая)
полоса
![]() плоскости
шириной
плоскости
шириной
![]() отображается внутрь круга единичного
радиуса
отображается внутрь круга единичного
радиуса
![]() плоскости.
Все последующие полосы
плоскости.
Все последующие полосы
![]() плоскости
шириной
плоскости
шириной
![]() ,
соответствующие периодическому
частотному спектру дискретного сигнала,
также отображаются внутрь круга
единичного радиуса
,
соответствующие периодическому
частотному спектру дискретного сигнала,
также отображаются внутрь круга
единичного радиуса
![]() плоскости.
Поэтому конфигурация особых точек
(полюсов и нулей) в
плоскости.
Поэтому конфигурация особых точек
(полюсов и нулей) в
![]() плоскости
становится конечной.
плоскости
становится конечной.
Свойства Z-преобразования.
-
Линейность.
Если
![]() и
и
![]() являются Z-преобразованиями
соответствующих сигналов
являются Z-преобразованиями
соответствующих сигналов
![]() и
и
![]() ,
то сигналу
,
то сигналу
![]() будет
отвечать Z-преобразование
будет
отвечать Z-преобразование
![]() при любых постоянных
при любых постоянных
![]() и
и
![]()
-
Задержка (сдвиг последовательности).
Если Z-преобразование
сигнала
![]() равно
равно
![]() ,
то Z-преобразование сигнала
,
то Z-преобразование сигнала
![]() ,
задержанного на
,
задержанного на
![]() тактов, будет равно
тактов, будет равно
![]() .
.
Доказательство.
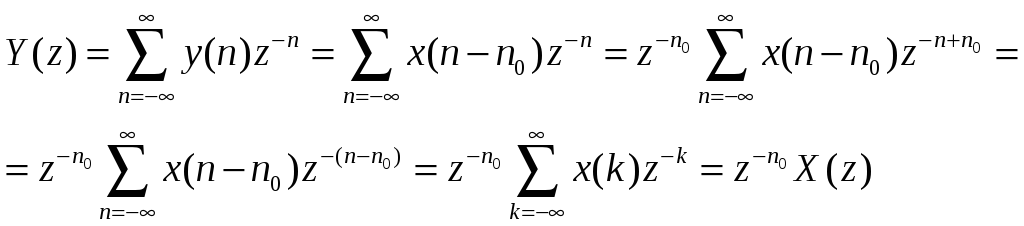 (9.18)
(9.18)
Таким образом, при задержке сигнала на
![]() тактов необходимо умножить его
Z-преобразование на
множитель
тактов необходимо умножить его
Z-преобразование на
множитель
![]() .
.
В частности, если сигнал
![]() получен путем сдвига сигнала
получен путем сдвига сигнала
![]() на один такт в сторону запаздывания, то
его Z-преобразование
на один такт в сторону запаздывания, то
его Z-преобразование
![]() .
Следовательно, символ
.
Следовательно, символ
![]() служит оператором единичной задержки
(на один интервал дискретизации) в
служит оператором единичной задержки
(на один интервал дискретизации) в
![]() области.
области.
3. Свертка.
Введем дискретную линейную свертку
![]() ,
которую определим следующим образом:
,
которую определим следующим образом:
![]() (9.19)
(9.19)
Вычислим ее Z-преобразование:
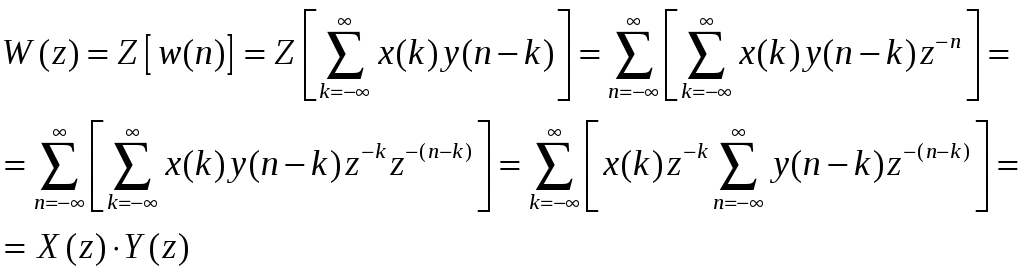 (9.20)
(9.20)
Итак, Z-преобразование линейной свертки двух дискретных сигналов равно произведению их Z-преобразований.
Системная функция (передаточная функция) дискретного фильтра.
Применим третье свойство Z-преобразования
к уравнению дискретной фильтрации:
![]() .
Поскольку выходной сигнал дискретной
системы есть линейная свертка входного
сигнала с импульсной характеристикой
системы, то
.
Поскольку выходной сигнал дискретной
системы есть линейная свертка входного
сигнала с импульсной характеристикой
системы, то
![]() ,
(9.21)
,
(9.21)
где
![]() –
Z-преобразования
соответственно входного и выходного
сигналов системы, а
–
Z-преобразования
соответственно входного и выходного
сигналов системы, а
![]() –
Z-преобразование ее
импульсной характеристики:
–
Z-преобразование ее
импульсной характеристики:
![]() .
(9.22)
.
(9.22)
Учитывая, что
![]() равняется отношению двух
равняется отношению двух
![]() преобразованных
сигналов (выходного и входного), ее
называют системной или передаточной
функцией. Она играет важнейшую роль
в построении дискретных цифровых систем.
преобразованных
сигналов (выходного и входного), ее
называют системной или передаточной
функцией. Она играет важнейшую роль
в построении дискретных цифровых систем.
Применим Z-преобразование к обеим частям разностного уравнения:
![]() (9.23)
(9.23)
Отсюда получаем общий вид передаточной функции:
![]() (9.24)
(9.24)
Таким образом, передаточная (системная)
функция физически реализуемой дискретной
системы может быть представлена в виде
отношения полиномов по отрицательным
степеням переменной
![]() .
.
