Дискретная математика / ДМ_Комбинаторика

Пример решения задания 5.2.

Игральная кость бросается 4 раза. Во сколько раз число способов набора суммы в 13 очков превышает число способов набора суммы в 17 очков?

Решение. Перейдём от кости, грани которой помечены символами 1, 2, …, 6, к кости, грани которой помечены цифрами 0,1, …, 5. Тогда суммам в 13 и 17 очков, полученным с помощью обычной кости, будут соответствовать суммы в 13 – 4 = 9 и 17 – 4 = 13 очков, полученные с помощью кости с нестандартной разметкой. Результаты бросаний нестандартной кости, выписанные подряд, можно интерпретировать как четырёхзначное число в шестеричной системе счисления.

Количества четырёхзначных чисел в шестеричной системе счисления, с суммами цифр 9 и 13, равны соответственно C6 4, 9 и C6 4, 13 . Заметим, что C6 4, 13 C6 4, 5 4 13 C6 4, 7 .

Для нахождения этих чисел построим обобщённый арифметический треугольник шестого порядка.

	k	0	1	2	3	4	5	6	7	8	9
n
1		1	1	1	1	1	1	0	0	0	0
2		1	2	3	4	5	6	5	4	3	2
3		1	3	6	10	15	21	25	27	27	25
4									104		140

Из таблицы видим, что C6 4, 7 104 , C6 4, 9 140 . Тогда

C		4,	9		140
6							1,346 .
C		4,	7		104
	6

Ответ: в 1,346 раза.

Задание 5.3. Запускается n волчков, у каждого из которых по m граней с нанесёнными на них числами p, p + 1, …, p + m – 1. Сколькими способами эти волчки могут упасть, набрав сумму в k очков, если волчки: 1) различимы? 2) неразличимы?

21

Если число способов не превосходит 10, то выписать эти способы.

Пример решения задания 5.3.

Запускается 4 волчка, у каждого из которых по 4 грани с нанесёнными на них числами 5, 6, 7, 8. Сколькими способами эти волчки могут упасть, набрав сумму в 25 очков, если волчки: 1) различимы? 2) неразличимы?

Решение. Перейдём от данных волчков к волчкам, грани которых помечены цифрами 0, 1, 2, 3. Тогда сумме 25, полученной с помощью исходных волчков, будет соответствовать сумма 25 – 5 · 4 = 5 для волчков с обновлённой нумерацией. В дальнейшем будем пользоваться только волчками с обновлённой нумерацией. Рассмотрим случаи:

1) волчки различимы. Тогда каждому способу набора волчками суммы в 5 очков соответствует четырёхзначное число в четверичной системе счисления, сумма цифр которого равна 5, а количество таких чисел равно C4 4, 5 . Для нахождения количества таких чисел построим обобщённый арифметический треугольник четвёртого порядка.

	k	0	1	2	3	4	5
n
1		1	1	1	1	0	0
2		1	2	3	4	3	2
3		1	3	6	10	12	12
4							40

Из таблицы видим, что C4 4, 5 40 .

2) волчки неразличимы. В этом случае введём функцию fm n, k – количество способов набора суммы k на n волчках, если m – максимальная выпавшая величина баллов.

Справедлива рекуррентная формула

	fm n, k fm 1 n, k fm 1 n 1, k m fm 1 n 2, k 2m fm 1 n t, k tm ,
где t		k	. Для нашего случая будем иметь:
	m
		22

f3 4, 5 f2 4, 5 f2 3, 2 ;

f2 4, 5 f1 4, 5 f1 3, 3 f1 2, 1 0 1 1 2 ; f2 3, 2 f1 3, 2 f1 2, 0 1 1 2 .

В итоге получим: f3 4, 5 f2 4, 5 f2 3, 2 2 2 4 .

Выпишем 4 возможные комбинации:

0 + 0 +2 + 3, 0 + 1 + 1 + 3, 0 + 1 + 2 + 2, 1 + 1 + 1 + 2.

Ответ: 1) 40 способов; 2) 4 способа.

Задание 5.4. Сколькими способами можно оплатить марками бандероль на сумму k рублей, если есть неограниченное число марок достоинством в a, b, c рублей и два способа, отличающиеся только порядком наклейки марок, считаются: 1) различными? 2) одинаковыми?

Если число способов не превосходит 10, то выписать их.

Пример решения задания 5.4.

Решим задания для k = 20, a = 6, b = 5, c = 3.

1) Пусть f k означает число способов, которыми можно оплатить сумму в k рублей мар-

ками достоинством в 6, 5 и 3 рубля, при условии неограниченности числа марок каждого из достоинств и два способа, отличающиеся лишь порядком наклейки марок, считаются различными. Тогда справедлива рекуррентная формула

f k f k 6 f k 5 f k 3 .

Эта формула позволяет вычислять значения функции в точке k через значения функции в точках k 6 , k 5 , k 3 .

Очевидно, что при k 0	f k 0 . Далее,	f 0 1,	f 1 0 ,	f 2 0 ,	f 3 1,	f 4 0 ,
	f 5 1,	f 6 2 ;

f 7 f 1 f 2 f 4 0 0 0 0 ; f 8 f 2 f 3 f 5 0 1 1 2 ; f 9 f 3 f 4 f 6 1 0 2 3 ;

f 10 f 4 f 5 f 7 0 1 0 1; 23

f 11 f 5 f 6 f 8 1 2 2 5 ; f 12 f 6 f 7 f 9 2 0 3 5 ; f 13 f 7 f 8 f 10 0 2 1 3; f 14 f 8 f 9 f 11 2 3 5 10 ;

f 15 f 9 f 10 f 12 3 1 5 9 ; и т.д.

f 17 f 11 f 12 f 14 5 5 10 20 ; и т.д. f 20 f 14 f 15 f 17 10 9 20 39 .

Итак, f 20 39 .

2) Пусть g k; n1, n2 , , n p означает число способов, которыми можно оплатить сумму в k рублей марками достоинством n1, n2, , np рублей, если число марок каждого достоинства не-

ограниченно и два способа, отличающиеся только порядком наклейки марок, считаются одинаковыми.

В нашем случае справедлива рекуррентная формула:

g 20; 6, 5, 3 g 20; 5, 3 g 14; 5, 3 g 8; 5, 3 g 2; 5, 3 .

Первое слагаемое в правой части равенства соответствует случаю, когда 6-рублёвые марки не участвуют в оплате суммы, второе – когда ровно одна 6-рублёвая марка участвует в оплате суммы и т.д.

Очевидно, что g 2; 5, 3 0 , а для каждого из остальных слагаемых составим, руководствуясь тем же принципом, рекуррентные формулы:

g 20; 5, 3 g 20; 3 g 15; 3 g 10; 3 g 5; 3 g 0; 3 ; g 14; 5, 3 g 14; 3 g 9; 3 g 4; 3 ;

g 8; 5, 3 g 8; 3 g 3; 3 .

Ясно, что

1, если k кратно n, g k; n

0, если k не кратно n.

Поэтому имеем:

g 20; 5, 3 0 1 0 0 1 2 ; g 14; 5, 3 0 1 1; g 8; 5, 3 0 1 1; g 20; 6, 5, 3 2 1 1 0 4 .

Выпишем соответствующие представления:

20 5 5 5 5; 20 5 3 3 3 3 3; 20 6 5 3 3 3; 20 6 6 5 3.

Ответ: 1) 39 способов; 2) 4 способа.

24

6. Рекуррентные соотношения

Рекуррентным соотношением k-го порядка называется формула, позволяющая выражать значения члена последовательности с номером n (n > k) через члены этой последовательности с номерами n – 1, n – 2, …, n – k.

Решением рекуррентного соотношения называется числовая последовательность xn f n , обращающая его в верное равенство по n при подстановке в соотношение формулы общего члена последовательности.

Начальными условиями рекуррентного соотношения k-го порядка называются первые k

членов последовательности, являющиеся решением данного рекуррентного соотношения.

Линейным однородным рекуррентным соотношением k-го порядка с постоянными коэф-

фициентами называется соотношение вида

f n k a1 f n k 1 a2 f n k 2 ak f n .

( )

Общим решением соотношения ( ) называется такое его решение, которое содержит k произвольных постоянных, путём подбора которых можно удовлетворить любым начальным условиям и получить частное решение соотношения ( ).

Характеристическим уравнением соотношения ( ) называется уравнение:

xk a xk 1	a	2	xk 2 a	k	.	( )
1

Теорема. Общее решение соотношения ( ) имеет вид: f n A1 A2 Ap ,

где

Ai Ci xn , Ci – произвольная постоянная,

если х – действительный корень первой кратности характеристического уравнения ( );

Ai Ci,1 nCi,2 n2Ci,3 nm 1Ci,m xn , Ci,1, Ci,2 , ,Ci,m – произвольные постоянные,

если х – действительный корень кратности m уравнения ( );

Ai r n Di cos n Ei sin n , Di , Ei – произвольные постоянные,

если r cos i sin – комплексно-сопряжённая пара корней первой кратности уравнения ( );

Ai r n Di,1 nDi,2 n2 Di,3 nm 1Di,m cos n Ei,1 nEi,2 n2 Ei,3 nm 1Ei,m sin n ,

Di,1, Di,2 , Di,m , Ei,1, Ei,2 , Ei,m – произвольные постоянные,

если r cos i sin – комплексно-сопряжённая пара корней кратности m уравнения ( ).

Задание 6.1. Найти общее решение линейного однородного рекуррентного соотношения 5- го порядка

f n 5 a f n 4 b f n 3 c f n 2 d f n 1 e f n .

25

Пример решения задания 6.1.

Найти общее решение рекуррентного соотношения 5-го порядка

f n 5 4 f n 4 4 f n 3 2 f n 2 5 f n 1 2 f n .

Решение. Запишем характеристическое уравнение данного соотношения:

x5 4 x4 4 x3 2 x2 5 x 2 0 .

Непосредственной подстановкой в уравнение убеждаемся, что x1 1 является корнем характеристического уравнения.

Понизим степень уравнения, поделив характеристический многочлен на x 1 по схеме Горнера:

	1	– 4	4	2	– 5	2
1	1	– 3	1	3	– 2	0

В результате деления приходим к уравнению четвёртой степени:

x4 3 x3 x2 3 x 2 0 .

Заметим, что x2 1 является корнем и этого уравнения, разделим левую часть уравнения

на тот же двучлен x 1:
		1		– 3	1	3	– 2
	1	1		– 2	– 1	2	0
Получим уравнение x3 2 x2			x 2 0 , которое также имеет x						1 своим корнем. По-

3

нижаем степень этого уравнения:

26

								1			– 2		– 1		2
					1			1			– 1		– 2		0
В результате приходим к уравнению x2 x 2 0 , которое имеет два действительных кор-
ня x4 1 и x5	2 . Таким образом, характеристическое уравнение имеет корень x1 кратности 3
и два корня x4 ,	x5 первой кратности.
По теореме о виде общего решения линейного однородного рекуррентного соотношения с
постоянными коэффициентами, запишем общее решение:
f n C nC		2	n2C	1n C		4		1 n C 2n				C nC			2	n2C C		4	1 n C 2n .
1			3							5			1				3		5
Ответ: f	n C nC			2	n2C			C	4	1 n C			2n .
			1		3					5

Задание 6.2. Найти общее решение рекуррентного соотношения 5-го порядка

f n 5 a f n 4 b f n 3 c f n 2 d f n 1 e f n .

Пример решения задания 6.2.

Найти общее решение рекуррентного соотношения 5-го порядка

f n 5 23 f n 4 4 f n 3 2 f n 2 43 f n 1 8 f n .

Решение. Запишем характеристическое уравнение данного соотношения:

x5 23 x4 4 x3 2 x2 43 x 8 0 .

Спомощью группировки разложим левую часть на множители:

x3 x2 23 x 4 2 x2 23 x 4 0 ,

27

или										x3 2 x2											2					x 4 0 .
																									3
Рассмотрим два случая:
																			i arg 2 2 k															i 2 k
1) x3 2 0 ,	x3 2																												3
				, x		k		3				2						e					3							2 e						3			, k 0,1, 2 . Получим
										3							e 3 i				3				cos i sin ,
							x		0						2									2
																											3
																																	3
								3						ei 3									cos i sin 3
					x						2										2														2,
						1
					5			i												5							5
	x2 3 2 e 3										3 2 cos												i sin							3 2 cos								i sin			.
																				3							3									3				3

Тогда соответствующие слагаемые в общем решении будут иметь вид:

			C			n		3		n			n				n
				3 2					2			cos		C		sin
										C							.
			1								2		3		3		3
2) x2 2
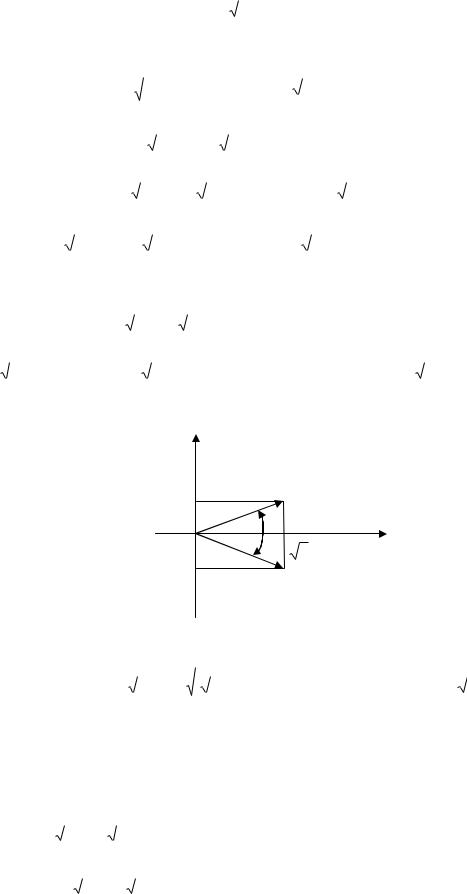
	3 x 4 0		, x				3 i . Изобразим комплексные числа											3 i на комплексной
			3,4

плоскости для нахождения их модулей и аргументов (рис.1).

1
0	3
‒ 1

				Рис. 1
							2 12
Получим, что модуль r		3 i				3		2 , аргументы	arctg	3			. Соот-
												6

ветствующие слагаемые в общем решении будут иметь вид:

								2		n						n	C5 sin						n
											C4 cos					6							.
																							6
Таким образом, общее решение исходного рекуррентного соотношения
f n C 3		n					n					cos			n	C			sin			n				cos			n	C			sin			n
	2			3 2				C															2n C														.
1											2				3			3				3			4				6			5				6
Ответ: f n C 3				n	3				n					cos		n	C				sin		n	2n				cos		n	C				sin		n
			2					2			C														C												.
1													2			3				3			3				4			6				5			6

Задание 6.3. Найти общий вид решения рекуррентного соотношения 4-го порядка xn 4 a xn 3 b xn 2 c xn 1 d xn 0 , если x0 0 .

28

Пример решения задания 6.3.

Найти общий вид решения рекуррентного соотношения 4-го порядка xn 4 3 xn 3 8 xn 1 24 xn 0 , если x0 0 .

Решение. Запишем характеристическое уравнение данного соотношения:

x4 3 x3 8 x 24 0 .

Непосредственной подстановкой убеждаемся, что среди делителей свободного члена характеристического уравнения x1 2 – корень уравнения. Понизим степень уравнения, поделив характеристический многочлен на x 2 по схеме Горнера:

29

	1	– 3	0	– 8	24
2	1	– 1	– 2	– 12	0

В результате деления исходное уравнение сводится к уравнению третьей степени:

x3 x2 2 x 12 0 .

Аналогично, непосредственной проверкой убеждаемся, что x2 3 является корнем этого уравнения. Разделим левую часть уравнения на x 3 :

															1					– 1				– 2					– 12
								3							1					2				4							0
								x2 2x2							4 0 , которое имеет корни																			x 1 i
Приходим к уравнению																																				3 . Комплекс-
																																		3,4
ные числа 1 i															и аргументы											2			.
		3 имеют модуль r 2
																											3
Учитывая все корни характеристического уравнения, запишем общее решение рекуррент-
ного соотношения:
						C 2			n	C						n	2		n					2n		C						2n
				x											3					C		cos									sin			.
					n			1					2								3			3						4		3
Так как x	0		0 , то 0 C 20							C		2		30			20 C cos 0 C									4	sin 0 ,					откуда C C			2	C . Подста-
								1												3														1		3

вим полученное выражение в формулу общего решения и получим общий вид решения, удовлетворяющего начальному условию:

xn C2 C3 2

n

C2

n

2

n

2n

C4 sin

2n

3

C3 cos

.

3

3

Ответ: xn C2 C3 2

n

C2

n

2

n

2n

C4 sin

2n

3

C3 cos

.

3

3

Задание 6.4. Найти частное решение рекуррентного соотношения 4-го порядка f n 4 f n 3 f n 2 f n 1 f n ,

удовлетворяющее начальным условиям для f 0 , f 1 , f 2 , f 3 .

30