Дискретная математика / ДМ_Комбинаторика

ЧАСТЬ II. КОМБИНАТОРИКА И РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ

1.Сочетания, размещения, перестановки

Косновным правилам комбинаторики относят: правило умножения (произведения) и правило сложения (суммы).

Правило умножения:

если элемент (объект, предмет) a1 можно выбрать n1 способами; после каждого выбора этого элемента следующий за ним элемент a2 можно выбрать n2 способами; после каждого выбора элементов a1, a2 элемент a3 можно выбрать n3 способами, и т.д., после каждого выбора элементов a1, a2,…, ak–1 элемент ak выбирается nk способами, то все k элементов a1, a2, …, ak можно выбрать n1 n2 nk способами.

Правило сложения:

если элемент (объект, предмет) a1 можно выбрать n1 способами; элемент a2 можно выбрать n2 способами так, что ни один из способов выбора элемента a2 не совпадает со способами выбора элемента a1; элемент a3 можно выбрать n3 способами, не совпадающими со способами выбора элементов a1 и a2, и т.д., наконец, элемент ak можно выбрать nk способами, не совпадающими со способами выбора элементов a1, a2,…, ak–1, то выбрать элемент a1 или a2 или …или ak («или» здесь логическое) можно n1 n2 nk способами.

Пусть имеется n предметов, отмеченных числами 1, 2, …, n. Из этих предметов выбираем один, записываем число, на нём изображённое, а сам предмет либо возвращаем назад (в этом случае говорят о выборе с возвращением), либо он удаляется и больше не может быть выбран (выбор без возвращения). Повторяем процедуру выбора k раз.

Запись, полученная в результате всех действий, называется выборкой из n по k. Говорят также, что получена выборка объема k из множества, содержащего n элементов. При этом запись, полученная по схеме выбора с возвращением, называется выборкой с повторениями, а запись, полученная по схеме выбора без возвращения, называется выборкой без повторений.

Если любые две выборки одного и того же объема, отличающиеся только порядком записи символов, считаются различными, то говорят о размещении из n элементов по k. Если же такие выборки считаются совпадающими, то говорят о сочетании из n элементов по k.

Число размещений с повторениями из n элементов по k обозначается Ank (Arrangement – расположение) и вычисляется по формуле

Ank nk .

Число размещений без повторений из n элементов по k обозначается Ank и вычисляется по формуле

Ak		n!		.
n		(n k)!

Число сочетаний без повторений из n элементов по k обозначается Cnk (Combination – сочетание, комбинация) и вычисляется по формуле

C k		Ak		n!
		n				.
n		k!		k!(n k)!

1

Число сочетаний с повторениями из n элементов по k обозначается Cnk и вычисляется по формуле

Cnk Cnk k 1 .

Размещение из n элементов по n называется перестановкой из n элементов. Любые две перестановки из n элементов имеют одинаковый состав и отличаются только порядком следования элементов. Число различных перестановок n элементов обозначается Pn (Permutation – переста-

новка) и вычисляется по формуле

Pn n!.

Пусть имеется k1 элементов 1-го типа, k2 элементов 2-го типа, и т.д., km элементов m-го типа, причём элементы одного типа считаются неразличимыми и объем выборки равен k1 k2 ... km . Перестановки такой выборки называют перестановками с повторениями. Число перестановок с повторениями обозначается P k1, k2 ,..., km и вычисляется по формуле

P k1, k2 ,..., km k1 k2 ... km ! . k1!k2!... km!

Задание 1.1. Сколькими способами из колоды карт в 36 листов можно выбрать неупорядоченный набор из 5 карт так, чтобы в этом наборе было бы точно:

2

Пример решения задания 1.1.

Сколькими способами из колоды карт в 36 листов можно выбрать неупорядоченный набор из 5 карт так, чтобы в этом наборе было бы точно два туза, одна дама, одна бубновая карта.

Решение. Так как бубновая карта может быть и тузом и дамой, а может и не быть ни тузом, ни дамой, то рассмотрим случаи:

1. Среди пяти выбранных карт есть бубновая дама.

Бубновую даму можно выбрать единственным способом, два туза будут выбираться из трёх небубновых тузов, так как бубновая карта уже выбрана, и сделать это можно C32 3 способами. К

выбранным трём картам надо добавить до пяти ещё две карты так, чтобы они не были дамами, тузами и бубновыми картами. Таких карт в колоде 36 4 4 7 21 штука. Число неупорядоченных

выборок из 21 по 2 карты без повторений равно C 2		21!			20 21	210 . По правилу произве-
21		2! 19!			2

дения, число способов выбора 5 карт, среди которых есть бубновая дама, равно 1 3 210 630 . 2. Среди пяти выбранных карт есть бубновый туз.

Бубнового туза можно выбрать единственным способом, второго туза к нему выбираем из оставшихся небубновых тузов C31 3 способами. Так как бубновая дама не может быть выбрана,

то выбрать одну даму из трёх небубновых можно C31 3 способами. К выбранным трём картам

остается добавить до пяти ещё две карты так, чтобы они не были тузами, дамами и бубновыми картами. Число способов выбора двух оставшихся карт, как и в предыдущем случае, равно 210. По

правилу произведения, число способов выбора 5 карт, среди которых есть бубновый туз, равно

1 3 3 210 1890 .

3. Среди пяти выбранных карт нет бубнового туза и бубновой дамы.

Одну небубновую даму можно выбрать C31 3 способами, два небубновых туза можно вы-

брать C32 3 способами, одну бубновую карту (бубновых карт 9), которая не является ни дамой,

ни тузом выбираем C91 2 C71 7 способами. Число способов выбора 5 карт, среди которых нет бубнового туза и бубновой дамы, по правилу произведения, равно 3 3 7 210 1323 .

Общее число способов выбора 5 карт, среди которых точно два туза, одна дама, одна бубновая карта, по правилу суммы, составит 630 1890 1323 3843.

Ответ: 3843 способа.

Задание 1.2. Сколько различных слов можно получить перестановкой букв слова так, чтобы ?

3

4

Пример решения задания 1.2.

Сколько различных слов (не обязательно осмысленных) можно получить перестановкой букв слова «огород» так, чтобы три буквы «о» не стояли бы рядом?

Решение. Общее количество различных слов, полученных перестановкой букв слова «огород», равно

P 3, 1, 1, 1 3 1 1 1 ! 6! 6 5 4 120 . 3! 1! 1! 1! 3!

Если в каком-то слове три буквы «о» стоят рядом, то эти три буквы будем считать единым символом. Тогда все такие слова будут состоять из 4 различных букв и число таких слов, в которых три буквы «о» стоят рядом, равно P4 4! 24 .

Количество различных слов, в которых три буквы «о» не стоят рядом, равно 120 24 96 .

Ответ: 96 слов.

2. Бином Ньютона и полиномиальная формула

Справедлива формула бинома Ньютона:

										n
								a x n Cnk a n k xk ,
										k 0
	где числа C k				n!		называют биномиальными коэффициентами.
		n		k!(n k)!
	Справедлива также полиномиальная формула:
										n
					x1 x2 xm n					P k1, k2 ,..., km x1k1 x2k2 xmkm ,
								k1	N 0	, , km N 0
								k1	k2	... km n
	где N0	0, 1, 2, – множество целых неотрицательных чисел, а числа
	P k1, k2	,..., km			k1 k2		... km !	называют полиномиальными коэффициентами.
					k1!k2		!... km!

Некоторые свойства биномиальных коэффициентов:

1)Cn0 Cnn 1 ; C1n Cnn 1 n ;

2)Cnk Cnn k (свойство симметричности);

3)	C k	C k 1 C k		1	(свойство арифметического треугольника);
	n	n 1	n
4)	Cn0 C1n Cn2		Cnn 2n ; Cn0 C1n Cn2 1 n Cnn 0 (свойства сумм)
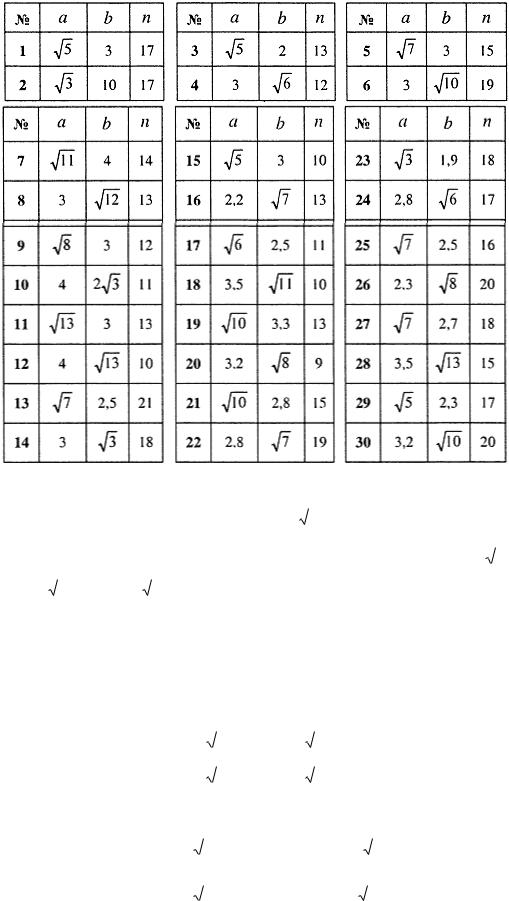
		Задание 2.1. Найти наибольший член разложения бинома a b n .

5

Пример решения задания 2.1.

Найти наибольший член разложения бинома 1

100 .

3

Решение. Пусть Tk

–

наибольший

член

разложения

бинома 1

100 . Имеем

3

C k

1100 k

k C k

k . В силу максимальности,

T

удовлетворяет системе нера-

T

3

3

k

100

100

k

венств

Tk

Tk 1,

Tk 1.

Tk

Подставив вместо Tk его выражение, приходим

C k

k

C k 1

k 1,

3

3

100

100

k

C k 1

k 1,

C k

3

3

100

100

или

3

3

,

100!

k

100!

k 1

(k 1)!(101 k)!

k!(100 k)!

100!

k

100!

k 1.

3

3

(k 1)!(99 k)!

k!(100 k)!

После сокращений имеем:

6

		3									1							,
		k
								101 k
		1															3
																						,
														k 1
100						k
или
(101 k)
											3 k,
k 1 (100 k) 3,
откуда
							101					3
k															,
							1
												3
																1
							100						3
k																				.
									1			3
Подставляя приближенное значение				3 1,732 , получим двойное неравенство для k:

63,135 k 64,64 .

Единственное целое значение k, удовлетворяющее этому двойному неравенству, равно 64. Следовательно, наибольший член разложения бинома имеет номер k 64 и

T64 C10064 3 64 64! 36!100! 332 .

Ответ: 64! 36!100! 332 .

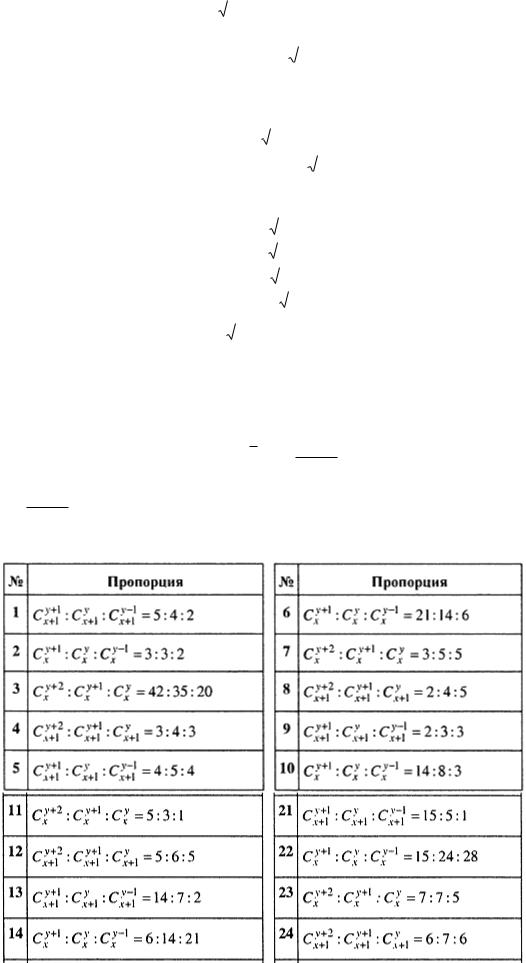
Задание 2.2. Из данной пропорции найти x и y.

7

Пример решения задания 2.2.

Из пропорции Cxy 1 : Cxy : Cxy 1 2 : 2 :1 найти x и y.

Решение. Записав отдельно отношение первого члена пропорции ко второму и второго к третьему, после сокращений получим:

x!

:

x!

x y

;

( y 1)!(x y 1)!

y!(x y)!

y 1

x!

:

x!

x y 1

.

y!(x y)!

( y 1)!(x y 1)!

y

По условию задачи приходим к системе уравнений:

x y			2			,
		2
y 1
		1					2
x y								.
	y						1

Решив эту систему, получим: x 5, y 2 .

Ответ: x 5, y 2 .

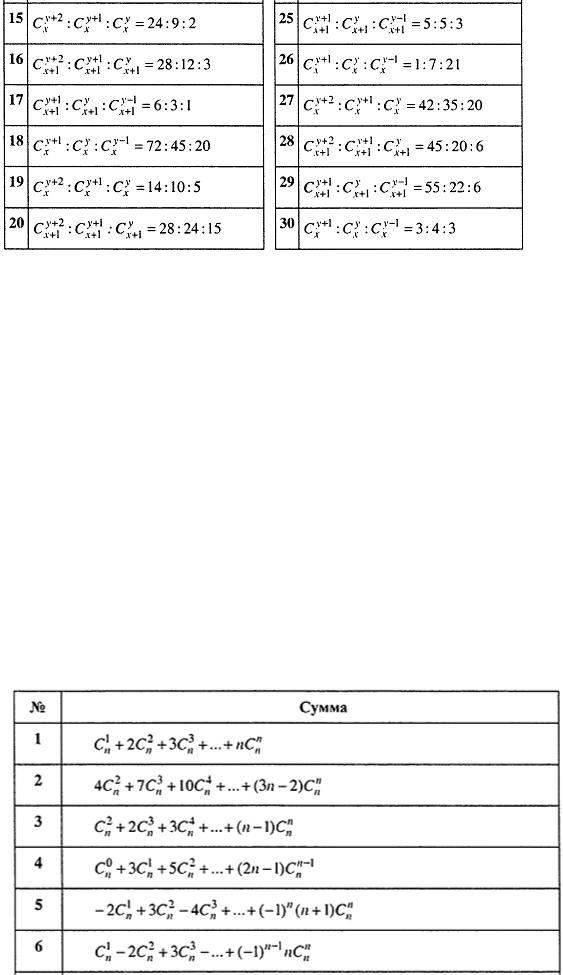
Задание 2.3. Вычислить данные суммы.

8

9

Примеры решения задания 2.3.

1)

Вычислить сумму C1

3C 2

5C3

2

2n 3 C n 2

n 1 .

n 2

n 2

n

n 2

Решение. Обозначим искомую сумму через S. Тогда

S 1 1 C 0

C1

3C 2

2

5C3

2

2n 1 C n 1 2n 3 C n 2

( )

n 2

n 2

n

n

n 2

n 2

Учитывая свойство симметричности, перепишем равенство ( ) в виде:

S 1 2n 3 C

0

2n 1 C1

2

2n 1 C 2

2n 3 C3

C n 1

C n 2

( )

n 2

n

n 2

n 2

n

2

n 2

Сложив равенства ( ) и ( ), получим:

2S 2 2n 2 C 0

2n 2 C1

2

2n 2 C 2

2n 2 C 3

n 2

n

n 2

n 2

2n 2 C n 1

2n 2 C n 2 ,

2n 2 C 0

n 2

n 2

C n 2 . Разделим обе части ра-

откуда 2 S 1

C1

C 2

C3

2

C n 1

n 2

n 2

n

2

n

n

2

n 2

венства

на

2

и

воспользуемся

свойством

биномиальных

коэффициентов

C 0

C1

C 2 C m

2m

. Приходим:

S 1 n 1 2m , откуда S n 1 2m 1.

m

m

m

m

Ответ: n 1 2m 1.

1

2

3

2

n

n 2

1 .

2)

Вычислить сумму Cn 2 3Cn 2

5Cn

1

2n 3 Cn 2 n

Решение. Обозначим искомую сумму через S. Тогда

S 1 Cn0 2 C1n 2 3Cn2 2 5Cn3 2 1 n Cnn 22 .

Можно считать, что S 1 f ' 1 ,

где

f ' x

Cn0 2

C1n 2

3Cn2 2 x2

5Cn3 2 x4 1 n 2n 3 Cnn 22 x2n 2 . Тогда одна из пер-

x2

f ' x будет иметь вид:

вообразных для

f x

Cn0 2

C1n 2 x Cn2 2 x3

Cn3 2 x5 1 n Cnn 22 x2n 3

x

или

f x

1

Cn0 2 C1n 2 x2 Cn2 2 x4

Cn3 2 x6 1 n 1Cnn 22 x2n 4 .

x

Свернув выражение в скобках по формуле бинома Ньютона, получим:

			f x	1 x2 n 2	.
				x
Тогда f ' x			1 x2 n 1 2nx2 3x2 1 . Если n 1, то			f ' x	x2 1 ,		f ' 1 2 . Если же
			x2				x2
n 1, то	f ' 1	1 12 n 1 2n 12 3 12 1 0 . Учитывая, что				S 1 f ' 1		или S f ' 1 1, по-

12

лучаем ответ.

10