Общие представления одношаговых методов решения обыкновенных дифференциальных уравнений

Пусть имеется дифференциальное уравнение

,

(1.25)

удовлетворяющее начальному условию

.

(1.26)

Требуется найти решение задачи (1.25), (1.26) на отрезке [x₀, x₀+X].Выполним разбиение отрезка точками

.

Этот набор точек называют сеткой, а точкиx_i(i = i,n) –узлами сетки.

Одношаговые численные методы дают приближения y_nк значениям точного решенияy(x_n) в каждом узле сеткиx_nна основе известного приближенияy_n-1к решению в предыдущем узлеx_n-1. В общем виде их можно представить так [6, 7]:

(1.27)

Для явных одношаговых методов функция Fне зависит отy_n+1.

Обозначая

явные одношаговые методы будем записывать также в виде

.

(1.28)

Явные методы типа Рунге-Кутта

Идея данного метода основана на вычислении приближённого решения y₁в узлеx₀ + hв виде линейной комбинации с постоянными коэффициентами [6, 7]:

(1.29)

где

Числа выбираются так, чтобы разложение выражения (1.29) по степенямhсовпадало с разложением в ряд Тейлора:

,

(1.30)

где ,,.

Это эквивалентно следующему. Если ввести вспомогательную функцию

,

(1.31)

то ее разложение по степеням hдолжно начинаться с максимально возможной степени:

.

(1.32)

Если можно определить эти постоянные так, чтобы разложение имело вид (1.32), то говорят, что формула (1.29) с выбранными коэффициентами имеет порядок точностиs.

Величина

(1.33)

называется погрешностью метода на шаге, илилокальной погрешностью метода, а первое слагаемое в выражении (1.32)

(1.34)

называется главным членом локальной погрешности метода.

Доказано, что если q = 1, 2, 3, 4, то всегда можно выбрать коэффициенты так, чтобы получить метод типа Рунге-Кутта порядка точностиq. Приq= 5 невозможно построить метод типа Рунге-Кутта (1.29) пятого порядка точности, необходимо брать в комбинации (1.29) более пяти членов.

Исследование кинетики гомогенных химических реакций

Исследование кинетических закономерностей протекания химической реакции методом математического моделирования заключается в определении изменения концентраций реагирующих веществ во времени при заданной температуре.

Пусть протекают химические реакции

.

На основании закона действующих масс запишем уравнения скоростей химических реакций и составим кинетическую модель:

; ; ; ; ; ,

(1.35)

где С_А, С_В, С_С,С_D– концентрации веществ, моль/л;

k_i – константа скорости i-й химической реакции первого порядка, с^-1; (для реакций второго порядка размерность константы; для реакций третьего порядка размерность константы);

W_i – скоростьi-й химической реакции, моль/лс;

t – время реакции, с.

Систему обыкновенных дифференциальных уравнений первого порядка (1.35) можно решить с использованием численного метода Эйлера, алгоритм которого записывается по уравнению (1.24).

Блок-схема расчета кинетики гомогенной химической реакции методом Эйлера приведена на рис. 1.2.

Рис. 1.2. Блок-схема расчета кинетики гомогенной химической реакции методом Эйлера

Примеры программ расчета кинетики гомогенных химических реакций приведены в Приложении А. Результаты исследования на математической модели (1.35) влияния температуры на степень превращения исходного реагента и на концентрацию веществ представлены на рис. 1.3, 1.4.

Полученные результаты позволяют сделать вывод об оптимальном времени проведения процесса с целью получения целевого продукта. Математическая модель (1.35) также позволяет исследовать влияние состава сырья на выход продуктов реакции.

Необходимо учитывать, что скорость химической реакции зависит от температуры, поэтому, чтобы использовать кинетическую модель (1.35) для исследования процесса при различных температурах, необходимо ввести зависимость константы скорости химической реакции от температуры по уравнению Аррениуса (1.9).

Алгоритм метода Рунге-Кутта четвертого порядка можно записать следующим образом:

, (1.36)

где a_i – коэффициенты Рунге-Кутта, которые рассчитываются по следующим формулам:

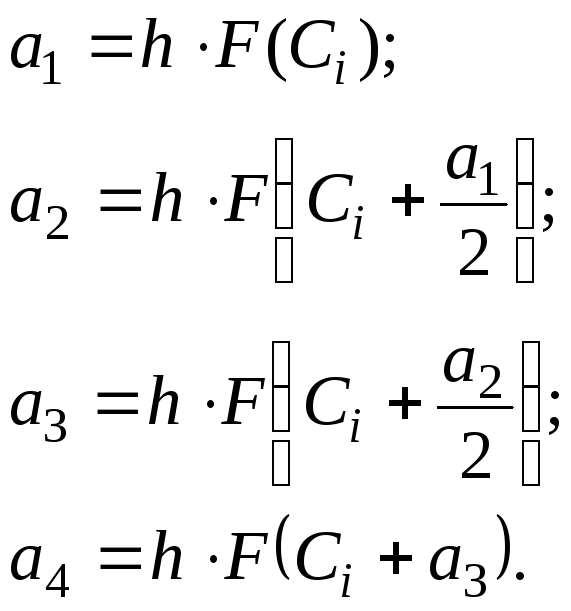; (1.37)