Kontrolnye_raboty_No3_i_No4

Учитывая, что заряд после присоединения второго конденсатора остался прежним, выразим разность потенциалов U2 следующим образом:

	U	2		Q			C1U1		.	(4)
				C C	2		C C	2
				1		1

Подставив выражение U2 в (3), найдем

W' C1U12 (C1 C2)C12U12 ,

2 2(C1 C2)2

	или	1			CC		U2 .
		W'			1	2
			2 C C
							1
				1		2

Произведем вычисления: W ' 1,5мДж.

Пример 12. Плоский воздушный конденсатор с площадью пластин S равной 500 см2, подключён к источнику тока, ЭДС которого равна ξ = 300В. Определить работу А внешних сил по раздвижению пластин от расстояния d1 = 1см до d2 =3 см в двух случаях: 1) пластины перед раздвижением отключались от источника тока; 2) пластины в процессе раздвижения остаются подключёнными к нему.

Решение

1-й случай. Систему двух заряженных и отключённых от источника тока пластин можно рассматривать как изолированную систему, по отношению к которой справедлив закон сохранения энергии. В этом случае работа внешних сил равна изменению энергии системы:

A W W2 W1 , (1)

где W1 – энергия поля конденсатора в начальном состоянии (пластины находились на расстоянии d1); W2 – энергия поля конденсатора в конечном состоянии (пластины находились на расстоянии d2).

Энергию в данном случае удобно выразить через заряд Q на пластинах, так как заряд пластин, отключённых от

21

источника, при раздвижении не изменяется. Подставив в равенство (1) выражения W2 Q2 /2C2 и W1 Q2 /2C1 , получим

	Q	2		Q	2			Q	2		1		1
А						, или	А							.
	2C2										C2
				2C1			2						C1

Выразив в этой формуле заряд через ЭДС источника тока и

начальную электроёмкость С1				(Q C1 ), найдём
2			2		1		1
А	C1							.	(2)
					C2		C1
2
Подставляя в формулу		(2)			выражения				электроёмкости

(C1 0S /d1 и C2		0S /d2 ) плоского конденсатора, получим
	2S2 2 d							2		d					0	S 2
А		0									1							d2 d1 .	(3)
		2d		2											2d		2
							0	S			0	S
			1													1

Произведя вычисления по формуле (3), найдём

А 8,85 10 12 500 10 4 3002 3 1 10 2 3,98мкДж. 2(1 10 2)2

2-й случай. Пластины остаются подключёнными к источнику тока и система двух пластин уже не является изолированной. Воспользоваться законом сохранения энергии в этом случае нельзя.

При раздвижении пластин конденсатора разность их потенциалов не изменяется (U=ξ), а ёмкость будет уменьшаться (C 0S/d). Будут уменьшаться также заряд на пластинах

конденсатора (Q=CU) и напряжённость электрического поля (Е=U/d). Так как величины E и Q , необходимые для вычисления работы, изменяются, то работу следует вычислять путём интегрирования.

dA QE1dx,

(4)

где Е1 – напряжённость поля, создаваемого зарядом одной пластины.

22

Выразим напряжённость поля E1 и заряд Q через расстояние x между пластинами:

		E		1	E							и		Q C ,												или		Q				S		.
	1		2						2x																						0	x
Подставив эти выражения E1																	и Q в равенство (4), получим
											dA					1					S		2			dx.
															2				0 x2
Проинтегрировав это равенство в пределах от d1																																						до d2,
найдём выражение для искомой работы:
	1		2 d2			dx 1											2			1						d2		1			2	1					1
A		0S										0S																	0S										.
							2
	2			d1		x			2													x				d1		2				d1					d	2
	После упрощения последняя формула имеет вид
												1					S 2(d						2		d )
									A						0											1	.
																					d d
												2														2
																				1
Сделав вычисления, получим																				A =1,33 мкДж.

Пример 13. Металлический шар радиусом R1=3см несёт заряд Q = 20 нКл. Шар окружён слоем парафина толщиной d = 2см. Определить энергию W электрического поля, заключённого в слое диэлектрика.

Решение

Поле, созданное заряженным шаром является неоднородным, поэтому энергия поля в слое диэлектрика распределена неравномерно. Однако объёмная плотность энергии будет одинакова во всех точках, отстоящих на равных расстояниях от центра сферы, т.к. поле заряженного шара обладает сферической симметрией.

Выразим энергию в элементарном сферическом слое диэлектрика объёмом dV:

dW dV ,

где ω – объёмная плотность энергии.

23

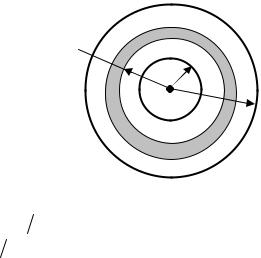
Полная энергия выразится интегралом

R d
W dV 4	r2dr,	(1)
R
где r – радиус элементарного сферического слоя; dr –		его

толщина.

dr

R

r

R+d

Объёмная плотность энергии определяется по формуле

0E2 2, где Е – напряжённость поля.							В нашем случае
E Q	4 0r2 и следовательно,
		Q2				.	(2)
		32	2	0r	4

Подставив это выражение в формулу (1) и вынеся за знак интеграла постоянные величины, получим

W	Q2	R d dr			Q2			1		1			Q2d	.
	8 0	R r2			8								8 0R(R d)
						0		R		R d

Произведя вычисления по этой формуле, найдём

W = 12 мкДж.

24

2.2.Постоянный электрический ток

2.2.1.Основные законы и формулы

1.Сила и плотность электрического тока

I dq ;j= dI en u , dt dS

где u , – средняя скорость упорядоченного движения

зарядов; n – концентрация зарядов. Сопротивление и проводимость проводника

R	dl	;		1	,
	S

где - удельное сопротивление.

2. Обобщенный закон Ома в дифференциальной и интегральной формах

			I (		)/ R,
j (E E);				2
			1

где E*- напряженность поля сторонних сил; 1 2 - разность потенциалов на концах участка цепи; ξ- ЭДС источников тока, входящих в участок

3. Закон Джоуля–Ленца в дифференциальной и интегральной формах

jE E2;

Q RI2dt,

где - удельная тепловая мощность тока. 4. Правила Кирхгофа

n	n	n
Ik 0;	Ik RK k .
k 1	k 1	k 1

25

2.2.2. Примеры решения задач

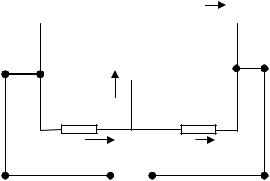
Пример 1. Найдите заряд на конденсаторе в схеме, изображенной на рисунке.

				c				I1
								3R
	C			I1
a							2R		d

R 4R

I0 b I2

U0

Решение

Постоянный ток через конденсатор не проходит и в ветви, где он включен, тока нет. Поэтому ток I0, идущий от источника напряжения UO, пойдет по резистору R и разветвится в точке b на токи I1 и I2, не заходя в ветвь ас. Заряд на конденсаторе

q = C·Uac ,	(1)
где
Uac = U1 + U2 .	(2)

Здесь U1 и U2 - падения напряжений на резисторах сопротивлением R и 2R соответственно:

U1 =I0· R , U2=I1·2R .

Для их нахождения воспользуемся правилами расчета последовательной и параллельной цепей, упростив схему.

Применим закон Ома ко всей цепи

I

U0

U0

9

U0

.

(3)

0

(2R 3R) 4R

R

общ

R

29 R

2R 3R 4R

26

2R

c

3R

b

a

I1

d

4R

I0

I2

U0

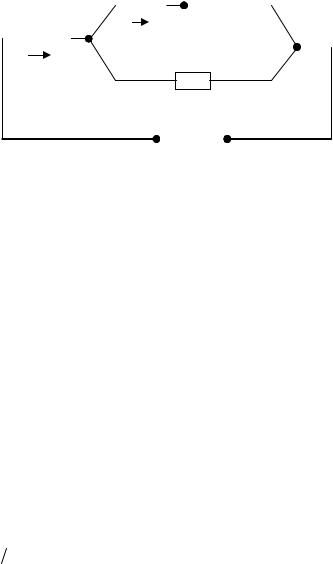
Для параллельных ветвей bcd и bd можно записать:

I1(2R + 3R) =I2·4R .

Отсюда I2 = 5/4 I1 . В то же время

I			I I		I		4				I		9		I ,					I		4			I						4 9					U									4 U					0
																																							0													,
	0		1	2	1		5				1		4		1						1	9					0				9 29 R 29 R
U			I 2R			4		U0				2R				8		U			,				U					I			R					9					U0			R							9	U	.
		2	1		29				R						29					0								1				0			29								R								29 0
На основании (2)													Uac				2		U		0		8			U				0			17		U				0
															29							29											29									17									.
Подставляя это выражение в (1), получим																																			q										CU				0
																																										29
			Пример 2. По проводнику сопротивлением R=3 Ом течет
ток, сила которого возрастает. Количество теплоты Q,
выделившееся в проводнике за время τ = 8с,																																											равно 200 Дж.

Определить количество электричества q, протекшее за это время по проводнику. В момент времени, принятый за начальный, сила тока в проводнике равна нулю.

Решение

Из условия равномерности возрастания тока следует I=kt

	или dq	dt kt , где k - коэффициент пропорциональности.
	Отсюда	dq = k·t·dt, a q			k 2
			k t dt			.
					2
			0
		27

Значение k найдем из выражения количества теплоты,

выделившейся в проводнике:

dQ = I2Rdt = k2 R t2 dt.

Интегрируя, получим Q k2R t2 dt 1k2 3R.

3

0

Отсюда k 3Q/( 3R) .

После подстановки получим

q

3Q / 4R 20 Кл .

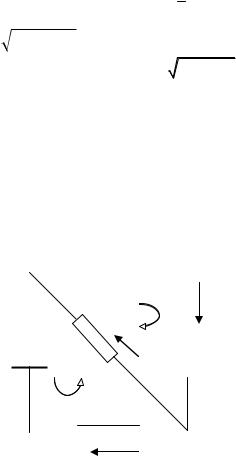
Пример 3. Найти силу тока во всех участках цепи, представленной на рисунке.(ξ1 =2,1 В, ξ2 = 1,9 В, R1 = 45 Ом, R2 = 10 Ом и Rз = 10 Ом). Внутренним сопротивлением элементов пренебречь.

Решение

Для расчета данной разветвленной цепи применим законы Кирхгофа.

			ξ1
А								B
						I1			I3
ξ2			R1						R3

R2

D C

I2

Для этого выберем направления токов в ветвях и покажем их стрелками на схеме. Узлы схемы обозначим точками А и С. Так как число узлов равно двум, то запишем одно уравнение по первому закону Кирхгофа, например, для узла С

I3=I1+I2 . (1)

28

Запишем второй закон Кирхгофа для контуров ABC и

ACD, выбрав направления обхода контуров.
I3R3	+ I1R1 = ξ1 ,	(2)
I1R1	- I2R2 = ξ2 .	(3)

Вместо контура ACD или ABC можно было взять контур

ABCD.

Имеем три уравнения с тремя неизвестными: I1, I2, I3. При решении этой системы уравнений целесообразно в уравнения подставить числовые коэффициенты. Тогда уравнения примут вид:

I3=I1+I2 10I3+45I1=2.1 45I1 – 10 I2=1.9

Решая эти уравнения, получим, I1=0,04A, I2 = -0,01 А, I3 = 0,03 А. Отрицательный знак у тока I2 указывает на то, что направление этого тока было выбрано нами неверно. В действительности ток I2 течет от D к С.

2.3.Задачи для выполнения контрольной работы №3

3.01.Четыре одинаковых точечных заряда q = 10 нКл

расположены в вершинах квадрата со стороной a = 10 см. Найти силу, действующую со стороны трех зарядов на четвертый.

3.02. Четыре одинаковых по модулю точечных заряда |q| =20 нКл, два из которых положительны, а два отрицательны, расположены в вершинах квадрата со стороной a = 20 см. Найти силу, действующую на помещенный в центр квадрата положительный точечный заряд Q =20 нКл.

29

3.03 Три одинаковых точечных заряда q=20.10-9Кл расположены в вершинах равностороннего треугольника. На каждый заряд действует сила F =10 мН. Найти длину a стороны треугольника.

3.04. Три одинаковых точечных заряда q = 9 нКл расположены в вершинах равностороннего треугольника. Какой точечный заряд q0 нужно поместить в центре треугольника, чтобы система находилась в равновесии?

3.05. Два положительных точечных заряда находятся на расстоянии 0,5 м один от другого. Один заряд вдвое больше другого. На прямой, их соединяющей, находится в равновесии заряженный шарик. Найти расстояние от этого шарика до большего заряда. Будет ли равновесие устойчивым?

3.06. Заряды q1 = 40 нКл и q2 = -10 нКл расположены на расстоянии r =10 см друг от друга. Какой надо взять третий заряд и где следует его поместить, чтобы система находилась в равновесии?

3.07. Два шарика массой m =0,1 г каждый подвешены в одной точке на нитях длиной l =20 см каждая. Получив одинаковые заряды, шарики разошлись так, что нити образовали между собой угол 2 = 60о. Найти заряд каждого шарика.

3.08. Два одинаковых заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол . Шарики погружаются в масло с плотностью о=8.102кг/м3. Определить диэлектрическую проницаемость масла, если угол расхождения нитей при погружении шариков в масло останется неизменным. Плотность материала шариков =1,6.103 кг/м3.

3.09. Два одинаковых шарика подвешены в воздухе на нитях так, что их поверхности соприкасаются. После того, как каждому шарику был сообщен заряд q=0,4мкКл, шарики разошлись на угол 2 = 60о. Найти массу шариков, если расстояние от центров шариков до точки подвеса l =0,2 м.

30