4.2. Вычисление собственных векторов и собственных значений матриц по методу данилевского

Очень простой и экономичный способ решения про­­блемы собственных значений был предложен в кон­це 30-х гг. А.М.Данилевским¹. Этот метод ос­но­ван на известном из ли­ней­ной алгебры факте [Кры­лов и др., 1972; Ку­рош, 1962], что подобные пре­об­ра­зования мат­ри­цыА не изменяют ее соб­ст­вен­ного мно­гочлена. В са­мом деле, еслиВ = S ^-1АS, то

|В - lЕ| = |S ^-1АS - lS ^-1ЕS| = |S ^-1| |А - lЕ| |S| = |А - lS| ,

по­этому, удачно подобрав матрицу подобия, мож­но при­вес­ти А к такой форме, что собственныймно­­­го­член бу­дет стро­ить­ся только по виду самой мат­­­ри­цы. А.М. Да­нилевский пред­­ложил при­во­дить ис­ход­ную мат­рицуАк ка­но­ни­чес­кой форме Фро­­бе­ни­уса

Ф=. (1.37)

Характеристический полином матрицы Фро­бе­ни­уса есть

|Ф - l Е| ==

= ... = (p₁ - l)(-l^n-1)- p₂ (-l^n-2) - ... - p_n-1l¹ - p _n =

= (-1)ⁿ P_n (l) .

Иными словами, элементы первой строки мат­ри­цыФро­бе­­ниуса (1.37) есть соответствующие ко­эф­фи­­ци­ен­ты ее соб­ственного многочлена (1.34). Ес­лиФпо­лу­чена из мат­ри­цыАподобными пре­об­ра­зо­ва­ни­­я­ми, то соб­ст­­вен­ный мно­гочлен мат­ри­цыАсов­па­да­ет с соб­ст­вен­ным мно­го­членом мат­рицыФ. Больше то­го ока­зы­ва­ет­ся, что най­ден­ная мат­­рица по­­добияSв выраженииФ = S^-1АS мо­­жет быть ис­поль­зо­­вана для на­хождения собст­вен­­ных век­­торов матрицыА[Кры­­лов и др., 1972].

Таким образом, основная задача сводится к отыс­­ка­нию мат­рицы подобия S. A.M. Данилевский в сво­ем ал­го­­рит­ме пред­­­­­ложил строить матрицуS, на­­­чи­ная процесс с последнейстро­ки. При этом по­сле­до­ва­тель­но, строка за стро­кой, ис­ход­­ная мат­рица приводится к форме Фро­бе­ни­у­са. Рас­смот­­рим эту вы­чис­ли­тельную схе­му.

Предположим, что элемент матрицы а_{n n-1} № 0 (если это не так, то прос­той перестaновкой столбцов можно всегда до­бить­ся вы­полнения условия),тогда разделим на не­гоn(n-1)-й столбец матрицыА. Полученный стол­бец умно­жим наа_ni и вычтем изi-го столбца. Про­делав эту процедуру дляi= 1, 2, ...,n-1,n, при­­ведем по­след­нюю строку к виду Фробениуса. Од­на­ко это рав­носильно умножению матрицыА на матрицуМ_n-1 вида

.(1.38)

Но чтобы выполнить пре­об­ра­зо­ва­ние по­до­бия, на­до матрицу Адомно­жить слева на матрицу (М_n-1) ^-1, ко­то­рая, как лег­ко убе­дить­ся, имеет вид

. (1.39)

Аналогично строится по­сле­до­ва­тель­ностьмат­риц

,

и ес­ли при этом все а_ii-1 № 0, то после n -1 шага ме­тода Да­­­ни­лев­­ско­го будем иметь

.

Если теперь обозначить

то равенство, полученное на n-1 шагe,может быть пре­д­­­став­­­ленов формеA^(Ф) = S ^-1 A S . Когдаис­ход­ная мат­­­рица А при­ведена к канонической фор­ме Фро­­бе­­ни­уса, то толь­ко по ви­ду пер­вой стро­ки мож­но вы­писать собственный мно­­­го­член мат­­рицы А.

Наши рассуждения относились к слу­­­чаю, когда все ко­эф­фициенты а_ii-1№0, который на­зы­ва­ет­сярегулярным. Рас­смот­­римне­регулярныйслу­чай.

Пред­положим, что про­цесс приведения Ак ви­ду Фро­­бе­ниуса доведен доk-й строки и вы­пол­не­ноn - k ша­­­гов пре­образований. Следующийn - k + 1 шаг не мо­жет быть вы­полнен, так как эле­мент а_kk-1равен нулю. Даль­нейшие дей­ствия зависят от су­щес­т­во­ва­ния в стро­кеk-го номера сле­ва от элемента с номером (k, k - 1) от­лич­но­го от нуля эле­мен­та. Пустьа_ki№0 при (i < k - 1). Тогда простой пе­ре­ста­новкой столбцов мож­но вновь перейти к ре­гу­ляр­но­му случаюTA^{(n - k)}, где

Легко убедиться, что ТА^(n-k) Тесть пре­об­ра­зо­ва­ние по­до­бия, так как (Т)² = Е; (Т)^-1 = Т.После это­го пре­об­ра­­зо­ва­­ния вычисления про­дол­жа­ют­ся, как и в ре­гу­ляр­ном слу­чае.

Более интересен случай, когда все элементы стро­ки k, ле­вееа_{kk -1} на (n-k) шаге равны нулю, т.е. не­воз­мож­но по­до­брать очередной элемент непре­об­ра­зо­ван­ной час­­ти стро­ки, на который будет вы­полняться деление.

Матрица, которая должна быть преобразована на оче­ред­ном шаге вычислительной схемы, условно де­лит­ся на че­тыре блока, причем в силу осо­бен­нос­тей стро­е­ния этой мат­рицы один из блоков будет сос­­то­ять ис­клю­­чительно из ну­левых членов, т.е. бу­дет нулевой мат­рицей О, второй бу­­дет мат­ри­цей Фро­бе­ни­у­саФ, а два ос­тав­ших­ся - обыч­ны­ми мат­рицами, ко­то­рые обо­зна­чимВиС(очевидно, что все матрицы рангаn - k):

=.

Тогда в силу теоремы Лапласа о разложении опре­де­лителя [Курош, 1962] имеет место ра­вен­с­т­во (в пра­вой части индексами обоз­на­че­ны по­ря­дки единичных мат­риц)

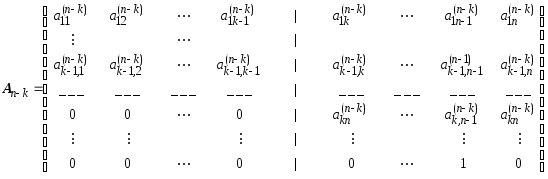|A^(n-k) - lE| = |B^(n-k)- lE_k-1| |Ф^(n-k) - lE_n-k+1|.

A так как Ф^(n-k)есть матрица Фробениуса, то ее ха­рак­те­рис­ти­чес­кий мно­го­член выписывается повиду первой стро­ки.Ос­та­ет­ся только привести B^(n-k) к ка­но­ни­чес­кому виду Фро­бениуса уже из­ло­жен­ным ме­то­дом.

Можно подсчитать, что в регулярном случае не­­об­хо­димо для вычисления ха­рак­те­рис­ти­чес­ко­го мно­го­чле­на вы­полнить n³действий, поэтому ме­тод Да­ни­лев­с­ко­го от­но­сят к самымэф­фек­тив­ным.

Для повышения точности вычислений на каж­дом ша­ге преобразований при помощи пе­ре­ста­нов­ки строк или стол­б­цов выбирают на­и­боль­ший эле­мент. Для конт­роля вы­чис­ле­ний на каж­дом ша­ге проверяют след мат­рицы, который не дол­жен изменяться.

Если найдены все собственные значения l_i мат­­рицыА и известна неособенная матрицаS, то в методе Да­ни­лев­­с­ко­го, как и в методе Кры­ло­ва, для определения соб­­ст­вен­ных значений ма­т­­­­­ри­­цыАможно обойтись без ре­­шения сис­темы од­но­­род­ных линейных алгебраичес­ких урав­не­нийA^(Ф)X = l_iX и использовать уже из­­­вест­ную мат­ри­цуS:

S = М _n-1 М _n-2 ... М₂ М₁. (1.40)

И хотя собственные значения матрицы A^(Ф)иАраз­лич­ны, они имеют одинаковый спектр[Ку­рош, 1962], сле­до­ва­тель­но, между соб­ствен­ны­ми значениями мат­ри­цыA^(Ф)иАсу­ществует связь, основанная на пре­об­ра­зовании подобия мат­­­риц [Курош, 1962]. Если векторXесть собст­вен­ный вектор матрицыA^(Ф), при­над­ле­жа­щий соб­ст­венному зна­че­ниюl_i, а вектор Y- собст­вен­ный вектор подобной ей мат­ри­цыФ = S^-1АS,при­над­ле­жа­щий тому же собственному зна­­че­ниюl_i, то векторSYтакже будет собственным век­то­­ром мат­pицыА, со­от­ветствующим собст­вен­ному зна­че­ниюl_i.

В этом утверждении можно легко убедиться. Пусть Y- собственный вектор матрицыФ, тогда

ФY = l Y ; S^-1АS Y = l Y ;

S S^-1АS Y = S l Y; АS Y = S l Y ;

АS Y = lS Y; A X = l X.

Таким образом, собственные векторы ис­ход­ной мат­ри­цы Алегко находятся по собственным зна­­че­ниям мат­рицы ФробениусаФY = lY или, за­­пи­­сав не­по­сред­ст­венно, по­лу­чим:

(1.41)

И так как собственный вектор определяется с точ­нос­тью до полиномного множителя, положим у_n =1. Тог­­да из системы (1.41) лег­ко найти векторY, а первое урав­­нение при этом используют иск­лю­­чительно для кон­троля вычислений. Век­торXматрицыАвы­чис­ля­ет­ся по формуле

X= SY = М _n-1 М _n-2 ... М₂ М₁ Y. (1.42)

Заметим, что не обязательно предварительно пе­ре­­мно­жать мат­рицы М, удобнее по­сле­до­ва­тель­но умно­­жатьYна М₁ , М₂, ...,М_n-1, при этом от умно­­жения на М_iу вектораY бу­дет из­ме­няться толь­коi-я координата.

Если же случай нерегулярный, то этим при­е­мом не­по­средственно пользоваться нельзя, на­­до пред­ва­ри­тель­­но вы­чис­лить матрицу S пол­нос­тью.

Подпрограмма Danil предназначена для вы­чис­ле­­­ния соб­­ственных значенийl_iматрицыА, по­ло­жи­тель­но оп­ре­­де­­ленной, эрмитовой по ме­то­ду Да­ни­лев­­ского. Соб­­ст­вен­ные значения l_iне упо­ря­до­чены по воз­рас­та­нию. Под­про­грам­маVectdпред­наз­на­че­на для вы­чис­ле­ния собст­вен­ных век­то­ровXмат­ри­цыA, со­от­вет­ст­ву­ю­щих соб­ст­вен­ным зна­чениямl_i. Век­торы за­пи­сы­ва­ют в столб­­цы мат­ри­цыХ, они так­­же не упо­ря­до­че­ны по воз­рас­­таниюl_i.

Вычислительный алгоритм подпрограммыDa­­nilсле­ду­­ющий:

1. Строится единичная матрица.

2. Определяется очередной номер строки (пос­лед­няя строка предыдущего пре­об­ра­зо­вания). Для пер­во­го ша­га iполагается равнымn, а далее умень­шается на еди­ни­цу с каж­дым шагом.

3. Формируется (i - 1)-я строка матрицыSкак ре­зуль­тат деленияа_ij/а_ij-1, гдеj- номер столбца,i- номер стро­ки (по фор­му­ле 1.40).

4. Формируется (i - 1)-я строка матрицыМ кака_ij(по формуле 1.38).

5. умножается Аслева наМ_i,справа наМ_i^-1, т.е.А_i =М_i^-1АМ.

6. формируется (i - 1)-я строка матрицыS (по фор­­му­ле 1.40) как (i - 1)-я строка матрицыМ(так как не ум­но­жается!).

7. Если i> 1, то повторить с шага 1.

8. Решаем характеристическое уравнение (мож­но воспользоваться программой из п. 4.1).

procedure Danil (const n:integer;

var a,m:mas1; var b: mas11);

type mas = array [1..N] of real;

mas1 = array [1..N] of mas;

var i, j, ns,nsp1, k : integer;

x : mas11; aij : real;

r, E, S, S1, A1 : mas1;

begin

for i := 1 to n do

{ ПРИСВОЕНИЕ НАЧАЛЬНЫХ ЗНАЧЕНИЙ}

for j := 1 to n do { МАССИВАМ }

begin

if i=j then

s[i,j] := 1

else

s[i,j] := 0.0;

if i=j then

m[i,j] := 1

else

m[i,j] := 0.0;

a1[i,j] := a[i,j];

end;

{ОПРЕДЕЛЕНИЕ ЕДИНИЧНОЙ МАТРИЦЫ}

ns := n- 1;

e:= s;

repeat

s := e;

NSP1 := NS + 1;

S1 := E;

for i := 1 to N do

S[NS,i] := -a1[NSP1,i] / a1[NSP1,NS];

S[NS,NS] := 1 / a1[NSP1,NS];

for i := 1 to n do

begin

m[ns,i] := s[ns,i];

s1[ns,i] := a1[nsp1,i];

end;

for i := 1 to N do

{ ФОРМИРОВАНИЕ МАТРИЦЫ А }

for j := 1 to N do

begin

Aij := 0.0;

for k := 1 to N do

Aij := Aij + a1[i,k] * S[k,j];

r[i,j] := Aij;

end;

for i := 1 to N do

for j := 1 to N do

begin

AIJ := 0.0;

for k := 1 to N do

Aij := Aij + S1[i,k]*r[K,J];

a1[i,j] := Aij;

end;

Dec (NS);

UNTIL NS = 0;

{ ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ВЕКТОРОВ }

for i := 2 to n+1 do

b[i] :=-a1 [1,i-1];

b[1] := 1.0;

lambda (4,0.0000001,b,x);

b := x;

end.

Формальные параметры про­цедуры. Входные:N (типin­teger) - размерность матрицыА, для ко­то­рой ищутся соб­­ственные значения l;А (типre­al) - мат­ри­­­цаА(ис­ход­ная) размером (n´n).Вы­ход­ные:А(типreal) - мат­ри­ца Фро­­­бе­ни­у­са;М (типre­al) - мас­сив, содержащий стро­ки, от­лич­ные от ну­­ля и еди­ни­цы мат­рицы пре­об­ра­зо­ванийМ_n-1;В (типreal) - мас­­сив собственных зна­че­ний мат­рицыА.Про­­це­ду­­раDanil в работе об­ра­ща­ет­ся к под­про­грам­меLam­bda, описанной в п. 4.1.

Вычислительный алгоритм процедуры Vect:

1. Вычисляется вспомогательный вектор Y, со­­­от­­ветствующий oчередному значениюl (по фор­му­ле 1.41).

2. Вычисляется собственный вектор мат­ри­цы Аи заносится в соответствующий стол­бец мас­си­­­ваV (по формуле 1.42).

3. Если выбраны не все значения l, то пе­ре­ход на шаг 1, иначе - конец подпрограммы.

procedure Vect (const n: integer; x: mas11;

m:mas1; var v : mas1);

type mas = array [1..n] of real;

var y : mas; i,j, k, NS : integer; sum : real;

begin

NS := 1;

repeat

y[n] := 1;

for i := n-1 downto 1 do

y[i] := y[i+1]*x[ns];

for i := 1 to n do

begin

sum := 0.0;

for j := 1 to n do

sum := sum + m[i,j]*y[j];

y[i] := sum;

end;

for i := 1 to n do

v[i,ns] := y[i];

Inc (ns);

until ns>n;

end.

Формальные параметры про­цедуры.Входные:М1 (типinteger) - начальный номер собст­вен­ного зна­­­чения lматрицы А, начиная с ко­то­ро­го надо ис­кать соб­ст­вен­ные векторы матрицы А;М2 (типin­te­­ger) - по­след­ний номер собственного значенияlмат­­рицыА,до ко­то­рого надо искать собст­вен­ные ве­к­торы (очевидно, чтоМ1 < М2);М(типre­al) - вспо­­мо­га­тельный массив, содержащий стро­ки мат­ри­цы пре­об­разованийМ,ис­поль­зуемый для пе­ре­сче­та собст­венного вектора мат­ри­цы Фро­бениуса в соб­ст­венный вектор матрицы А;В(типreal) - мас­сив собст­венных значений мат­ри­цыА.Вы­ходные:V (типreal) - массив собст­вен­ных векторов мат­рицыА. Если определяются не всеl, то собственные век­­то­ры рас­по­лагаются сМ1 поМ2 столбец, а ос­таль­­­ные значения мас­си­ваVне определены.

Примечание. В процедуреVectот­сут­ству­ет конт­роль вы­числений собственных значений.

Для проверки работы программы (см. табл. 1.19) собст­вен­ные значения и соб­ст­венные векторы мат­рицы, взятой из п. 4.1, на­хо­дятся с точностью до 0.0001. Все про­­­ме­жуточные мат­ри­цы для конт­ро­ля за работой про­грам­мы выписаны.

Таблица 1.19

	Номер элемента
Параметр	[ 1 ]	[ 2 ]	[ 3 ]	[ 4 ]
	Итерация первая
Матрица	0.533333	-1.416667	1.833333	-0.140000
А	-0.310000	-3.470000	4.500000	0.260000
	-0.221133	-3.097133	4.146667	0.166800
	0.000000	0.000000	1.000000	0.000000
Матрица	1.000000	0.000000	0.000000	0.000000
(М3)^-1	0.000000	1.000000	0.000000	0.000000
	0.080000	0.080000	0.060000	0.120000
	0.000000	0.000000	0.000000	1.000000
Матрица	1.000000	0.000000	0.000000	0.000000
М3	0.000000	1.000000	0.000000	0.000000
	-1.333333	-13.333333	16.666667	-2.000000
	0.000000	0.000000	0.000000	1.000000
	Итерация вторая
Матрица	0.634482	0.457412	-0.063403	-0.2162961
А	0.052473	0.575518	0.632654	-0.178628
	0.000000	1.000000	0.000000	0.000000
	0.000000	0.000000	1.000000	0.000000
	1.000000	0.000000	0.000000	0.000000
Матрица	-0.221133	-3.097133	4.146667	0.166800
(М2)^-1	0.000000	0.000000	1.000000	0.000000
	0.000000	0.000000	0.000000	1.000000
Матрица	1.000000	0.000000	0.000000	0.000000
М2	-0.071399	-0.322879	1.338873	0.053856
	0.000000	0.000000	1.000000	0.000000
	0.000000	0.000000	0.000000	1.000000
	Итерация третья
Матрица	1.210000	0.291500	-0.583363	0.101987
А	1.000000	0.000000	0.000000	0.000000
	0.000000	1.000000	0.000000	0.000000
	0.000000	0.000000	1.000000	0.000000

Окончание таблицы 1.19

	Номер элемента
Параметр	[ 1 ]	[ 2 ]	[ 3 ]	[ 4 ]
Матрица	0.052473	0.575518	0.632654	-0.178628
(М1)^-1	0.000000	1.000000	0.000000	0.000000
	0.000000	0.000000	1.000000	0.000000
	0.000000	0.000000	0.000000	1.000000
Матрица	19.057255	-10.967785	-12.056645	3.404166
М1	0.000000	1.000000	0.000000	0.000000
	0.000000	0.000000	1.000000	0.000000
	0.000000	0.000000	0.000000	1.000000
Собственные	0.214779	-0.699093	1.043229	0.651085
значения матрицы А
	0.497526	-0.038678	0.526914	-3.835256
Собственные	0.291000	-1.037180	1.061588	1.062538
векторы матрицы А	-2.963725	0.229082	0.530102	-0.202091
(не нормированные)	1.000000	1.000000	1.000000	1.000000
	-0.167872	0.037291	0.496345	1.000000
Собственные	-0.098187	1.000000	1.000000	-0.277045
векторы матрицы А	1.000000	-0.220871	0.499348	0.052693
(нормированные)	-0.337413	-0.964153	0.941985	-0.260739