1.2. Комбинаторика. Бином ньютона и родственные формулы
Число перестановокизnэлементов определяется формулой
Pn = n! ; (1.2)
число размещенийиз nэлементов поmэлементов
; (1.3)
число сочетанийизnэлементов по mэлементов
.
(1.4)
Число перестановок с повторениями (кортежами) состава(спецификации) (k1, k2, ..., kr ) определяется формулой
;
(1.5)
число сочетанийизn элементов поm сповторениями
.
(1.6)
При численных расчетах также можно использовать рекуррентную формулу
. (1.7)
В формулах (1.2) - (1.4) n!, m!,k! и (n-m)! - факториалы, которые легко могут быть вычислены из определения
0! = 1,
n > 0. (1.8)
Однако для больших nиспользование выражения (1.8)в связи сo значительным количеством операций умножения чисел с плавающей точкой приводит к неоправданнымзатратам процессорного времени. В таких случаях для приближенного вычисления факториалов удобно использоватьасимптотическое разложение Стирлинга, в результате получаемформулу Стирлингадляn!:
приn ®¥. (1.9)
Относительная ошибка формулы
Стирлинга, как это видно из выражения
(1.9), убывает с возрастанием
n. Для достаточно большихn
,
однако, более точного
результата можно добиться,
если использовать специальную
формулу [Корн, Корн, 1978]:
,
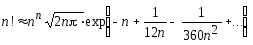(1.10)
поскольку
;
приn ®¥.
Отмеченные особенности
учтены нами в процедуре вычисления
факториала, которая может
быть с успехом использована для
нахождения
в соответствии с формулами
(1.2) - (1.6).
Формальные параметры процедуры.Входные:n(типinteger) - натуральное число, факториал которого требуется вычислить;k (типinteger) - ключ, значение которого отвечает выбору одной из формул (1.8) - (1.10):k < 0 - формула (1.8), k = 0 - формула (1.9),k > 0 -формула (1.10).Выходной: идентификатор процедуры-функции fct(типreal)- значение факториала.
{*** fct ***}
Function fct (n, k : integer) : real;
const pi = 3.14159265;
var s1, s2, s3 : real; i : integer;
begin
if n=0 then
begin
fct:=1;
exit;
end;
if k < 0 then
begin
fct:=1;
for i:=1 to n do
fct:=fct*i;
exit;
end;
s1:=sqrt(2*pi*n);
if k=0 then
begin
s3:=0;
s2:=0
end
else
begin
s3:=1/(360*n*n*n);
s2:=1/(12*n)
end;
fct:=exp(n*ln(n))*s1*exp(-n+s2-s3);
end .
Оценка точности вычислений проводилась при тестировании программы для n = 5, 10, 15, 20, 30; k =-1, 0, 1. Результаты, полученные приn = 5, 10, 15, и соответствующие им величины относительной погрешности представлены в табл.1.2.
Результаты тестирования показывают, что с ростом nпогрешность вычисленияn! уменьшается, причем во всех случаях формула (1.10) дает более точный результат. Однако следует отметить, что при дальнейшем увеличенииnпогрешность формулы (1.10) остается практически на том же уровне (~1.0e - 5 %) и при необходимости получить более точный результат требуется удержать следующий член в разложении (1.10). Дальнейший рост nприводит к появлению ошибок округления, связанных с конечностью разрядной сетки ЭВМ.
Таблица 1.2
-
n
Формула (1.8) (точное значение)
Формула (1.9)
Формула (1.10)
5
120
118.019172668 (1.65 %)
119.9999771 (1.9 e - 5 %)
10
3628800
3598695.75 (0.82 %)
3628800 (0 %)
15
1307674279936
1300430716928 (0.55 %)
1307674411008 (1.0 e - 5 %)
Процедура fctможет быть эффективно использована при вычислении бинома Ньютона:
(1.11)
и величины полинома
,
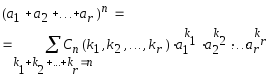(1.12)
где суммирование проводится по всем наборам неотрицательных целых чисел (k1 ,k2 ,...,kr ),для которыхk1 + k2 + +... + kr = n.При этомCn (k1, k2, ..., kr),вычисляемые по формуле (1.5), называются полиномиальными коэффициентами.Формула для определения количества полиномиальных коэффициентов имеет вид:
.
Рассмотрим процедуру-функцию вычисления бинома Ньютона, в которой используется функция fctв соответствии с формулой (1.11).
Формальные параметры процедуры.Входные:a,b (типreal)- значения слагаемых aиbв выражении (1.11);n(типinteger) - показатель степени бинома;k(типinteger) - ключ, определяющий выбор алгоритма вычисления факториала (см. описание параметров процедуры-функции fct). Выходной:функция binn(типreal) - значение бинома Ньютона.
Function binn (var a, b : real;
var n, k : integer;): real;
var s,f1,f2,f3 : real; l,m : integer;
begin
bin:=0;
f1:=fct(n,k);
for l:=0 to n do
begin
f2:=fct(l,k);
m :=n-l;
f3:=fct(m,k);
s :=f1/(f2*f3);
bin:=bin+s*exp(a*ln(m)+b*ln(l));
end;
end; {*** binn ***} .
Оценка точности вычислений бинома проводилась при тестировании программы для n = 5, 10, 15, 20, 30; k =- 1 (данное значениеk соответствуетточному вычислению факториала в процедуре-функцииfct) и различных параметровa иb. Результаты, полученные приn =5, 7, 10, 15; a = =1.5; b = 2.5, -2.5, исоответствующие им величины относительнойпогрешности представлены в табл. 1.3.
Таблица 1.3
|
Параметр |
Значение бинома при использовании формулы | ||||||
|
n |
a |
b |
(1.8) |
(1.10) | |||
|
5
7
10
15
|
1.5
1.5
1.5
1.5
|
2.5 - 2.5 2.5 - 2.5 2.5 - 2.5 2.5 - 2.5 |
1024 (+ 0%) — 1 (+ 0%) 16384 (+ 0%) — 1 (+ 0%) 1048576 (+ 0%) 1.00098 (+9.766e-2%) 21073741696 (+1.2e-5%) — |
1024.1940 (+1.89e-2%) — 0.8770 (+11.3%) 16385.5449 (+9.4e-3%) 0.125 (+112.6%) 1048610 (+3.2e-3%) — 1073747328 (+5.1e-4%) — |
| ||
Из таблицы видно, что при b > 0 с увеличениемnточность вычислений растет и практически ограничена только ошибками округления, для отрицательных же bуже приn>10 в случае использования формулы (1.8) и приn ~ 5 в случае использования формулы (1.10) для факториала погрешность резко возрастает, что связано с вычитанием больших чисел в правой части равенства (1.11). Поэтому приb < 0 рекомендуется использовать элементарную формулу (a + b)n, на современных быстродействующих ЭВМ это даст некоторый выигрыш во времени счета.
Заметим, что совершенно аналогично может бытьпостроена процедура вычисления величины полинома (1.12), поэтому она здесь не приводится.
Когда известно некоторое сочетание из nпоm, тогда вычисление следующего по порядку сочетания мо-
жет быть эффективно осуществлено с помощью процедуры генератора сочетаний [Агеев и др., 1976], которая образует следующее по порядку сочетание из n целых чисел по m, если заданы n, m и предшествующее сочетание.
Формальные параметры процедуры.Входные:n, m(типinteger); векторj [1:m] (типinteger) - предшествующее сочетание.Выходной:тот же векторj, в котором целые числа меняются от 0 доn - 1 и всегда при входе и выходе из процедуры составляют монотонную строго возрастающую последовательность. Если входной векторj состоит из нулей, то в качестве первого сочетания будет получено (n - m, ..., n - 1).Такое же сочетание получится и после сочетания (0, 1,..., k - 1),являющегося последним значением вектора jв этом цикле.
procedure comb (n, m : integer; var j : mas1);
var a, b, l : integer;
begin
for b:= 1 to m do
if j[b]>b then
begin
a:=j[b]-b-1;
for l:=1 to b do j[l]:=l+a;
exit;
end;
b:=n-m-1;
for l:=1 to k do
j[l]:=b+l;
end; {*** comb ***}.
Данный алгоритм был переведен авторами с языка ALGOL на языкPASCALи проверен на машине IBM PC/AT-286 для тех же значений входных параметров, что и в работе Агеева и др. (1976),n = 4, k = 3. В качестве начального вектора jбыл выбран вектор (0,0,0). В результате последовательных обращений к процедуре получены следующие сочетания: (1,2,3), (0,2,3), (0,1,3), (0,1,2), что полностью соответствует результатам тестированияALGOL-программы, приведенными в работе Агеева и др. (1976).