
Qiao S.Principles of floating point computation
.pdfCAS727, S. Qiao |
Part 1 Page 1 |
Principles of Floating Point
Computation
Before investigating numerical software engineering, we must research the principles of finite precision computing.
1Floating-point Number System
is a subset of the real numbers |
||
A floating point number system F R |
− |
|
whose elements have tthe form y = ±m ×βe |
|
t. The mantissa m is an integer |
satisfying 0 ≤ m ≤ β −1.−To ensure a unique representation for each y F |
||
it is assumed that m ≥ βt 1 if y 6= 0, so that the system is normalized. Note |
||
that an alternative way of expressing y is y = ±βe × .d1d2...dt where each digit di satisfies 0 ≤ di ≤ β − 1. It is important to realize that the floating point numbers are not equally spaced. The system F is characterized by four integer parameters: the base β (also called radix); the precision t; and the exponent range emin ≤ e ≤ emax. Another measure of the precision is called machine precision denoted by M . It is defined as the distance between 1.0 and the next larger floating point number. Clearly, M = β1−t.
Example 1 When β = 2, t = 3, emin = −2 and emax = 3 there are 24 normalized positive floating point numbers:
−2 |
1.01 × 2 |
−2 |
−2 |
−2 |
|
1.00 × 2− |
1 |
|
1.10 × 2 |
1.11 × 2 |
|
1.00 × 2 |
· · · |
|
1.10 × 23 |
1.11 × 23 |
|
Figure 1 shows some of the positive floating-point numbers in our small system. Note that they are not equally spaced.
2Underflow and Overflow
Overflow means that the exponent is too large to be represented in the exponent field. Underflow means that the exponent is too small to be represented in the exponent field. In our small floating point system, the largest normal number Nmax is 1.11 × 23, which is called the overflow threshold. When the result is larger than Nmax overflow occurs. The smallest positive normal number Nmin is 1.00 × 2−2, which is called the underflow threshold. When the result is smaller than Nmin underflow occurs. We use the above Example 1 to illustrate overflow and underflow.

CAS727, S. Qiao |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Part 1 Page 2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1/4 |
1/2 |
1 |
2 |
12 |
14 |
|
|||||||||||||||||||||||
Figure 1: A small floating-point number system.
Example 2 Using the system in Example 1, When a = 1.00 × 21 and b = 1.10 × 23, then a/b causes underflow and a b causes overflow.
3IEEE Standard
The IEEE standard 754 [5], published in 1985, defines a binary floating point arithmetic system. Among the design principles of the standard are:
•encourage software developers to develop robust, e cient, and portable numerical programs,
•enable the handling of arithmetic exceptions,
•provide for the development of transcendental functions and very high precision arithmetic.
For recent status on the IEEE standard see [6]. This section provides a tour of the IEEE standard. Each subsection discusses one aspect of the standard.
Before going into the IEEE floating-point number system, we use the small number system in Example 1 to illustrate floating-point number representation.
In Example 1, all normalized numbers have a leading bit 1. So, we can save this bit, called hidden bit. Thus we need two bits for the fraction, three bits for the exponent, and one bit for the sign, a total of six bits. We define our small floating-point number system as follows.
Definition 1
A Small Floating-Point Number System
t |
emax |
emin |
Exponent width in bits |
Format width in bits |
3 |
+3 |
−2 |
3 |
6 |
This small floating-point number system can represent 24 positive numbers and 24 negative numbers.
CAS727, S. Qiao |
Part 1 Page 3 |
3.1Formats
Base (Radix)
In IEEE standard 754, the base is 2.
Precision
The IEEE standard defines four di erent precisions: single, double, singleextended, and double-extended. In 754, single and double precision correspond roughly to what most floating-point hardware provides. Single precision occupies a single 32 bit word, double precision two consecutive 32 bit words. Extended precision is a format that o ers at least a little extra precision and exponent range. The IEEE standard only specifies a lower bound on how many extra bits extended precision provides. The minimum allowable double-extended format is sometimes referred to as 80-bit format, even though Table 1 shows it using 79 bits. The reason is that hardware implementations of extended precision normally do not use a hidden bit, and so would use 80 rather than 79 bits. This feature is available on almost all architectures. But it continues to be under-untilized for lack of linguistic support because the programming language community appears not to understand how and why this format is intended to be used. Long double is intended to support double and single the way double supports single. So, intermediate results in evaluating an expression are computed in high precision. Why? Extra-precise arithmetic attenuates the risk of error due to roundo .
Example 3 Extra precision as a way to conserve interest rate’s monotonicity [7, p. 64]. An important requirement for certain financial computation of rates of return is monotonicity. If a small change in data causes a computed result to change, its change should not go in the wrong direction. For example, if return on an investment is increased, its computed rate of return must not decrease. The conservation of monotonicity becomes more challenging as it becomes more important during computations designed to optimize rates of return. These rates satisfy equations that can have more than one root, and the choice of the right root can be spoiled if monotonicity is lost to round o . By far the easiest way to conserve monotonicity is to compute extra precisely.
Exponent
Since the exponent can be positive or negative, some method must be chosen to represent its sign. Two common methods of representing signed numbers

CAS727, S. Qiao |
|
|
|
Part 1 Page 4 |
||
|
|
|
|
|
|
|
|
|
|
|
Extended |
|
|
|
|
|
|
|
|
|
|
Parameter |
Single |
Double |
Single |
Double |
|
|
|
|
|
|
|
|
|
t |
24 |
53 |
≥ 32 |
≥ 64 |
|
|
emax |
+127 |
+1023 |
≥ +1023 |
> +16383 |
|
|
emin |
−126 |
−1022 |
≤ −1022 |
≤ −16382 |
|
|
Exponent width in bits |
8 |
11 |
≥ 11 |
≥ 15 |
|
|
Format width in bits |
32 |
64 |
≥ 43 |
≥ 79 |
|
Table 1: IEEE 754 Format Parameters
are sign/magnitude and two’s complement. The IEEE binary standard does not use either of these methods to represent the exponent, but instead uses a biased representation for e cient calculation of exponents. In the case of single precision, where the exponent is stored in 8 bits, the bias is 127 (for double precision it is 1023). What this means is that if k is the value of the exponent bits interpreted as an unsigned integer (biased), then the exponent of the floating-point number is k − 127 (unbiased).
Example 4 In our small floating-point number system (Definition 1), the bias is 3. Thus, for example, the unsigned integer (binary) 001 in the exponent field (biased) represents exponent −2 (unbiased), which is emin.
3.2Special Quantities
The IEEE standard specifies the following special values: ±0, NaNs, ±∞, and denormalized numbers. These special values are all encoded with exponents of either emax + 1 or emin − 1.
Signed Zeros
Zero is represented by the exponent emin − 1 and a zero fraction. Since the sign bit can take on two di erent values, there are two zeros, +0 and −0. The IEEE standard defines comparison so that +0 = −0, rather than −0 < +0. Although it would be possible always to ignore the sign of zero, the IEEE standard does not do so. When a multiplication or division involves a signed zero, the usual sign rules apply in computing the sign of the answer.
NaNs |
√ |
|
Traditionally, the computation of 0/0 or −1 has been treated as an unrecoverable error which causes a computation to halt. However it makes sense for a computation to continue in such a situation.

CAS727, S. Qiao |
|
Part 1 Page 5 |
|
|
|
|
|
|
Operation |
NaN Produced By |
|
|
|
|
|
|
|
|
|
|
+ |
∞ + (−∞) |
|
|
|
0 ∞ |
|
|
/ |
0/0, ∞/∞ |
|
|
REM |
x REM 0, ∞ REM y |
|
|
sqrt |
sqrt(x) when x < 0 |
|
|
|
|
|
Table 2: Operations that Produce a NaN
Example 5 Suppose there is a statement of return (−b + SQRT(d))/(2 a) in a program. If d < 0, then SQRT(d) is a NaN. In IEEE standard if a
NaN involves a floating point computation, the result is another NaN. So the return value of (−b + SQRT(d))/(2 a) is NaN, which indicates that it is not a real number. The computation continues.
In IEEE 754, NaNs are often represented as floating point numbers with exponent emax + 1 and nonzero fractions. Implementations are free to put system-dependent information into the fraction. Thus there is not a unique NaN, but rather a whole family of NaNs. In general, whenever a NaN participates in a floating point operation, the result is another NaN.
Infinities
The infinity symbol is represented by a zero fraction and the same exponent field as a NaN (emax +1); the sign bit distinguishes between ±∞. The infinity symbol obeys the usual mathematical conventions regarding infinity, such as ∞ + ∞ = ∞, (−1) ∞ = −∞, and (finite)/∞ = 0.
Just as NaNs provide a way to continue a computation when expressions
√
like 0/0 or −1 are encountered, infinities provide a way to continue when an overflow occurs. This is much safer than simply returning the largest representable number.
|
√ |
|
|
|
Example 6 Suppose that there is a computation of |
|
2 |
under our small |
|
x |
|
|||
floating-point number system (Definition 1). If x |
= 1.00 × 23, then x2 |
|||
overflows. If it is replaced by the largest number 1.11 ×23, then the result of
√
x2 is 1.00 × 22 rather than 1.00 × 23. Obviously it is far from our expected result. Adopting the IEEE standard, the result of x2 would be ∞. So the final result of this computation would be ∞. It is safer than just returning an ordinary floating point number which is far from the correct answer.
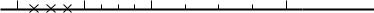
CAS727, S. Qiao |
|
|
Part 1 Page 6 |
0 |
1/4 |
1/2 |
1 |
Figure 2: Denormalized numbers (between 0 and 2−2 marked by ×).
Denormalized Numbers
The IEEE standard uses denormalized numbers, which guarantee x = y x − y = 0, as well as other useful relations. Specifically, if the bits in the fraction field are b1, b2, ..., bp−1, and the value of the exponent is e, then when e > emin −1, the number being represented is 1.b1b2...bp−1 ×2e whereas when e = emin − 1, the number being represented is 0.b1b2... × 2e+1. The +1 in the exponent is needed because denormals have an exponent of emin, not
emin − 1.
Example 7 In our small floating-point systm (Definition 1) if normalized numbers x = 1.01 × 2−2 and y = 1.00 × 2−2, then x − y is too small to be represented in normalized number range and must be flushed to zero (underflow), although x =6 y. When the denormalized number is introduced, x − y does not underflow, instead x − y = 0.01 × 2−2. This behavior is called gradual underflow (sometimes called graceful underflow). Figure 2 plots the positive denormalized numbers in our small floating point number system.
When denormalized numbers are added to the number line, the spacing between adjacent floating point numbers varies in a regular way: adjacent spacings are either the same length or di er by a factor of β. Without denormals, the spacing abruptly changes from β−t+1βemin to βemin , which is a factor of βt−1, rather than the orderly change by a factor of β. Because of this, many algorithms that can have large relative error for normalized numbers close to the underflow threshold are well-behaved in this range when gradual underflow is used.
Table 3 summarizes IEEE values.
3.3Correctly Rounded Operations
When we apply a floating point operation, say add, to floating point numbers, the exact result may not fit the format of the destination. For example, consider in our small system c = a+b where a = 1.00×20 and b = 1.01×2−2 . The exact result is 1.01012 , which does not fit the format of the destination c, a floating point number in our system. We must round the exact result to
CAS727, S. Qiao |
|
|
Part 1 Page 7 |
|
|
|
|
|
|
|
Exponent |
Fraction |
Represents |
|
|
|
|
|
|
|
|
|
|
|
|
e = emin − 1 |
f = 0 |
±0 |
|
|
e = emin − 1 |
f 6= 0 |
0.f × 2emin |
|
|
emin ≤ e ≤ emax |
− |
1.f × 2e |
|
|
e = emax + 1 |
f = 0 |
∞ |
|
|
e = emax + 1 |
f 6= 0 |
NaN |
|
Table 3: IEEE 754 values
fit the format of our system. For example, the floating point number that is nearest to 1.01012 is 1.01 × 20.
The IEEE standard requires that the following floating point operations are correctly rounded:
•arithmetic operations +, −, , and /
•square root and remainder
•conversions of formats
Correctly rounded means that result must be the same as if it were computed exactly and then rounded, usually to the nearest floating-point number. We will discuss the rounding modes in the next section.
The format conversions include:
•between floating point formats, e.g., from single to double.
•between floating point and integer formats.
•from floating point to integer value (not format).
•between binary and decimal.
3.4Rounding Modes
In the IEEE standard, rounding occurs whenever an operation has a result that is not exact. By default, rounding means round toward nearest. The standard requires that three other rounding modes be provided, namely round toward 0, round toward +∞, and round toward −∞.
1.Round to +∞: always round up to the first representable floating point number.
CAS727, S. Qiao |
|
|
|
Part 1 Page 8 |
||
|
|
|
|
|
|
|
|
Round |
→ +∞ |
→ −∞ |
→ 0 |
→ nearest |
|
|
1.1001 × 22 |
1.11 × 22 |
1.10 × 22 |
1.10 × 22 |
1.10 × 22 |
|
Table 4: Four rounding modes
2.Round to −∞: always round down to the first representable floating point number.
3.Round to 0: always truncate the digits that after the last representable digit.
4.Round to nearest even: always round to the nearest floating point number. In the case of a tie, the one with its least significant bit equal to zero is chosen.
Example 8 There are two floating point numbers: a = b = 1.01 × 21 under our small floating-point number system. The exact value of a b = 1.1001 × 22. This value is between 1.10 × 22 and 1.11 × 22. Table 4 illustrates the rounded value under di erent rounding modes.
Why dynamic directed rounding modes? Testing numerical stability. How? Di erent rounding introduces slightly di erent rounding errors. If slightly perturbed intermediate results cause significant changes in the final results, the program is unstable.
Example 9 Computing the area of a needle-like triangle and testing instability using di erent rounding. See [7, p. 58]
Another application of dynamic directed rounding modes is interval arithmetic.
3.5Exceptions, Flags and Trap Handlers
The IEEE standard divides exceptions into 5 classes: overflow, underflow, division by zero, and invalid operation and inexact as shown in Table 5. They are called “exceptions” because to any policy for handling them, imposed in advance upon all programmers by the computer system, some programmers will have good reasons to take exception. IEEE 754 specifies a default policy for each exception, and allows system implementor the option of offering programmers an alternative policy, which is to trap with specified information about the exception to a programmer-selected trap-handler.
CAS727, S. Qiao |
|
Part 1 Page 9 |
|||
|
|
|
|
|
|
|
Exception |
|
Result when traps disabled |
Argument to trap handler |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
overflow |
|
±∞ or ±xmax |
round(x2−α) |
|
|
underflow |
|
0, ±2emin or denormal |
round(x2α) |
|
|
divide by zero |
|
∞ |
operands |
|
|
invalid |
|
NaN |
operands |
|
|
|
|
|
|
|
|
inexact |
|
round(x) |
round(x) |
|
|
|
|
|
|
|
Table 5: Exceptions in IEEE 754
The IEEE standard has a number of flags. A flag is a type of global variable raised as a side-e ect of exceptional floating-point operations. There is one status flag for each of the five exceptions: underflow, overflow, division by zero, invalid operation and inexact; and four rounding modes. When any exception occurs, a status flag is also set. Also it can be sensed, saved, restored and lowered by a program. Implementations of the IEEE standard are required to provide users with a way to read and write the status flags. The flags are “sticky” in that once set, they remain set until explicitly cleared. These modes and flags can be put to good use.
IEEE 754 specifies a default policy for each of floating-point exceptions:
1.Signal the event by raising an appropriate one of the five flags, if it has not already been raised.
2.(Pre)substitute a default value for what would have been the result of the exceptional operation, see Table 5.
3.Resume execution of the program as if nothing exceptional had occurred.
The default policy is a reasonable thing to do. For example, if we compute the resistance of two parallel resistors R1 and R2, the total resistance is 1/(1/R1 + 1/R2). With the default values, when R1 or R2 or both equals zero, the result is zero. Without default values, we would have to check conditions. Conditional branches are ine cient on pipeline machines.
With these default values, IEEE 754’s floating-point becomes an algebraically completed system: this means the computer’s every algebraic operation produces a well-defined result for all operands.
Why should computer arithmetic be algebraically completed?
Otherwise some exceptions would have to trap. Then robust programs could avert loss of control only by precluding those exceptions (at the cost of time

CAS727, S. Qiao |
Part 1 Page 10 |
wasted pretesting operands to detect rare hazards) or else by anticipating them all and providing handlers for their traps.
Example 10 A Tale of the Ariane 5, [7, p. 22]. A European satellite-lifting rocket turned cartwheels due to the incompleted system. Strong acceleration upon launch caused conversion to integer overflow in the software. Lacking a handler for this unanticipated overflow trap, this software trapped to system. This was misinterpreted as necessitating strong corrective action.
It is not the only useful way to algebraically complete the real and complex number systems. There are other possible ways. By majority vote a committee chose the particular completion specified by IEEE 754 because it was deemed less strange than others and more likely to render exceptions ignorable.
What’s wrong with the default values specified for these exceptions by IEEE 754? For example,
x2 + 1 |
x > pβ βemax /2 |
||
x |
|
|
|
then x2 overflows and the result is zero, obviously wrong. Although, in this case we can rewrite the formula:
1
x + 1/x
this is not always possible in general.
A programmer can have good reasons to take exception to that completion and to every other since they jeopardize cancellation laws or other relationships usually taken for granted. For example, x/x =6 1 if x is 0 or not finite; x − x =6 0 =6 0 · x, if x is not finite. After non-finite values have been created they may invalidate the logic underlying subsequent computation and then disappear: (finite/Overflow) becomes 0, (NaN < 7) becomes false,
.... Perhaps no traces will be left to arouse suspicions that plausible final results are actually quite wrong. For example,
do
S
until (x ≥ 100)
If x ever becomes NaN, x ≥ 100 results in false and NaN disappers without traces. Another example of trap handlers is backward compatibility. Old
