Dresner, Stability of superconductors.2002

120

CHAPTER 6

(6.11.3)

give an upper bound to the solutions of Eq. (6.11.2) that obey the same boundary and initial conditions. Equation (6.11.3) is linear and has the infinite-medium point-source kernel

(4pt)–1/2exp(–z2/4t + t)

(6.11.4)

If the initial value of finite interval, say 0 ≥

the temperature rise T – 1 (call it DT(z,0)) is > 0 only on a z ≥ c, then for z < 0,

(6.11.5a)

(6.11.5b)

The right-hand side of Eq. (6.11.5b) is then an upper bound to T2 – 1, where T2 is the solution of Eq. (6.11.2).

The locus of a constant value K of the right-hand side of Eq. (6.11.5b) is given

by

(6.11.6)

As t grows large, this locus asymptotically becomes the locus z2 = 4t2 or z = –2t (remember, we are considering the leftward propagating edge of the normal zone).

Let us switch to a frame of reference traveling to the left with a velocity –2 by introducing the new variable z´ = z + 2t. Then in the z´-frame,

(6.11.7)

for z´ < 2t (i.e, z < 0). Shown in Fig. 6.12 is a sketch of the right-hand side of Eq. (6.11.7) in the z´-frame. For l z´l << 4t, the profile is close to ez´ , whereas for z´ < –4t, the profile drops more rapidly than a simple exponential. The arrows show the direction of migration of the profile and the various boundaries as time advances. Shown also as a dashed curve is the profile of the traveling-wave solution of Section 6.10 corresponding to a velocity v > 2.

A contradiction is evident in this diagram. Since the traveling-wave solution is given by s = v(T – 1) when T < Tc,

Uncooled Conductors

121

Figure 6.12. A sketch of the right-hand side of Eq. (6.11.7).

T– 1 ~ exp[v(z + vt)] = exp[vz´ + (v – 2)t]

(6.11.8)

Thus at any fixed instant of time, the traveling-wave solution falls exponentially as

z´	– , whereas T1 falls as a Gaussian function as z´	– . Thus T1 cannot be
	8	8

larger than T everywhere. Therefore, an initial condition that is confined to a finite interval cannot asymptotically mature into a traveling wave.

If this contradiction were all the trouble created by the analysis we have just completed, it would not be so serious because the departure of the true solution from the traveling-wave solution only occurs in the remote wings of the propagating front where the temperaturerise is very small. Furthermore, this situation gets better as time goes on. But unfortunately there is more. The curve marked “RHS (6.11.7)” moves down but not laterally as time increases, whereas the dashed traveling wave moves to the left. Clearly the traveling wave must “collide” with the vertically descending curve and thus must gradually alter. The consequent change propagates in from the ends. The traveling-wave solution is then, at best, a kind of intermediate asymptotic state, which, though it may be established fairly quickly, cannot endure forever.

In spite of these somewhat arcane objections of principle, propagation experiments are usually analyzed by means of the traveling-wave theory.

6.12.THE EFFECT OF HEAT TRANSFER TO THE POTTING ON THE PROPAGATION VELOCITY

The assumption that a potted conductor is uncooled is extreme,1 and in point of fact, some of the heat capacity of the epoxy potting may be available to cool the superconductor and thus slow the expansion of the normal zone (Dresner, 1980, “Propagation”). If we augment the special units of Section 6.8 with the additional requirement that kb = 1, the special unit of time is kbSb/LoJ2. The thermal diffusivity of the epoxy is kep /Sep ~ 10–4 m2/s (cf. Section 6.5). Thus heat penetrates a distance

122

CHAPTER6

d ~ [(kep/Sep)(kbSb/Lo J2)1/2 during the passage of the propagating front. Therefore the effective volumetric heat capacity for a potted wire of diameter D is

(6.12.1)

The reciprocal of the bracketed term is the correction to the propagation velocity. If we evaluate this bracket for the example conductor described in Section 6.4 using the epoxy properties given in Section 6.5, we find the bracket equals 1.40, so that the propagation velocity should be reduced by a factor of 0.713.

6.13. THE ADIABATIC HOT-SPOT FORMULA

In potted magnets wound with low-temperature superconductors (typically NbTi) the propagation velocity is often large enough (1–10 m/s) to drive the whole magnet normal before very much of the energy stored in the magnet can be converted to Joule heat. When this happens, the temperature rise of the quenched magnet can be calculated by equating the stored energy E to the enthalpy increase M 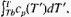where M is the mass of the magnet and cp is its average specific heat. The temperature rises are often quite modest (< 100 K) and do not injure the magnet. Such a magnet is said to be self-protecting.

Nonrecovering normal zones in potted magnets not only spread longitudinally along the conductor but also spread transversely through the epoxy potting to adjacent conductors (cf. Section 6.5). The transverse propagation velocity is less than the longitudinal propagation velocity by a factor (kt/k)1/2, where kt is the thermal conductivity in the transverse direction and k is the thermal conductivity in the longitudinal direction. While transverse propagation is much slower than longitudinal propagation (usually it is only several percent as large), it is often the most efficient means by which the normal volume of the magnet increases.

In magnets cooled with boiling helium, normal zones may arise that fail to propagate beyond a certain distance. For example, if the liquid level drops and uncovers part of the winding, that part may become normal, whereas the part still immersed may remain superconducting. Such a situation cannot be allowed to endure, for the eventual overheating of the uncovered conductor may destroy it.

How much time have we got to recognize this threat and turn off the magnet? To answer this question in detail is difficult, but a simple conservative approach is to assume the nonrecovering normal zone is uncooled either by contact with a cryogen or by longitudinal heat conduction. Then the heat balance Eq. (6.1.1)

becomes
S(dT/dt) = QP/A = rcuJ2/f = rJ2	(6.13.1)

where r = rcu /f is the effective longitudinal resistivity of the conductor. Then

Uncooled Conductors

123

(6.13.2)

Eq. (6.13.2) is called the adiabatic hot-spot formula. It has the useful characteristic that the material properties of the conductor (S, r, and T) appear on one side of the equations while the electrical property J(t) appears on the other. The right-hand side is called the adiabatic hot-spot function of the conductor. It can be calculated without too much difficulty using the formulas for the specific heat and the resistivity given in Chapter 2.

Once an upper limit to the hot-spot temperature has been decided on, the value of J2 dt is determined. The integral is composed of two parts. The first part, J2t1, is contributed by the time interval 0 < t < t1 during which the nascent normal zone is undetected. At t1, the voltage across the normal zone is large enough to be detected, and the terminals of the quenching magnet are then connected to a dump resistance, R. Thereafter, the current in the magnet falls exponentially with time with a relaxation time t2= L/R,where L is the inductance of the magnet. The integral

on the left-hand side of Eq. (6.13.2), with upper limit , then equals J	2	(t1	+ t2/2),
8

where J now represents the value of the current density when the quench began. The use of a dump resistance to dissipate most of the stored energy of the magnet outside of the dewar is an example of active protection.

The voltage V across the normal zone can be determined by a method devised by Iwasa and Sinclair (1980). For a traveling wave T(z + vt), Eq. (6.1.1) becomes

vS(dT/dz) = d/dz[k(dT/dz)]		+ (rcuJ2/f)g(T)	(6.13.3)
If we integrate Eq. (6.13.3) from z = –	to z	= 0, the symmetry	center of the
8

expanding normal zone, we find

(6.13.4)

where Tmax is the maximum temperature at the center. The integral in the middle term is the voltage difference across half the normal zone.

Aprocedure for determining the hot-spot temperature could be this: (1) Choose a voltage V that can be detected reliably. (2) Calculate Tmax from Eq. (6.13.4), using Eq. (6.8.7), say, to determine v. (3) Use Tmax to calculate t1 from Eq. (6.13.2). (4) Choose a value of R, the dump resistance, and calculate t2. The value of R is usually constrained by the maximum voltage IR across the magnet, which must not exceed the breakdown strength of the insulation. (5) Calculate the hot-spot temperature from the adiabatic hot-spot function, which is equated to J2(t1 + t2/2).

124

CHAPTER 6

When the high-temperature superconductors are used, the propagation velocity is much lower than when the low-temperature superconductors are used. The reason for this is the strong increase in the volumetric heat capacity S with temperature. For silver, the volumetric heat capacity at 77 K is three orders of magnitude as great as that at 4.2 K. The propagation velocity is then correspondingly smaller, perhaps only 1–10 mm/s. Some workers have felt that such slow propagation would worsen the problem of quench protection. In the words of Oberly et al. (1992), “The propagation velocity of the quench is of the order of 100 times slower at 20 K than at 4.2 K due to greatly increased heat capacity and greatly decreased thermal conductivity. This very slow propagation velocity can result in damage to the superconducting coil as the large stored energy is absorbed in a small region of the coil.”

Certainly magnets wound with high-temperature superconductors and operated at high temperatures cannot be self-protecting. But the problem of active protection is not worsened as one might infer from the quotation. For although the velocity v is greatly reduced (in rough inverse proportion to S), the countervailing increase in the integrand on the left-hand side of Eq. (6.13.4) largely offsets the effect of this decrease in v, and the voltage V remains detectable at quite modest temperature rises (~100 K) (Dresner, 1993, “Stability”; 1994, “On the connection”).

The question of active protection of magnets wound with high-temperature superconductors has been discussed here as though it were conceivable that such magnets occasionally quenched. The great increase in stability noted in Section 6.6 may change our view of the protection problem, but it is still too early to tell what the situation will be when we have high-temperature superconductors good enough to wind large, high-field, high-temperature magnets.

6.14. THERMAL STRESSES DURING A QUENCH

The thermal stresses that arise during a quench are generally the most influential factor in determining the maximum allowable temperature rise at the hot spot. In magnets wound with NbTi, this temperature rise can be quite large because NbTi is very strain tolerant. Even strains of several percent do not significantly degrade its critical current density. This is not so for Nb3Sn, which can stand at most oneor two-tenths of a percent strain before there is a noticeable degradation in the critical current. This is because of the frangibility of Nb3Sn, a quality that is shared by the ceramic oxide high-temperature superconductors.

Ochiai et al. (1991) have suggested the following mechanism by which thermal strain may damage silver-clad ceramic oxide superconductors. When the conductor is cooled down after reaction, the silver contracts more than the ceramic oxide, putting the silver in tension and the ceramic in compression. The silver, which is strongly annealed by the high-temperature of reaction and therefore very soft, reaches its elastic limit in the early stages of cooldown, after which its tensile stress

Uncooled Conductors

125

Figure 6.13. An idealized stress-strain curve for silver. (Redrawn from an original appearing in Dresner (1993, “Stability”) with permission of Butterworth-Heinemann, Oxford, England.)

remains fixed at its yield stress sy during the rest of the cooldown. Fig. 6.13 shows an idealized stress-strain curve for silver that will be used for the remainder of this discussion. Once the stress in the silver has saturated at the yield stress, the conductor perseveres in a state in which the silver suffers a tensile stress sy and the high-temperature ceramic oxide a compressive stress –f1 sy /f 2, where f1, is the volume fraction of silver and f2 the volume fraction of the ceramic oxide.

If a normal zone forms, the silver expands thermally more than the ceramic oxide; with enough heating, the ceramic oxide can go into tension and the silver into compression. However, the maximum compressive stress that the silver can support is – sy , so that the ceramic oxide suffers at most a tensile stress f1sy/f 2. In the case studied by Ochiai et al., the yield stress of the annealed silver was 13 MPa, whereas the ultimate tensile strength of their ceramic oxide (BSCCO) was about 60 MPa. Their tapes were 70 vol.-% silver and 30 vol.-% BSCCO, so that their f1sy /f 2 was 30.3 MPa. The thermal stresses accompanying a quench of their conductor should not harm it.

Handling, winding, and previous quenches can all work harden the silver. If more than one quench is anticipated, we may limit the hot-spot temperature so that the compressive stress in the silver never reaches sy and the silver never leaves the elastic range. Then successive quenches do not work-harden it.

Figure 6.14 depicts schematically the state of stress in a Ag/BSCCO conductor after cooldown. To simplify our analysis, let us determine strain based on material displacements from this configuration; the stress-strain curve for the silver is then that shown in Fig. 6.15. We take the stress-strain curve of the BSCCO to be entirely elastic:

126

CHAPTER 6

Figure 6.14. The state of stress in a Ag/BSSCO conductorafter cooldown. (Redrawn from an original appearing in Dresner (1993, “Stability”) with permission of Butterworth-Heinemann, Oxford, England.)

s2= E2h2– f1sy /f 2

(6.14.1)

where henceforth s represents stress, h strain, E elastic modulus, subscript 1 Ag, and subscript 2 BSCCO. The force-free condition for the conductor is

f1s1 +f2s2=0

(6.14.2)

Figure 6.15. The stress-strain curve of silver when strain is reckoned on the basis of displacements from the configuration of Fig. 6.14. (Redrawn from an original appearing in Dresner (1993, “Stability”) with permission of Butterworth-Heinemann, Oxford, England.)

Uncooled Conductors	127
while the condition that the silver and the BSCCO have the same length is
h1 + a1DT =h2+a2DT	(6.14.3)

where a1,2 are the linear coefficients of thermal expansion of silver and BSCCO, respectively, and DT is the temperature rise.

On eliminating s2 and h2 from Eq. (6.14.3), using Eqs. (6.14.1) and (6.14.2) yields

h1+ (f1/f2E2)(s1 – sy )+ (a1 –a2)DT=0

(6.14.4)

The values of h1 and s1 are determined by the intersection of the stress-strain curve of Fig. 6.15 with the straight line represented by Eq. (6.14.4.).

If this intersection is the point (–2sy /E1, – sy ), i.e., if this pointlies on the line (6.14.4), the temperature rise DT is then the largest possible that just avoids further

cold working of the silver. Ochiai et al. (1991) give the following values for the parameters: E1 = 80 GPa, E2 = 54 GPa, a1 = 2 x 10–5 K–1, a2 = 8 x 10–6 K–1. With

these values, DT = 121 K. If the intersection point is (–sy /E1, 0), the BSCCO will never go into tension at all. Then DT will be half as large as formerly, namely, 60 K. In at least one example worked in Dresner (1994, “On the connection”), at the instant the temperature rise in a normal zone in a Ag/BSCCO tape reached 100 K, the normal zone voltage was about 64 mV, which, though small, is detectable. Furthermore, this voltage was based on estimation of the propagation velocity using Eq. (6.8.7), which neglects the helpful effects of current sharing.

Notes to Chapter 6

1Nonetheless, propagation in completely insulated conductors has been examined and with some interesting results. While studying the propagation of normal fronts in a vacuum-insulated composite conductor, Bartlett, Carlson, and Overton (1979) observed that the velocity of propagation was somewhat larger (~10%) when the electrons flowed in the direction of propagation than when they flowed in the opposite direction. Gurevich and Mints (1981) suggested that the Thomson effect was responsible.Their idea was that heat would be released when the electrons flowed down a temperature gradient, speeding up propagation, whereas heat would be taken up when the electrons flowed up the gradient, slowing down propagation. They were on the right track, but the thermoelectric effect on which they focused their attention gave an effect about an order of magnitude smaller than observed, and, as Clem and Bartlett showed (1983), in the wrong direction. Clem and Bartlett explained the observed asymmetry using the Peltier effect—the heat absorbedor rejected when current passes from one material to another (copper to superconductor). This small effect is not likely to have any practical influence on magnet design, but the elegance and ingenuity of the explanation must certainly command our attention.

This page intentionally left blank.

7

Internally Cooled Superconductors

7.1. STABILITY MARGINS AND INDUCED FLOW

As mentioned in Section 1.7, magnets have been built that are cooled with supercritical helium (Tb ~ 4 K, pressure ~ 1MPa; point P3 in Fig. 1.7). Since the helium pressure is greater than atmospheric pressure, the helium must be tightly confined, and the simplest way to confine it is in the interior of a hollow conductor. Three of the magnets of IEA Large Coil Task (Beard et al., 1988) were wound with such internally cooled superconductors. Fig. 7.1 shows sketches of their conductors. The Westinghouse conductor is a cable-in-conduit conductor, a type that has already been described briefly at the end of Section 1.7. The Swiss conductor is a solder-filled cable penetrated by a central, helium-filled tube. The Euratom conductor is a coarse, flat cable in a stainless steel box.

The rationales of stability of the three magnets are quite different from one another. The Euratom and Swiss magnets were designed with “the intention to reduce the possible heat release as much as possible by using a rigid conductor and a monolithic winding pack” (Young et al., 1982). The Westinghouse design, on the other hand, foresaw the possibility of strand motion but sought to compensate for it through “a very high cooled surface [that] can be obtained by subdividing the conductor in[to] many individual strands [and that] provides the ability to rapidly remove heat input by sudden energy release and/or Joule heating from the conductor” (Young et al., 1982).1

Internally cooled conductors are not cryostable because the helium inventory available for recovery is limited. The issue of quench or recovery is decided in tens of milliseconds, whereas the residence time of the helium in the conductor is minutes or even tens of minutes. Consequently, the replacement of warm helium by fresh cold helium (that could take place in a large bath) may not occur fast enough to promote recovery. Therefore, if a thermal perturbation is strong enough, it may raise the helium temperature beyond the current sharing threshold. The Joule

129