
- •Интегральное исчисление
- •Неопределенный интеграл
- •Свойства неопределенного интеграла
- •Основные методы интегрирования
- •Интегрирование рациональных дробей
- •Интегрирование тригонометрических функций
- •Интегрирование некоторых иррациональных функций
- •Определенный интеграл
- •Свойства определенного интеграла
- •2.2 Интегрирование методом замены переменной и по частям в определенном интеграле
- •Несобственные интегралы с бесконечными пределами
- •Геометрические и физические приложения определенного интеграла
- •Контрольные вопросы и задания
Свойства неопределенного интеграла
 .
.
Проверка результата интегрирования производится дифференцированием.
 или
или
 .
. .
. .
.
Если
 ,
то
,
то ,
где
,
где – дифференцируемая функция.
– дифференцируемая функция.
Например,
 .
.
В частности, если
![]() – линейная функция, то
– линейная функция, то![]()
![]() (**),
(**),
т.к.
![]() .
Заметим, что преобразование дифференциала
.
Заметим, что преобразование дифференциала![]() к виду
к виду![]() соответствует внесению константы
соответствует внесению константы![]() под знак дифференциала (см. 1.3 п. 3).
под знак дифференциала (см. 1.3 п. 3).
Таблица основных неопределенных интегралов
 .
В частности,
.
В частности,
 .
. .
. .
В частности,
.
В частности,
 .
. .
. .
. .
. .
. .
В частности,
.
В частности,
 .
. .
В частности,
.
В частности,
 .
.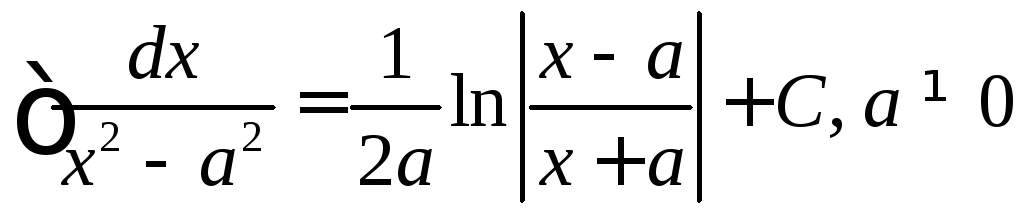 .
. .
.
Основные методы интегрирования
Непосредственное интегрирование.
Метод состоит в нахождении интеграла по таблице с помощью тождественных преобразований подынтегральной функции (выражения) с применением свойств интеграла.
Примеры:
 .
.
![]() .
.
 .
.
 .
.
В некоторых случаях сведение интеграла к табличным интегралам требует искусственных преобразований:
 .
.
 .
.
Заметим, что
последний пример можно решить по-другому,
применив в знаменателе формулу
тригонометрии
![]() :
:
 .
.
Метод подстановки (замены переменной).
Заключается во введении новой переменной интегрирования.
Пусть требуется найти интеграл
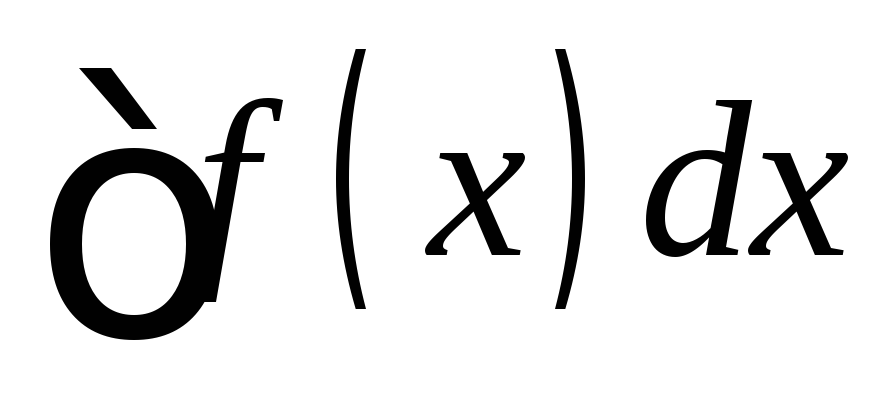 .
.
Рассмотрим
подстановку:
![]() – непрерывно дифференцируемая функция,
тогда дифференциал функции
– непрерывно дифференцируемая функция,
тогда дифференциал функции![]() и
и
![]() –(1)
–(1)
формула замены переменной в неопределенном интеграле.
После нахождения
интеграла правой части следует перейти
от новой переменной интегрирования
![]() к переменной
к переменной![]() ,
т.е. сделать обратную подстановку
,
т.е. сделать обратную подстановку![]() .
Таким образом,
.
Таким образом,
![]() ,
,
где
![]() – функция, обратная к
– функция, обратная к![]() .
.
Метод применяется, если новый интеграл проще исходного.
Пример 1. Найти
интеграл
![]() .
.
Пусть
![]()
![]() и
и
 .
.
Пример
2.
Найти интеграл
 .
.
 .
.
Пример 3. Найти
интеграл
![]() .
.
Пусть
![]() и
и
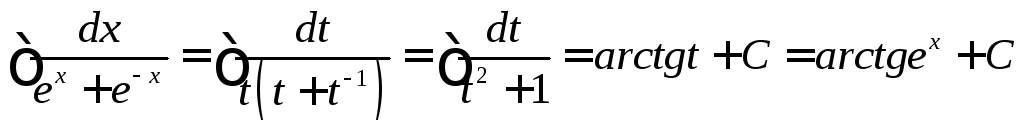 .
.
Наиболее часто на практике формулу (1) применяют в обратном порядке.
Пусть требуется найти интеграл
 ,
где
,
где – сложная функция.
– сложная функция.
Сделаем подстановку
![]() ,
тогда дифференциал функции
,
тогда дифференциал функции![]() и
и![]() .
.
Пример 4.
Найти интеграл
![]() .
.
Пусть
![]() ,
тогда
,
тогда![]() и
и
![]() .
.
Пример 5.
Найти интеграл
 .
.
 .
.
Пример 6.
Найти интеграл
 .
.
 .
.
Метод подведения (внесения) функции под знак дифференциала.
Применяется, когда
в подынтегральном выражении есть
произведение
![]() (дифференциал функции).
(дифференциал функции).
Пусть требуется
найти интеграл
![]() .
.
По определению
дифференциала функции:
![]() .
Тогда
.
Тогда![]() и, применяя свойство 5 интеграла, получим
первообразную
и, применяя свойство 5 интеграла, получим
первообразную![]() .
.
Заметим, что
рассмотренный метод равносилен
подстановке
![]() .
.
Пример 1.
![]() .
.
Данный пример
показывает самый простой случай внесения
под знак дифференциала константы, когда
![]() ,
а
,
а![]() является
дифференциалом функции
является
дифференциалом функции![]() .
Очевидно, чтобы внести функцию под знак
дифференциала, надо найти ее подходящую
первообразную.
.
Очевидно, чтобы внести функцию под знак
дифференциала, надо найти ее подходящую
первообразную.
Пример 2.
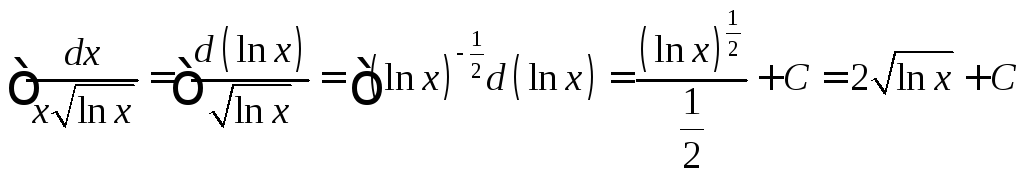 .
.
Пример 3.

![]() .
.
Приведем формулы наиболее часто встречающихся дифференциалов:
-
 ,
,
 ,
, ;
; ;
; ;
;
 ;
; ;
;
 ;
; ;
; ;
;
 ;
; .
.
Интегрирование по частям.
Метод основан на формуле интегрирования по частям:
![]() ,
(2)
,
(2)
где
![]() – непрерывно дифференцируемые функции.
– непрерывно дифференцируемые функции.
Интегрирование
по частям применяется, если интеграл
![]() правой части формулы (2) проще исходного.
правой части формулы (2) проще исходного.
Например,
в интегралах вида
![]() ,
,
где
![]() – многочлен,
– многочлен,
![]() .
.
в интегралах вида
![]() ,
,
где
![]() – многочлен,
– многочлен,![]() ,
,
![]() .
.![]()
В некоторых случаях формула применяется последовательно несколько раз.
Пример 1.
Найти интеграл
![]() .
.
Пусть
![]() ,
тогда
,
тогда![]()
![]() и
и
![]() .
.
Пример 2.
Найти интеграл .
.

 .
.
Пример 3.
Найти интеграл
![]() .
.

![]() .
.

