2.2.2. Расчет напряженности поля, созданного заряженными: бесконечно длинным цилиндром (нитью), бесконечной плоскостью, сферой, шаром

Для расчёта полей, созданных зарядами, которые равномерно распределены по сферическим, цилиндрическим или плоским поверхностям, применяют теорему Остроградского – Гаусса (раздел 2.2).

Методика расчёта полей с помощью теоремы

Остроградского - Гаусса.

1) Выбираем произвольную замкнутую поверхность, охватывающую заряженное тело.

2) Вычисляем поток вектора напряжённости сквозь эту поверхность.

3) Вычисляем суммарный заряд, охваченный этой поверхностью.

4) Подставляем в теорему Гаусса вычисленные величины и выражаем напряжённость электростатического поля.

Примеры расчёта некоторых полей

• Поле равномерно заряженного бесконечного цилиндра (нити).

Пусть бесконечный цилиндр радиусом R равномерно заряжен с линейной плотностью заряда + τ (рис. 16).

Из соображений симметрии следует, что линии напряжённости поля в любой точке будут направлены вдоль радиальных прямых, перпендикулярных оси цилиндра.

В качестве замкнутой поверхности выберем коаксиальный с данным (с общей осью симметрии) цилиндр радиусом r и высотой ℓ.

Рассчитаем поток вектора через данную поверхность:

,

где S_осн, S_бок – площади оснований и боковой поверхности.

Поток вектора напряжённости сквозь площади оснований равен нулю, поэтому

Суммарный заряд, охватываемый выбранной поверхностью:

.

Подставив всё в теорему Гаусса, с учетом того, что ε = 1, получим:

.

Напряжённость электростатического поля, созданного бесконечно длинным равномерно заряженным цилиндром или бесконечно длинной равномерно заряженной нитью в точках, расположенных вне её:

, (2.5)

где r – расстояние от оси цилиндра до заданной точки (r ≥ R);

τ - линейная плотностью заряда.

Если r < R, то рассматриваемая замкнутая поверхность зарядов внутри не содержит, поэтому в этой области Е = 0, т. е. внутри цилиндра, поля нет.

• Поле равномерно заряженной бесконечной плоскости

Пусть бесконечная плоскость заряжена с постоянной поверхностной плотностью+σ.

В качестве замкнутой поверхности выберем цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей (рис. 17). Так как линии, образующие боковую поверхность цилиндра, параллельны линиям напряжённости, то поток вектора напряжённости сквозь боковую поверхность равен нулю. Поток вектора напряженности сквозь две площади основания

.

Суммарный заряд, охватываемый выбранной поверхностью:

.

Подставив всё в теорему Гаусса, получим:

Напряженность электростатического поля бесконечной равномерно заряженной плоскости

. (2.6)

Из данной формулы вытекает, что Е не зависит от длины цилиндра, то есть напряжённость поля одинакова во всех точках. Иными словами, поле равномерно заряженной плоскости однородно.

• Поле двух бесконечных параллельных

разноимённо заряженных плоскостей

Пусть плоскости равномерно заряжены с одинаковыми по величине поверхностными плотностями +σ и –σ (рис. 18).

Согласно принципу суперпозиции,

.

Из рисунка видно, что в области между плоскостями силовые линии сонаправлены, поэтому результирующая напряжённость

. (2.7)

Вне объёма, ограниченного плоскостями, складываемые поля имеют противоположные направления, так что результирующая напряженность равна нулю.

Таким образом, поле оказывается сосредоточенным между плоскостями. Полученный результат приближённо справедлив и для плоскостей конечных размеров, если расстояние между плоскостями много меньше их площади (плоский конденсатор).

Если на плоскостях распределены заряды одного знака с одинаковой поверхностной плотностью, то поле отсутствует между пластинами, а вне пластин вычисляется по формуле (2.7).

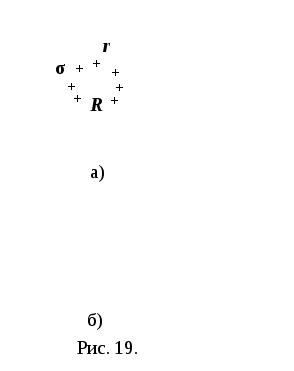
• Напряжённость поля

равномерно заряженной сферы

Поле, создаваемое сферической поверхностью радиуса R, заряженной с поверхностной плотностью заряда σ, будет центрально симметричным, поэтому линии напряжённости направлены вдоль радиусов сферы (рис. 19, а).

В качестве замкнутой поверхности выберем сферу радиуса r, имеющую общий центр с заряженной сферой.

Если r > R, то внутрь поверхности попадает весь заряд Q.

Поток вектора напряжённости сквозь поверхность сферы

Подставив это выражение в теорему Гаусса, получим:

.

Напряжённость электростатического поля вне равномерно заряженной сферы:

, (2.8)

где r – расстояние от центра сферы.

Отсюда видно, что поле тождественно с полем точечного заряда той же величины, помещённого в центр сферы.

Если r < R, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри заряженной сферы поле отсутствует (рис.19, б).

• Напряженность поля объёмно

заряженного шара

П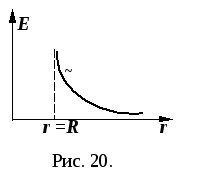усть шар радиусаR заряжен с постоянной объёмной плотностью заряда ρ.

Поле в этом случае обладает центральной симметрией. Для напряжённости поля вне шара получается тот же результат, что и в случае поверхностно заряженной сферы (2.8).

Для точек внутри шара напряжённость будет другая (рис. 20). Сферическая поверхность охватывает заряд

Поэтому, согласно теореме Гаусса

Учитывая, что , получим:

Напряжённость электростатического поля, внутри объемно заряженного шара

(r ≤ R). (2.9)

.

Задача 2.3. В поле бесконечно длинной плоскости с поверхностной плотностью заряда σ подвешен на нити маленький шарик массой m, имеющий заряд того же знака, что и плоскость. Найти заряд шарика, если нить образует с вертикалью угол α 

Решение. Вернемся к разбору решения задачи 1.4. Разница заключается в том, что в задаче 1.4 сила вычисляется по закону Кулона (1.2), а в задаче 2.3 – из определения напряженности электростатического поля (2.1). Напряженность электростатического поля бесконечной равномерно заряженной плоскости выведена с использованием теоремы Остроградского-Гаусса (2.4).

Поле плоскости однородно и не зависит от расстояния до плоскости. Из рис. 21:

.

 Обратите внимание, что для нахождения силы, действующей на заряд, помещенный в поле распределенного заряда, необходимо использовать формулу

,

а напряженность поля, созданного несколькими распределенными зарядами, находить по принципу суперпозиции. Поэтому последующие задачи посвящены нахождению напряженности электростатического поля распределенных зарядов с использованием теоремы Остроградского-Гаусса.

Задача 2.4. Опередить напряженность поля внутри и вне равномерно заряженной пластинки толщиной d, объемная плотность заряда внутри пластинки ρ. Построить график зависимости Е(х).

Решение. Начало координат поместим в средней плоскости пластинки, а ось ОХ направим перпендикулярно к ней (рис. 22, а). Применим теорему Остроградского-Гаусса для расчета напряженности электростатического поля заряженной бесконечной плоскости, тогда

.

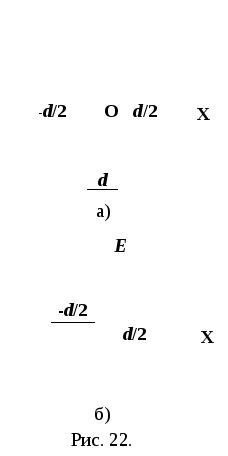Из определения объемной плотности заряда

,

тогда для напряженности получим

.

Отсюда видно, что поле внутри пластинки зависит от х. Поле вне пластинки рассчитывается аналогично:

Отсюда видно, что поле вне пластинки однородно. График зависимости напряженности Е от х на рис. 22, б.

Задача 2.5. Поле создано двумя бесконечно длинными нитями, заряженными с линейными плотностями зарядов – τ₁ и + τ₂. Нити расположены перпендикулярно друг другу (рис. 23). Найти напряженность поля в точке, находящейся на расстоянии r₁ и r₂ от нитей.

Решение. Покажем на рисунке напряжённость поля, созданного каждой нитью отдельно. Вектор направленк первой нити, так как она заряжена отрицательно. Вектор направленот второй нити, так как она заряжена положительно. Векторы ивзаимно перпендикулярны, поэтому результирующий векторбудет являться гипотенузой прямоугольного треугольника. Модули векторовиопределяются по формуле (2.5).

По принципу суперпозиции

.

По теореме Пифагора

.

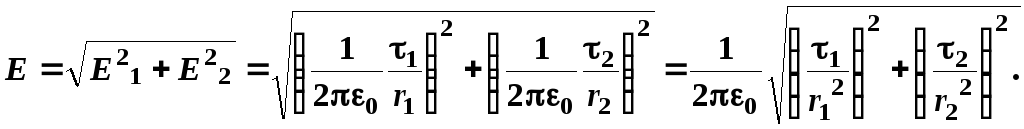Задача 2.6. Поле создано двумя заряженными бесконечно длинными полыми коаксиальными цилиндрами радиусами R₁ и R₂ > R₁. Поверхностные плотности зарядов равны –σ₁ и +σ₂. Найти напряжённость электростатического поля в следующих точках:

а) точка А расположена на расстоянии d₁< R₁;

б) точка В расположена на расстоянии R₁ < d₂ < R₂;

в) точка С расположена на расстоянии d₃ > R₁> R₂.

Расстояния отсчитываются от оси цилиндров.

Решение. Коаксиальные цилиндры – это цилиндры, имеющие общую ось симметрии. Сделаем рисунок и покажем на нем точки (рис. 24).

1. точкаА расположена внутри обоих цилиндров. Так как внутри цилиндров поля нет, то напряжённость в этой точке равна нулю:

Е_А = 0.

2. точка В расположена внутри бóльшего цилиндра, поэтому в этой точке поле создаётся только меньшим цилиндром:

.

Выразим линейную плотность заряда через поверхностную плотность заряда. Для этого воспользуемся формулами (1.4) и (1.5), из которых выразим заряд:

Приравняем правые части и получим:

,

где S₁ – площадь поверхности первого цилиндра.

С учётом того, что , окончательно получим:

3. точка С расположена снаружи обоих цилиндров, поэтому поле создаётся обоими цилиндрами. По принципу суперпозиции:

.

С учётом направлений и расчётов, полученных выше, получим:

.

Задача 2.7. Поле создано двумя заряженными бесконечно длинными параллельными плоскостями. Поверхностные плотности зарядов равны σ₁ и σ₂ > σ₁. Найти напряжённость электростатического поля в точках, находящихся между пластинами и вне пластин. Решить задачу для двух случаев:

а) пластины одноимённо заряжены;

б) пластины разноимённо заряжены.

Решение. В векторном виде напряжённость результирующего поля в любом случае записывается одинаково. Согласно принципу суперпозиции:

.

Модули векторов ивычисляются по формуле (2.6).

а) Если плоскости заряжены одноимённо, то между плоскостями напряжённости направлены в разные стороны (рис. 26, а). Модуль результирующей напряжённости

Вне плоскостей напряжённости инаправлены в одну сторону. Так как поле бесконечных заряженных плоскостей однородно, то есть не зависит от расстояния до плоскостей, то в любой точке и слева и справа от плоскостей поле будет одинаково:

.

б) Если плоскости заряжены разноимённо, то, наоборот, между плоскостями напряжённости направлены в одну сторону (рис. 26, б), а вне плоскостей – в разные.