Случайные_процессы

Часть II

Общая теория случайных процессов

1. ИСХОДНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

1.1. Случайная функция, случайный процесс и случайная последовательность

Пусть ( ,F, Р) — вероятностное пространство; (Rn,В) — измеримое пространство; t — параметр, совокупность значений которого Т в общем случае является произвольным множеством.

Определение 1.1. Случайной функцией ξ(t,ω), t T, называют измеримое отображение ξ: —> Rn пространства элементарных событий в Rn, зависящее от параметра t.

Если T = [а, b] — отрезок числовой оси, а параметр t интерпретируют как время, то вместо термина «случайная функция» используют термин «случайный процесс». При n= 1 случайный процесс ξ(t, ω), t T, называют скалярным случайным процессом, а при n≥ 2 его называют векторным случайным процессом или n-мерным случайным процессом. Векторный (n-мерный) случайный процесс ξ(t, ω), t T можно записать в виде ξ(t, ω) = (ξ1(t, ω), …, ξn(t, ω)). При этом скалярные случайные процессы ξi(t, ω) называют его координатными случайными процессами.

Если T = N, то вместо случайной функции говорят о случайной последовательности, которую обозначают также {ξk(ω)}.

При любом фиксированном значении параметра t случайная функция ξ(t, ω), t T, является случайным вектором, называемым сечением этого случайного процесса.

Если зафиксировать элементарное событие ω0 , то в этом случае ξ(t, ω0), является (неслучайной) функцией параметра t, которую называют траекторией случайного процесса, или его реализацией.

Если для случайного процесса ξ(t, ω), t T, зафиксировать произвольное значение параметра t, то получим n-мерный случайный вектор, являющийся сечением случайного процесса. Закон распределения вероятностей этого случайного вектора называют одномерным законом распределения случайного процесса ξ(t, ω), t T. Функцию распределения

x

(вероятностей) случайного вектора ξ(t, ω), t T, Fξ ( x | t ) = P(ξ (t,ω) < x) = ∫ fξ ( y | t )dy, где

−∞

1

x			y
1			1			x	x1	xn
x = .		,	y = .		,	∫ fξ ( y | t )dy =	∫... ∫ fξ ( y1 ,..., yn | t )dy1 ...dyn , называют одномерной
.			.			−∞	−∞	−∞
xn			yn

функцией распределения случайного процесса ξ(t, ω), t T, a fξ(x|t) — одномерной функцией плотности вероятностей случайного процесса ξ(t, ω), t T, которая может быть и обобщенной.

Если зафиксировать значения tk параметра t T, k = 1, …, N, то приходим к совокупности из N случайных n-мерных векторов {ξ(tk, ω)}, k = 1, …, N, с функцией распределения

x(1)	x( N )
Fξ (x(1) ,..., x( N ) | t ) = P[ξ (t( k ) ,ω) < x( k ) , k =1,..., N ] = ∫ ... ∫ fξ ( y(1) ,..., y( N ) | t )dy(1) ...dy( N ) ,
−∞	−∞

называемой конечномерной (N-мерной) функцией распределения случайного процесса ξ(t, ω), t T. В этом случае fξ(x(1), …, x(N)|t1, …, tN) — конечномерная (N-мерная) функция плотности вероятностей случайного процесса ξ(t, ω), t T (возможно обобщенная). Функ-

ции fξ(x(1), …, x(N)|t1, …, tN), Fξ(x(1), …, x(N)|t1, …, tN) задают конечномерный (N-мерный)

закон распределения случайного процесса ξ(t, ω), t T.

Не следует путать конечномерные функции плотности вероятностей (функции распределения) случайного процесса и конечномерные функции плотности вероятностей (функции распределения) его сечений. В зависимости от контекста может идти речь о N-мерной функции плотности вероятностей (функции распределения) скалярного случайного процесса и об одномерной функции плотности вероятностей (функции распределения) векторного случайного процесса.

Фактически случайный процесс ξ(t, ω), t T, можно рассматривать как совокупность всех его возможных сечений. Таким образом, в общем случае случайный процесс ξ(t, ω), t T, не может быть полностью определенным, так как он представим несчетной совокупностью своих сечений и невозможно построить совместный закон распределения всех его сечений. Поэтому любой случайный процесс ξ(t, ω), t T, Т = [а, b], в общем случае

не является полностью определенным и при решении различных задач, как теоретического, так и прикладного характера, исследователь вынужден ограничиваться использованием конечномерных законов распределений.

Определение 1.2. Случайные процессы ξ(t, ω), t T, и η(t, ω), t T, определенные на одном и том же множестве Т, в одном и том же вероятностном пространстве ( ,F, Р) и принимающие значения в одном и том же измеримом пространстве (Rn,В), называют стохас-

тически эквивалентными, если Р [ξ(t, ω) ≠ η(t, ω)] = 0 для любого t T.

Таким образом, стохастически эквивалентные случайные процессы ξ(t, ω), t T, и η(t, ω),

2

t T, могут отличаться друг от друга лишь на подмножестве 0 множества , имеющем нулевую вероятность.

Если случайные процессы ξ(t, ω), t T, и η(t, ω), t T, являются стохастически эквивалентными, то их конечномерные функции распределения совпадают, т.е.

Fξ(x(1), …, x(N)|t1, …, tN) = Fη(x(1), …, x(N)|t1, …, tN)

для любого N ≥ 1 и для любых tk Т, к = 1, …, N.

Реализации стохастически эквивалентных случайных процессов могут быть совершенно различными.

Пример. Пусть Т = [0,1] и случайная величина τ(ω) распределена равномерно на множестве Т. Рассмотрим два случайных процесса:

1,	t = τ (ω)
ξ(t, ω) ≡ 0, t T, и η(t,ω) =	, t T .
0,	t ≠ τ (ω)

Эти скалярные случайные процессы являются стохастически эквивалентными. Действительно, при любом t T имеем

Р [ξ(t, ω) ≠ η(t, ω)] = P[t = τ(ω)] = 0, так как в случае непрерывной скалярной случайной величины вероятность попадания в точку равна нулю. Любая реализация случайного процесса ξ(t, ω), t T, — тождественный нуль, а реализация случайного процесса и η(t, ω), tT имеет разрыв в случайной точке t = τ(ω).

При решении различных задач теоретического и прикладного характера в ряде случаев бывает удобной замена исходного случайного процесса стохастически эквивалентным. Тогда получаемые выводы с точностью до случайных событий, обладающих нулевой вероятностью реализации, могут быть отнесены к исходной задаче.

1.2. Математическое ожидание и ковариационная функция случайного про- цесса

Совокупность всех конечномерных законов распределения случайного процесса является полной его характеристикой. Но при решении многих прикладных задач по разным причинам ограничиваются использованием одно- и двумерных законов распределений случайных процессов и связанных с ними моментов первого и второго порядков, существование которых предполагается. Отметим, что моментами k-го порядка случайного процесса называют соответствующие моменты его сечений.

Определение 1.3. Математическим ожиданием векторного случайного процесса ξ(t, ω), t T, называют неслучайную вектор-функцию mξ(t), значение которой при каждом фиксированном t T равно математическому ожиданию случайного вектора ξ(t, ω), являющегося сечением исходного случайного процесса, соответствующего рассматриваемому значению t.

3

Если fξ(x|t) — одномерная функция плотности вероятностей n-мерного случайного процесса ξ(t, ω), t T, т.е.плотность распределения его сечения, соответствующего рассматриваемому значению t T, то, согласно определению математического ожидания случайной величины, имеем

mξ(t) = M[ξ(t, ω)] = ∫ xfξ (x | t )dx,

R n

где fξ(x|t) = fξ(x(1), …, x(n)|t), dx=dx1dx2… dxn,

	ξ (t,
	1
ξ (t,ω) =	.
.
	ξn (t,

	ω)			m (t)
				1
		, m	(t) =	.
				.
		ξ
	ω)			mn (t)

			x
			1
		, x =	.		,
			.
			xn

и для любого фиксированного k = 1, …, n имеем

n

∫ fξ (x1 ,…, xn | t) ∏ dxm ≡ fξ (xk | t), где fξ(xk|t) — плотность распределения k-й компо-

R	n−1	m=1,m≠k

ненты сечения исходного случайного процесса в момент времени t. Таким образом

		∞
mk (t) = ∫ xk				∫ fξ (x1 ,…, xn | t)		= M [ξ k (t,ω)]
		fξ (x | t )dx = ∫ xk			∏dxm dxk
R	n	−∞		n −1
			R		m=1,m≠ k

	ξ (t,ω)			M ξ (t,ω)
	1			1	.
и окончательно M [ξ (t,ω)] = M	.		=				, t T .
	.				.
	ξn (t,ω)		M ξn		(t,ω)

Математическое ожидание mξ(t) случайного процесса ξ(t, ω), t T, можно интерпретировать как его усредненную траекторию.

Определение 1.4. Ковариационной матрицей (матрицей ковариаций) n-мерного слу-

чайного процесса ξ(t, ω), t T, называют неслучайную матричную функцию Sξ(t) размерности n x n, которая при каждом фиксированном t Т представляет собой ковариационную матрицу случайного вектора ξ(t, ω), являющегося сечением исходного случайного процесса, соответствующего рассматриваемому значению t.

Если fξ(x|t) — одномерная функция плотности вероятностей n-мерного случайного процесса ξ(t, ω), t T, то

Sξ(t) = M[(ξ(t,ω) - mξ(t))(ξ(t,ω) - mξ(t))T] = ∫(x − mξ (t ))(x − mξ (t ))T fξ (x | t )dx,

R n

4

	ξ (t,
	1
где ξ (t,ω) =	.
.
	ξn (t,

	ω)			m (t)
				1
		, m	(t) =	.
				.
		ξ
	ω)			mn (t)

			x
			1
		, x =	.		,
			.
			xn

и поэтому ковариационная матрица n-мерного случайного процесса ξ(t, ω) является симметрической. Ее диагональные элементы имеют вид

Skk(t) = M[(ξk(t,ω) - mk(t))2] = D[ξk(t,ω)] = σ2ξk(t) = σ2k(t).

Таким образом, при каждом фиксированном t Т значение Skk(t) равно дисперсии скалярной случайной величины, являющейся k-й компонентой сечения исходного случайного процесса, соответствующего рассматриваемому значению t. При i ≠ j получаем, что

Sij(t) = M[(ξi(t, ω) – mi(t)) (ξj(t, ω) – mj(t))] = cov[ξi(t, ω),ξj(t, ω)], т.е. при каждом фиксиро-

ванном t Т значение Sij(t) равно ковариации двух скалярных случайных величин, являющихся i-й и j-й компонентами сечения исходного случайного процесса, соответствующего рассматриваемому значению t.

При решении прикладных задач используют понятие дисперсии σ2ξ(t) n-мерного случайного процесса ξ(t, ω). По определению полагают, что она равна следу Sp[Sξ(t)] ковариационной матрицы этого векторного случайного процесса. При этом очевидно, что σ2ξ(t) = M[(ξ(t, ω) - mξ(t))T(ξ(t, ω) - mξ(t))].

Определение 1.5. Ковариационной функцией n-мерного случайного процесса ξ(t, ω), t T, называют матричную функцию Kξ(t,s) типа n х n двух скалярных переменных t и s,

значение которой при фиксированных t, s Т равно ковариации двух случайных векторов ξ(t, ω) и ξ(s, ω), определяемой следующим образом:

Kξ(t,s) = M[(ξ(t, ω) - mξ(t))(ξ(s, ω) - mξ(s))T] = ∫ ∫(x − mξ (t))( y − mξ (s))T fξ (x, y | t, s )dxdy, где

R n R n

fξ(x,y|t,s) – двумерная функция плотности вероятностей исходного случайного процесса. Согласно определению 1.5, на пересечении i-й строки и j-ro столбца ковариационной функции Kξ(t,s) n-мерного случайного процесса ξ находится скалярная функция

Kξiξj(t,s) = M[(ξi(t, ω) – mi(t))(ξj(s, ω) – mj(s))] двух скалярных переменных t и s. Ее значе-

ние при фиксированных t и s равно ковариации двух скалярных случайных величин ξi(t, ω) и ξj(s, ω), обладающих математическими ожиданиями mi(t), mj(s), и являющихся i-й и j-й компонентами n-мерных случайных векторов ξ(t, ω) и ξ(s, ω) соответственно, т.е.

Kξiξj(t,s) = cov[ξi(t, ω),ξj(s, ω)].

Пример. Пусть α(ω) и β(ω) — скалярные случайные величины с числовыми характери-

стиками: М[α(ω)] = mα; М[β(ω)] = mβ, D[α(ω)] = σ2α, D[β(ω)] = σ2β, cov[α(ω), β(ω)] = k.

5

Найти математическое ожидание и ковариационную функцию скалярного случайного процесса ξ(t, ω) = α(ω) cos(φt) + β(ω) sin(φt), t T = [0, ∞), где φ R — постоянная.

Решаем на занятии.

Свойства ковариационной функции

Теорема 1.1. Пусть ξ(t, ω), t Т, — n-мерный случайный процесс, для которого существует ковариационная функция Kξ(t,s). Тогда

1)KTξ(t,s) = Kξ(s,t);

2)Kξ(t,t) = Sξ(t);

3)евклидова норма ковариационной функции, т.е. корень квадратный из суммы квадратов ее элементов, удовлетворяет неравенству Коши – Буняковского

|| Kξ (t, s) || ≤ σ 2ξ (t )σ 2ξ (s);

4)если φ(t) — неслучайная n-мерная вектор-функция скалярного аргумента t Т, A(t) — матричная неслучайная функция типа n x n, определенная на Т, и η(t, ω) = A(t)ξ(t, ω) + φ(t),

то в этом случае Kη(t,s) = A(t)Kξ(t,s)AT(s);

5)если ковариационная функция Kξ(t,s) непрерывна в точках диагонали t = s квадрата

Т х Т, то она непрерывна в любой другой точке этого квадрата;

6) для любого m ≥ 1 и для любого множества {tk}mk=1 Т точек отсчета квадратичная форма

m	m
∑∑Z T (i ) Kξ (ti , t j )Z ( j ) , Z (k ) = (z1k ,..., znk )T R n , k = 1,..., m
i =1	j =1

nm переменных zik, i = 1, …, n, к = 1,…, m, является неотрицательно определенной.

Доказываем на занятии.

Подсказки.

Первое утверждение следует непосредственно из определения ковариационной функции и свойств операции транспонирования матриц.

Второе утверждение следует непосредственно из определения 1.4 ковариационной матрицы и определения 1.5 ковариационной функции случайного процесса.

Третье утверждение следует из неравенства Шварца для математического ожидания

||M[α(ω)βT(ω)]||2 ≤ M[αT(ω)α(ω)]M[βT(ω)β(ω)],

если считать, что α(ω) = ξ(t, ω) – mξ(t)), β(ω) = ξ(s, ω) – mξ(s)).

Чтобы доказать четвертое утверждение, достаточно воспользоваться очевидными равенствами:

mη(t) = Mη(t, ω) = A(t)mξ(t) + φ(t),

η(t, ω) - mη(t) = A(t) (ξ(t, ω) - mξ(t)) и определением 1.5 ковариационной функции. Пятое утверждение не будем доказывать.

6

Для доказательства шестого утверждения теоремы 1.1 положим ξ (t,ω) = ξ (t,ω) − mξ (t )

и рассмотрим выражение

m		2		m m			m m
M ∑Z T	(i ) ξ	(ti ,ω)	== ∑∑Z T		(i ) M (ξ (ti ,ω),ξ (t j ,ω))Z( j ) = ∑∑Z T (i ) Kξ (ti , t j )Z( j ) .
j =1				i=1 j =1			i=1 j =1

А так как в левой части записано математическое ожидание неотрицательной случайной величины, то оно неотрицательно, и утверждение 6 доказано.

Замечание 1.1. По аналогии с коэффициентом корреляции двух скалярных случайных величин в теории случайных процессов используют понятие корреляционной функции

kξ ξ 2	(t, s) =	Kξ ξ 2		(t, s)
		1		.
1
		σ 2ξ		σ 2ξ 2
		1

Замечание 1.2. Если случайный процесс ξ(t, ω), t T, принимает значение в измеримом пространстве X C , то его называют комплексным случайным процессом. Для него

Kξ(t,s) = M[(ξ(t, ω) - mξ(t))*(ξ(s, ω) - mξ(s))]

где символ ”*” означает операцию комплексного сопряжения.

Свойства ковариационной функции комплексного процесса

1)Kξ(t,s) = (Kξ(s,t))*;

2)Kξ(t,s) = Kξ1ξ1(t,s) + Kξ2ξ2(t,s) + i(Kξ1ξ2(t,s) - Kξ2ξ1(t,s),

где ξ(t, ω) = ξ1(t, ω) + i ξ2(t, ω), и ξ1(t, ω), ξ2(t, ω) — скалярные случайные процессы.

Доказываем на занятии.

Пример. Пусть A(ω) = a(ω) + ib(ω) — комплексная случайная величина с нулевым математическим ожиданием, φ R — неслучайный скалярный параметр и комплексный случайный процесс ξ(t, ω), t T, имеет вид ξ(t, ω) = A(ω)eiφt. Найти математическое ожидание и ковариационную функцию.

Решаем на занятии.

Определение 1.6. Взаимной ковариационной функцией двух n-мерных случайных про-

цессов ξ(t, ω), t T и η(t, ω), t T, определенных на одном и том же множестве T R и на одном и том же вероятностном пространстве ( , F, Р), принимающих значения в одном и том же измеримом пространстве X Rn, называют неслучайную матричную функцию Kξ,η(t,s) размерности n х n двух скалярных аргументов t и s, значение которой при фиксированных t, s Т равно ковариации случайных векторов ξ(t, ω), и η(s, ω), определяемой следующим образом:

Kξ,η(t,s) = M[(ξ(t, ω) - mξ(t))(η(s, ω) - mη(s))T] = ∫ ∫(x − mξ (t ))( y − mη (s))T fξη (x, y | t, s )dxdy,

R n R n

где fξ,η(x,y|t,s) — функция плотности вероятностей 2n-мерного случайного вектора

7

(ξT(t, ω), ηT(s, ω)).

Согласно определению 1.6, на пересечении i-й строки и j-гo столбца взаимной ковариационной функции Kξ,η(t,s) находится скалярная функция

Kξiηj(t,s) = M[(ξi(t, ω) – mi(t))(ηj(s, ω) – mj(s))] = cov[ξi(t, ω), ηj(s, ω)].

Взаимная ковариационная функция обладает следующими свойствами:

1)Kξη(t,s) = KTηξ(s,t);

2)|| Kξη (t, s) || ≤ 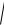σ 2ξ (t)σ 2η (s);

3)если φ1(t), φ2(t) — неслучайные n-мерные вектор-функции скалярного аргумента t Т, A1(t), A2(t) — матричные неслучайные функции типа n x n, определенные на Т R, и при k = 1, 2 ηk(t, ω) = Ak (t)ξk(t, ω) + φk (t), где ξk(t, ω) — n-мерные случайные процессы, определенные на одном и том же множестве T R, одном и том же вероятностном пространстве ( , F, Р), и принимающие значения в одном и том же измеримом пространстве X Rn, то то в этом случае Kη1, η2(t,s) = A1(t)Kξ1, ξ2(t,s)A2T(s).

Вопросы и задачи

1.1.Почему любое сечение n-мерного векторного случайного процесса является n-мерным случайным вектором?

1.2.Существует ли связь между N-мерным и (N – 1)-мерным законами распределения случайного процесса, где N ≥ 2?

Если эта связь существует, то укажите ее с использованием:

а) функций распределения; б) функций плотности вероятностей.

1.3.Возможно ли в общем случае адекватное описание случайного процесса с помощью конечномерных законов распределения?

1.4.Можно ли определить математическое ожидание случайного процесса, если известна его: а) одномерная функция распределения; б) двумерная функция плотности вероятностей?

1.5.Как связаны между собой дисперсия и ковариационная матрица случайного процесса?

1.6.В чем заключается принципиальное отличие ковариационной функции случайного процесса от его ковариационной матрицы?

1.7.Можно ли ввести корреляционную функцию для скалярного случайного процесса? В случае положительного ответа, сформулируйте ее основные свойства.

1.8.Постройте семейство реализаций (траекторий) скалярного случайного процесса ξ(t, ω) = (1 + t2)-1u(ω), где u(ω) — скалярная случайная величина, распределенная по закону Пуассона с параметром λ = 0,5.

8

1.9.Докажите, что конечномерные распределения стохастически эквивалентных случайных процессов совпадают.

1.10.Являются ли стохастически эквивалентными скалярные случайные процессы ξ(t, ω),

t Т, и η(t, ω), t Т, если T = [а,b]и:

а) η(t, ω) = ξ(t, ω)(J(t - a) - J[t - (a + b)/2]);

б) η(t, ω) = ξ(t, ω)(l-δ[t-(a + b)/2]), где J(t) — единичная функция, a δ (t) — δ-функция Дира-

ка.

1.11. Пусть а(ω) и b(ω) — неотрицательные скалярные случайные величины с известным совместным законом распределения, а скалярная случайная величина c(ω) не зависит от них и равномерно распределена на отрезке [0, 2π]. Докажите, что любое конечномерное распределение скалярного случайного процесса

ξ(t, ω) = а(ω) cos[b(ω)t + c(ω)], t Т R

не зависит от сдвига по времени, т.е. для любых N ≥ 1, tk T, k = 1, …, N, и h R, такого, что tk+h T, к = 1, …, N, имеет место тождество

Fξ(x1, …, xN|t1, …, tN) ≡ Fξ(x1, …, xN|t1+h…, tN+h).

1.12.Для случайного процесса из задачи 1.8 определите математическое ожидание и дисперсию.

1.13.Определите математическое ожидание, дисперсию и ковариационную функцию скалярного случайного процесса

ξ(t, ω) = 2u(ω)sin(νt) + 3v(ω)t2 + 5,

где ν — известный неслучайный параметр, а u(ω) и v(ω) — скалярные случайные величины с известными числовыми характеристиками: М[u(ω)] = 1; M[v(ω)] = 2; D[u(ω)] = 0,1; D[v(ω)] = 0,9; ρ(u(ω), v(ω)) = -0,3.

1.14. Пусть известны числовые характеристики двумерного случайного вектора u(ω) =

(u1(ω), u2(ω))T:
− 0,5				3	− 2
M [u(ω)] =		,	cov[u(ω)] =			.
	1			− 2	2,9

Найдите математическое ожидание, дисперсию и ковариационную функцию скалярного случайного процесса

ξ(t, ω) = u1(ω)cos t + u2(ω)sin t + t.

1.15. Найдите математическое ожидание, ковариационную функцию, дисперсию и одномерный закон распределения скалярного случайного процесса

ξ(t, ω) = α(ω)t + β(ω)t2, tk T = [0, ∞), где α(ω), β (ω) — независимые скалярные случайные величины, распределенные по нормальному закону с нулевым математическим ожиданием и дисперсией σ2 = 0,25.

9

1.16. Найдите ковариационную функцию и дисперсию скалярного случайного процесса

ξ(t, ω) = ∑[αk(ω)cos(vkt)+ βk(ω)sin(vkt)],

если vk, k = 1, …, n, — известные неслучайные параметры, αk, βk — некоррелированные скалярные случайные величины, имеющие нулевые математические ожидания и равные дисперсии D[αk] = D[βk] = σ2k.

1.17. Найдите взаимную ковариационную функцию скалярных случайных процессов ξ(t, ω) = α(ω) sin(vt) + β(ω) cos(vt)], η(t, ω) = α(ω) sin(vt) + γ(ω) cos(vt)],

если v — известный неслучайный параметр, а скалярные случайные величины α(ω), β(ω), γ(ω) являются попарно некоррелированными.

1.18. Пусть ξ(t, ω), η(t, ω) — два скалярных случайных процесса, для которых известны ковариационные функции Kξ,(t,s), Kη(t,s) и взаимная ковариационная функция Kξ,η(t,s). Найдите ковариационную функцию комплексного случайного процесса

χ(t, ω) = [a(t)ξ(t, ω)+b(t)] + i [c(t) η (t, ω)+d(t)],

если a(t), b(t), c(t), d(t) — известные неслучайные функции, определенные при t Т.

2. НЕКОТОРЫЕ ТИПЫ СЛУЧАЙНЫХ ПРОЦЕССОВ

Рассмотрим важнейшие типы случайных процессов, представляющих особый интерес для приложений.

2.1. Стационарные случайные процессы

Определение 2.1. Случайный процесс ξ(t, ω), t Т = [a, b], называют стационарным в уз- ком смысле, если для любых N≥l, tk Т, k = 1, …, N, и h R, такого, что tk + h Т, имеет место тождество

Fξ(x1, …, xN|t1, …, tN) ≡ Fξ(x1, …, xN|t1+h…, tN+h),

или, что то же самое,

fξ(x1, …, xN|t1, …, tN) ≡ fξ(x1, …, xN|t1+h…, tN+h).

Если стационарный в узком смысле случайный процесс ξ(t, ω), t Т = [a, b], имеет моменты первого и второго порядков, то его математическое ожидание M[ξ(t, ω)] ≡ mξ — постоянный вектор, а ковариационная функция зависит лишь от разности аргументов, т.е. cov[ξ(t, ω),ξ(s, ω)] ≡ Kξ(s-t).

Доказать.

Определение 2.2. Случайный процесс ξ(t, ω), t Т, называют стационарным в широком смысле, если его математическое ожидание — постоянный вектор, а ковариационная функция зависит от разности аргументов, т.е.

M[ξ(t, ω)] ≡ mξ, cov[ξ(t, ω),ξ(s, ω)] ≡ Kξ(s-t). Таким образом, из стационарности в узком смысле следует стационарность в широком смысле.

10