
- •1. Определение 2-ого и 3-его порядка. Решение систем 2х и 3х линейных уравнений с двумя и тремя неизвестными.
- •2. Алгебраические дополнения и миноры. Основные свойства определителей. Определители n-го порядка.
- •3. Различные способы вычисления определителей 3-го порядка
- •4.Правило Крамера (вывод формул…)
- •5.Матрицы. Действие над ними, обратная матрица. Ранг матрицы.
- •6. Матричная запись системы линейных уравнений. Решение с помощью обратной матрицы.
- •7.Исследование систем m линейных уравнений c n неизвестными. Метод Гаусса.
- •8. Система линейных однородны уравнений. Теорема о ненулевых решениях таких систем (доказать).
- •9.Система координат на прямой, плоскости и в пространстве. Уравнение линии на плоскости.
- •10.Простейшие задачи аналитической геометрии. Деление отрезка в данном отношении. Расстояние между точками (вывод формул).
- •11.Векторы. Направляюшие косинусы. Проекция вектора на вектор. Длина вектора. Коллинеарность, ортогональность, компланарность векторов.
- •Проекция вектора на вектор.
- •12.Линейные операции над векторами. Сложение, вычитание и умножение вектора на число.
- •13.Вывод формулы для вычисления скалярного произведения через координаты перемножаемых векторов. Свойства.
- •14.Векторное произведение. Координаты вектора векторного произведения. Его свойства. Условия колинеарности.
- •15.Приложение векторного произведения: площадь треугольника в пространстве и на плоскости через координаты его вершин.
- •16.Смешанное произведение. Вывод формулы объема параллелепипеда.
- •17. Cвойства смешенного произведения. Вывод формулы объема пирамиды и ее высоты. Условия принадлежности 4 точек к одной плоскости . Условия комплонарности 3 векторов.
- •18. Различные уравнения прямой на плоскости(наклонной,через две точки, общее, каноническое,параметрическое).
- •21.Различные уравнения плоскости (общее, уравнение плоскости проходящей через 3 точки уравнение плоскости в отрезках).
- •23. Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей. Расстояние между двумя параллельными плоскостями.
- •24. Различные уравнения прямой в пространстве. Переход от общих уравнений к каноническим и обратно.
- •25. Взаимное расположение прямой и плоскости
- •26. Угол между прямой и плоскостью. Точка пересечения между прямой и плоскостью.
- •27. Расстояние от точки до прямой в пространстве (вывод формулы). Расстояние между параллельными прямыми в пространстве.
- •28.Определение эллипса и вывод канонического уравнения.
- •29. Определение гиперболы и вывод канонического уравнения.
- •30.Определение параболы и вывод канонического уравнения.
- •31.Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
- •32.Эллипсоиды. Эллипсоид вращения. Сфера.
- •34. Параболоиды и канонические поверхности.
- •35.Цилиндрической называется поверхность,
- •36. Ко́мпле́ксные чи́сла
- •1. 2.3..
- •1. . 2.. 3..
6. Матричная запись системы линейных уравнений. Решение с помощью обратной матрицы.
В
этой статье поговорим о матричном методе
решения систем линейных алгебраических
уравнений вида 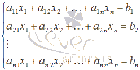 ,
которые в матричной форме записываются
как
,
которые в матричной форме записываются
как ,
где
,
где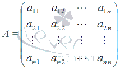 -
основная матрица системы,
-
основная матрица системы, -
матрица-столбец неизвестных переменных,
-
матрица-столбец неизвестных переменных,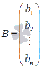 -
матрица свободных членов.
Сначала
опишем суть матричного метода, остановимся
на условии применимости этого метода,
далее подробно разберем решения
нескольких примеров.
Сразу
оговоримся, что решение систем линейных
алгебраических уравнений матричным
методом и решение СЛАУ с помощью обратной
матрицы есть одно и то же. Поэтому
рекомендуем освежить в памяти теорию
разделаобратная
матрица: определение, свойства, методы
нахождения.
Приступим.
Пусть
для матрицы А порядка n на n существует
обратная матрица
-
матрица свободных членов.
Сначала
опишем суть матричного метода, остановимся
на условии применимости этого метода,
далее подробно разберем решения
нескольких примеров.
Сразу
оговоримся, что решение систем линейных
алгебраических уравнений матричным
методом и решение СЛАУ с помощью обратной
матрицы есть одно и то же. Поэтому
рекомендуем освежить в памяти теорию
разделаобратная
матрица: определение, свойства, методы
нахождения.
Приступим.
Пусть
для матрицы А порядка n на n существует
обратная матрица  .
Умножим обе части матричного
уравнения
.
Умножим обе части матричного
уравнения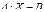 слева
на
слева
на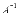 (порядки
матрицA
⋅
X и В позволяют
произвести такую операцию, смотрите
статью операции
над матрицами, свойства операций).
Имеем
(порядки
матрицA
⋅
X и В позволяют
произвести такую операцию, смотрите
статью операции
над матрицами, свойства операций).
Имеем 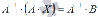 .
Так как для операции умножения матриц
подходящих порядков характерно свойство
ассоциативности, то последнее равенство
можно переписать как
.
Так как для операции умножения матриц
подходящих порядков характерно свойство
ассоциативности, то последнее равенство
можно переписать как ,
а по определению обратной матрицы
,
а по определению обратной матрицы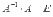 (E–
единичная матрица порядка n на n),
поэтому
(E–
единичная матрица порядка n на n),
поэтому
 Таким
образом,решение
системы линейных алгебраических
уравнений по матричному методу
определяется равенством
Таким
образом,решение
системы линейных алгебраических
уравнений по матричному методу
определяется равенством 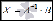 .
Другими словами, решение СЛАУ находится
с помощью обратной матрицы
.
Другими словами, решение СЛАУ находится
с помощью обратной матрицы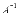 .
Мы
знаем, что квадратная
матрицаА порядка n на n имеет
обратную матрицу
.
Мы
знаем, что квадратная
матрицаА порядка n на n имеет
обратную матрицу 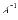 только
тогда, когда ее определитель не равен
нулю. Следовательно, СИСТЕМУn ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С nНЕИЗВЕСТНЫМИ
МОЖНО РЕШАТЬ МАТРИЧНЫМ МЕТОДОМ ТОЛЬКО
ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ ОСНОВНОЙ
МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ.
только
тогда, когда ее определитель не равен
нулю. Следовательно, СИСТЕМУn ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С nНЕИЗВЕСТНЫМИ
МОЖНО РЕШАТЬ МАТРИЧНЫМ МЕТОДОМ ТОЛЬКО
ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ ОСНОВНОЙ
МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ.
Вычислим
определитель основной матрицы и убедимся,
что он отличен от нуля. В противном
случае мы не сможем решить систему
матричным методом. Имеем  ,
следовательно, для матрицыА может
быть найдена обратная матрица
,
следовательно, для матрицыА может
быть найдена обратная матрица 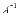 .
Таким образом, если мы отыщем обратную
матрицу, то искомое решение СЛАУ определим
как
.
Таким образом, если мы отыщем обратную
матрицу, то искомое решение СЛАУ определим
как .
Итак, задача свелась к построению
обратной матрицы
.
Итак, задача свелась к построению
обратной матрицы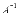 .
Найдем ее.
Мы знаем, что для
матрицы
.
Найдем ее.
Мы знаем, что для
матрицы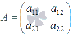 обратная
матрица может быть найдена как
обратная
матрица может быть найдена как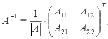 ,
где
,
где -
алгебраические дополнения элементов
-
алгебраические дополнения элементов .
.
7.Исследование систем m линейных уравнений c n неизвестными. Метод Гаусса.
Исследовать систему линейных уравнений – означает определить, какой является эта система – совместной или несовместной, и в случае её совместности выяснить, определённая эта система или неопределённая.
Условие совместности системы линейных уравнений даёт следующая теорема
Теорема 6.1 (Кронекера–Капелли).
Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу её расширенной матрицы:

Для совместной системы линейных уравнений вопрос о её определённости или неопределённости решается с применением следующих теорем.
Теорема 6.2. Если ранг основной матрицы совместной системы равен числу неизвестных, то система является определённой
Теорема 6.3. Если ранг основной матрицы совместной системы меньше числа неизвестных, то система является неопределённой.
Таким
образом, из сформулированных теорем
вытекает способ исследования систем
линейных алгебраических уравнений.
Пусть n –
количество
неизвестных, 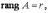
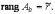 Тогда:
Тогда:
1) при  система
несовместна;
система
несовместна;
2) при 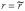 система
совместна, причём, если
система
совместна, причём, если  ,система
определённая;
если же
,система
определённая;
если же 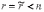 ,система
неопределённая.
,система
неопределённая.
Определение 6.1. Базисным решением неопределённой системы линейных уравнений называют такое её решение, в котором все свободные неизвестные равны нулю.
Метод Гаусса - метод последовательного исключения переменных. С помощью элементарных преобразований строк расширенной матрицы Dсистемы матрицу A системы приводят к ступенчатому виду:

 Если
среди чисел
Если
среди чисел 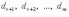 есть
отличные от нуля, система несовместна.
есть
отличные от нуля, система несовместна.
Если  то:
то:
1)
при r
= n исходная
система равносильна системе:
имеющей
единственное решение (сначала находим
из последнего уравнения  ,из
предпоследнего
,из
предпоследнего  и
т. д.);
и
т. д.);
2)
при r
< n исходная
система равносильна системе:
имеющей
бесчисленное множество решений ( -
свободные
переменные).
-
свободные
переменные).
