kvant_mech

	2n2 2π2		a	2 nπx			n2	2π2
=			∫sin			dx =				, что состоит в полном со-
	a	3			a			a	2
			0

гласии с полученными нами ранее уровнями энергии:

En =	px2(n)	=	n2 2π	2	.
	2m		2ma2

Заметим, что уравнение Шредингера Hˆψ = Eψ есть частный случай уравнения (15.2) и его решения дают состояния с определеннойэнергией.Еслиуравнение(15.2)имеетрешения, удовлетворяющие физическим требованиям к волновой функции (непрерывность, однозначность и конечность интеграла на бесконечном расстоянии) при дискретных значениях, т.е.

L= L1, L2, L3, L4,…, Ln…; Lˆψn = Lnψn , то функции дискретного спектра Ψn описывают финитные движения и могут быть

нормированы: ∫∫∫ψn 2dV =1

Для других операторов Lˆ решения, удовлетворяющие физическим требованиям, могут существовать при любых значениях L=L' из некоторого интервала L1≤L'≤ L2, тогда уравнение

(15.2) имеет вид: LˆψL′ = L′ψL′.

В этом случае говорят, Lˆ (или величина L) имеет сплошной

спектр. Функции сплошного спектраψL′ соответствуют инфинитному движению и не могут быть нормированы на единицу. Наконец, спектр оператора может быть частично дискретным и частично сплошным.

81

§29 Ортонормированность и полнота системы собственных функций

Собственные функции дискретного спектра обладают свойством ортогональности, заключающимся в том, что

∫∫∫ψm*ψndV = 0	при т≠n.
Действительно,	ˆ	и
	используем равенства Lψn = Lnψn

(Lˆψm )* = Lmψm* . Умножим первое на ψm* , а второе на ψn . Вычитая одно из другого и интегрируя, имеем:

∫∫∫[ψm* Lˆψn −ψn (Lˆψm )* ]dV = (Ln − Lm )∫∫∫ψm*ψndV .

Слева нуль, т.к. Lˆ оператор эрмитов; (Ln–Lm)≠0, и, следователь-

но, ∫∫∫ψm*ψndV = 0.

Во многих случаях уравнение (15.2) имеет кратные корни, существует так называемое «вырождение», и одному и тому же Ln соответствуют несколько (gn) разных состояний и собственных функций с «двойными номерами»: Ψn1, Ψn2, Ψn3,…, Ψn,gn. В этом случае можно составить gn разных, функций Ψnk’, являющихся линейными комбинациями функций Ψn. Возьмем первую функцию этого ряда совпадающей с Ψ1 Ψ1'=Ψ1. Ψ2'

выберем в виде Ψ2'=Ψ2+а12Ψ1 и определим а12 из требований

ортогональности Ψ2' и Ψ1': ∫∫∫ψ1* (ψ2 + a12ψ1)dV = 0 или

a12 = −	∫∫∫ψ1*ψ2dV .
	∫∫∫		ψ1		2dV

82

Теперь Ψ3' определим как линейную комбинацию Ψ3, Ψ2, и

Ψ1 Ψ3'=Ψ3+а23Ψ2+а13Ψ1 и найдем коэффициенты а23 и а13 из условияортогональностиΨ3'кΨ2'иΨ1'.Такпродолжаяпроцесс

ортогонализации, придем к ортогональной системе функций: Ψ1', , Ψgп'. Таким образом, весь набор собственных функций дискретного спектра можно считать ортогональным. Поскольку они соответствуют финитному движению, эти функции могут быть нормированы, и мы можем теперь написать условие

ортонормированности:

*	1,	m = n ,
∫∫∫ψmψndV =δmn =		m ≠ n
	0,

δmn называется символом Кронекера.

§30 Принцип суперпозиции.

Разложениепособственнымфункциямоператора

Вквантовоймеханикевводитсяещеодинважныйпостулат– принцип суперпозиции (наложения). Согласно этому принципу, если функции ϕ1, ϕ2,… ϕn изображают возможные состояния, то и функция Ψ = Σсnϕn (сn – комплексные коэффициенты) также соответствует некоторому возможному состоянию. Операторы квантовой механики, как правило, обладают свойством полноты системы их собственных функций. Это свойство заключается в том, что весьма произвольную функцию Ψ(x,y,z) можно разложить в ряд по собственным функциям оператора, подобно тому, как мы разлагаем в ряд Фурье.

Рассмотрим для простоты оператор, имеющий дискретный спектр Lˆϕn = Lnϕn . Разложение Ψ по его функциям имеет

83

вид: ψ = ∑cmϕm (x). Покажем, как можно найти сn. Умно-

m

жимрядна ϕn* (x) и,интегрируяполученноеравенство,имеем:

∫	m	∫	m
	ϕn*ψdx = ∑cm		ϕn*ϕmdx = ∑cmδmn =cn	, т.к. δmn ≠0 только

при m≠n. Аналогично для ψ* = ∑cm* ϕm* (x). Коэффициенты

m

разложения сn имеют важный физический смысл. Найдем среднее значение величины L в состоянии с волновой функцией Ψ :

			∫∫∫	ˆ	*	∫∫∫	* ˆ
L =				ψ*Lψ dV	n,m		ϕnLϕmdV =
					= ∑cncm
= ∑Lmcn*cm ∫∫∫ϕn*ϕm = ∑Lmcn*cmδmn =∑									cn		2 Ln ;
		n,m			n,m		n

сравнивая с определением среднего L = ∑wn Ln , убеждаем-

n

ся, что |cn|2=wn, т.е. квадраты модулей коэффициентов раз-

ложения имеют смысл вероятностей того, что в состоянии с волновой функцией Ψ величина L принимает значение Ln.

Пример:

Рассмотрим нормированную на единицу волновую функцию, обращающуюся в нуль на границах «ящика» с бесконечнымистенками:ψ(x) = (30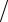a5 )1/2x(a − x).Т.к.онанесовпа-

дает с ϕn = (2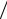a)1/2 sin(nπx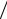a), то в этом состоянии энергия

E = px2 2m не имеет определенного значения. Разложим эту функцию по ϕn. Найдем коэффициенты разложения, имеем:

n	(		5	1/2	1/2	a		nπ x
				)	(2 a)	∫
c	= 30	a				0	x(a − x)sin	a	dx =

84

8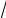15 ,åñëèесли nnнечетноен ечетн о;å;

= n3π3

0,0,åñëèесли÷åòínчетноеî å. .

Интеграл вычисляется путем двукратного интегрирования по частям:

∫a x(a − x)sin

nπx

a

∫a (a −2x)cos

nπx

dx =

dx = −

a

x(a − x)cos

nπx

{= 0}+

a

0

a

nπ

a

nπ

0

a

0

a

a

a

nπx

2

a

3

a

nπx

=

(a − 2x)

sin

{= 0}+

2a

∫sin

nπx

dx = −

2a

cos

=

2 2

3 3

0

nπ

nπ

a

n π

0

a

n π

0

a

3

2a3

4a

,åñëèесли nníнечетноеечетн о е;

= −

(cosnπ

−1)=

n3π3

3

3

n π

0,0,åñëèесли÷åòínnчетноеîå. .

Вычислим теперь среднее значение энергии в этом состоянии. Напомним: спектр энергии для частицы в ящике с беско-

нечными стенками имеет вид: E

= n2

2π2

и среднее значе-

n

2ma2

2

2

ние энергии

= ∑ En

cn

2

=

∑ n2

π

960

=

E

2

6 6

n=1,3,5..

n=1,3,5..

2ma

n π

2

1

{= π

4

5

2

= 4804 2

∑

}

=

(2k −1)

4

ma

2

π ma

k=1

96

Если не интересоваться распределением по уровням, сред-

нее значение энергии можно получить значительно проще:

a

pˆ

2

2

a

d

2

= ∫ψ*

ψdx− =

30

∫x(a − x)

[x(a − x)]dx =

E

5

dx

2

0

2m

2ma

0

30 2

a

30 2 a

ax2

x3

30 2

a3

5 2

=

ma

5

∫x(a

− x)dx =

5

−

=

5

=

.

ma

2

3

ma

ma

2

0

0

6

85

ЛЕКЦИЯ 12

§31 Представлениясостояний.Матричныеэлементы.

Матрицаоператорвсобственномпредставлении. Переходотодногопредставлениякдругому

Совокупность коэффициентов cn, с точки зрения описания состояния, напоминает по своим свойствам волновую функцию ψ(r ). Во-первых, знание совокупности cn позволяет найти ψ(r ) по формуле:

ψ(r ) = ∑cnϕn (r ). (А)

И, наоборот, известная ψ(r ) позволяет найти все cn по фор-

муле:
∫∫∫ϕn*ψdV = cn .	(В)
Во-вторых, физический смысл коэффициентов cn	также анало-

гичен физическому смыслу ψ(r ) т.к. они (точнее их квадраты) описывают вероятности того, что физическая величина принимает конкретное значение Ln, или что частица находится в объеме dV вблизи точки с координатами x, y, z (r ). Ввиду этого совокупность коэффициентов cn называют волновой функцией в L-представлении, а ψ(r ) волновой функцией в координатном представлении, Переход от одного представления к другому осуществляется с помощью приведенных формул (А) и (В).

Можно получить более общие формулы для перехода от

одного представления (L-) к другому (M-), где Lˆ и Mˆ два эрмитовых оператора, также найти вид любого эрмитова оператора в произвольном L-представлении. Ограничимся операторами, имеющими дискретный спектр.

Пусть имеется совокупность собственных функций опера-

86

ˆ	ˆ		ˆ
тора L :	Lϕn = Lnϕn и произвольный эрмитов оператор M ,
переводящий волновую функцию Ψ в Ψ‘:
	ˆ		16.1
	Mψ =ψ′.
Разложим Ψ и Ψ′ по ϕn: Ψ=Σcnϕn		и Ψ′=Σc’nϕn	где совокупности
cn и c’n есть волновые функции в		L-представлении. Их часто за-

писывают в виде матрицы-столбца. Подставим разложения в (16.1) ∑cn Mˆ ϕn = ∑cn′ϕn . Умножая обе части на ϕm* , интегрируя и пользуясь условием ортонормированности, получим:

cm′ = ∑Mmncn ,где Mmn = ∫∫∫ϕm* Mˆ ϕndV . n

Величины Mmn можно расположить в квадратную таблицу:

	M11		M1n
ˆ
M =	M n1		M nn	, имеющую конечное или бесконеч-

ноечислостроки столбцов, называемуюматрицей, авеличины Mmn называются матричными элементами этой матрицы. Ма-

	ˆ			ˆ
трица M , является оператором				M в L-представлении и пре-
образует волновую функцию cˆ				в другую – cˆ′. В символиче-
ской записи		ˆ
		cˆ′= M cˆ .
В	частности, в		своем	собственном	представле-
нии	ˆ	= Mnψn	матрица диагональна,		поскольку
	Mψn

Mmn = ∫∫∫ψm* MˆψndV = Mnδmn = 0 при m≠n и на главной диагонали стоят ее собственные значения.

87

§32 Коммутативность операторов и ее физический смысл

Мы уже видели на примере операторов pˆx и xˆ , что они могутнеподчинятьсякоммутационномузакону.Коммутационные свойства операторов определяют, могут ли они иметь общие собственные функции.

Пусть имеются два эрмитовых оператора Lˆ и Mˆ , соответствующие физическим величинам L и M . Докажем два утверждения:

1. Если существуют волновые функции ψL′M ′ , соответствующиесостояниям,вкоторых L и M принимаютточныезначения L = L′ и M = M ′, причем эти функции образуют полный

набор, то операторы Lˆ и Mˆ коммутируют. Доказательство: По условию имеем два равенства:

ˆ

′ = L′ψ ′

′ и

ˆ

′ ′ = M ′ψ ′ ′ .

Подействуем на

L ψ ′

M ψ

L M

L M

L M

L M

ˆ

ˆ

обе части равенств перекрестно операторами L

и M , тогда

ˆ ˆ

′ ˆ

′

′

′

,

MLψL′M ′

= L MψL′M ′

= L M

ψL′M

LMψL′M ′

= M LψL′M ′

= M LψL′M ′

. В правой части равенств

ˆ

ˆ

′ˆ

′ ′

ˆ

ˆ

ˆ ˆ

′ – операто-

стоят равные числа! Откуда LMψ

′ ′ = MLψ ′

ры коммутируют.

L M

L M

2. Пусть операторы коммутируют. Тогда существуют такие

состояния, в которых L и M принимают одновременно точ-

ные значения L′ и M ′.

ˆ

Доказательство: Пусть ψL′ собственная функция оператора

ˆ

ˆ

L , т.е. L ψ ′ = L′ψ

′ . Подействуем оператором M и исполь-

L

L

зуем коммутативность:

88

MLˆ ˆψL′ = LMˆ ˆψL′ = L′(MˆψL′),

т.е. MˆψL′ является собственной функцией оператора Lˆ , принадлежащей собственному значению L′. Если L′ не вырождено, то функция MˆψL′ может отличаться от ψL′ только постоянныммножителем M ′,т.е. MˆψL′ = M ′ψL′ иψL′ является одновременно и собственной функцией оператора Mˆ , принадлежащей собственному значению M ′. Если же L′вырождено, то можно доказать, что из собственных функций ψL′ (k= 1,2,3,…gL’) можно построить такие линейные комбинацииk , которые будут собственными функциями оператора Mˆ .

Итак, мы доказали, что для существования состояний, в которых величины L и M одновременно имели бы точные зна-

чения, необходимо и достаточно, чтобы операторы Lˆ и Mˆ коммутировали.

§33 «Точное» соотношение неопределенностей

Пусть Lˆ и Mˆ не коммутируют. Тогда в состоянии с волно-

вой функцией Ψ величины L и M (в общем случае обе) не имеют определенных значений и обладают средними квадра-

L

= ∆

L

и

M

2 = ∆

M

отлич-

тичными дисперсиями ∆ 2

ˆ

∆

ˆ

ˆ

ˆ

нымиотнуля.Введемоператоры L = L − L

, M = M − M

иэрмитов оператор Nˆ такой, что LMˆ ˆ − MLˆ ˆ = iNˆ .

Вкачестве упражнения студентам предлагается доказать,

что LMˆ ˆ − MLˆ ˆ = Lˆ Mˆ - Mˆ Lˆ = iNˆ .

Длявыводаобщегосоотношениянеопределенностейприме-

89

ним искусственный прием. Рассмотрим неотрицательный интеграл, являющийся функцией вещественного параметра α:

I (α) = ∫ (α∆Lˆ −i∆Mˆ )ψ 2dV =

=∫[(α∆Lˆ −i∆Mˆ )ψ]*[(α∆Lˆ −i∆Mˆ )ψ]dV =

=∫[(α∆Lˆ +i∆Mˆ )ψ* ](α∆Lˆ −i∆Mˆ )ψdV =

=∫ψ*[α2∆Lˆ2 −iα(∆Lˆ∆Mˆ −∆Mˆ ∆Lˆ)+∆Mˆ 2 ]ψdV

Подставляя вместо коммутатора iNˆ , окончательно находим неравенство:

I(α)= ∫[ψ* (α2 ∆Lˆ 2 +αNˆ +∆Mˆ 2 )ψdV =α2 ∆L2 +αN +∆M 2 ≥0.

Чтобы квадратный трехчлен был неотрицательным, необходимо, чтобы его дискриминант (N )2−4∆L2 ∆M 2 был неполо-

жительным, откуда ∆L ∆M ≥ N2 .

ПоследняяформулапредставляетсобойобобщенноесоотношениенеопределенностейГейзенберга.Вчастномслучае,когда

Lˆ = xˆ,а Mˆ = pˆx изсоотношениякоммутации xpˆˆx − pˆx xˆ = i , мы приходим к формуле:

∆px∆x = 2 .

§34 Оператор производной по времени.

Интегралы движения. Уравнения Эренфеста. 2-й закон Ньютона в квантовой механике.

Вернемся к формуле среднего значения L = ∫ψ*LˆψdV . Продифференцируем левую и правую части по времени:

90