olimpiady_matematika

Запишем необходимые и достаточные условия для двух по

ложительных решений
	D > 0,			p < 6,
	xв > 0,			p > 0,
	p2 + p – 6 > 0			p (– ; –3) (2; )

			p (2; 6).
Единственное положительное решение достигается при вы
полнении следующих условий:
			D = 0,				p = 6,
			xв > 0;				p > 0;		p = 6,
			p2 + p – 6 < 0;				p (–3; 2);
									p (–3; 2].
			p2 + p – 6 = 0,				p = {–3; 2},
			xв > 0				p > 0

Причем положительное решение вычисляется по формуле

x = p + –p + 6 .

Рассмотрим x > 0 и y = –1. Подставляя во второе уравнение сис темы y = –1, получим квадратное уравнение

						D	= p, x		= p –p + 2 .
x2 – 2px + p2 + p – 2 = 0, где ---- = 2 – p, x								1, 2
					4		в
Необходимые и достаточные условия для двух положитель
ных решений
				D > 0,
				xв > 0,		p (1; 2).
				p2 + p – 2 > 0
Единственное положительное решение достигается при вы
полнении следующих условий:
			D = 0,
			xв > 0;			p = 2,
			p2 + p – 2 < 0;			p (–2; 1), p (–2; 1] {2}.
			p2 + p – 2 = 0,			p = 1
			xв > 0

Объединяя решение, получим ответ.

4R2

10. ОТВЕТ: Smin = --------- ; 3 : 19.

66

163

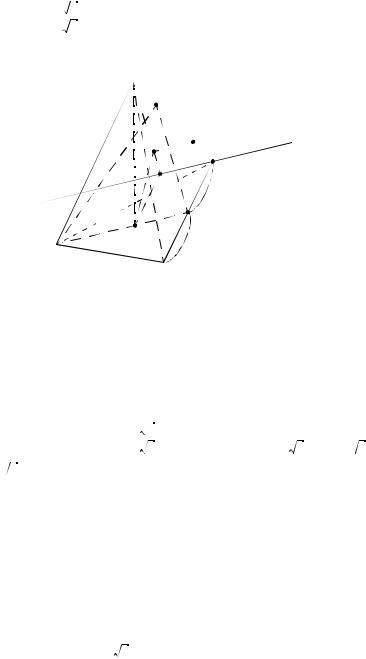
РЕШЕНИЕ. В правильной треугольной пирамиде TABC

TO1	2		= h, AT = b, AB = a, точка
(рис. 68) -----------	= ------ , где высота TO	1
AT	3
O — центр описанной сферы, AD — высота основания.
	T
	M
			M1	l

P

C

F

O

D

O1

A

B

Рис. 68

1) Из треугольника AOO1

R2 = (h – R)2 + (AO1)2.

2) Из треугольника ATO1

b2 = h2 + (AO1)2.

		h	2		4R			4R	, a =
С учетом условия -- =			------ , h = ------- , AO				1	= ----------
		b	3			3		3 2
AD = R 2 .
3) Наименьшая площадь сечения равна
S	1	AD•h		, где h		= ρ(TC, AD).
	= --		min		min
ADM	2

(1)

(2)

4R

------- ,

6

Проведем прямую l AD через точку C. Тогда две пересекаю щиеся прямые TC и l образуют плоскость α, а расстояние меж ду скрещивающимися прямыми TC и AD равно расстоянию между плоскостью α и прямой AD, т. е. ρ(O1, α) = ρ(TC, AD). TO1 (ABC ), в плоскости ABC проведем O1F l, т. е.

		a	2R
O F BC, O F = --			= ------- . По теореме о трех перпендикуля
1	1	2	6

164

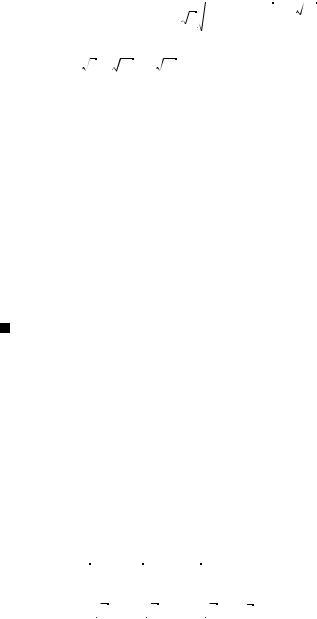
рах TF l. Из треугольника TO1F следует O1P = ρ(O1, α), где

O1P TF.

TO1•O1F

4R•2R

4R

O P = ----------------------------

= ----------------------------------------------- = --------- .

1

TF

3 6

16R2

4R2

33

------------ +

---------

9

6

4) S

1

2R

4R

4R2

min

= --

• ------- •

--------- =

--------- .

2

2

33

66

5) Из треугольника TFO

TP

TO12

=

8

1

следует --------

= -----------

-- .

PF

FO2

3

1

6) В треугольнике TFC проводим PM

TM

=

8

1

l, тогда ------------

-- .

M1C

3

M1 — положение точки при наименьшей площади сечения.

7) V

= V

1

H

S , где H

— перпендикуляр к

1

M1ADC

= --

M1

M1

3

ADC

плоскости ABC, проведенный из точки M . V

=

1

,

TABC

-- TO S

1

3

1

ABC

S

=

1

S

, H

3

V1

3

, V

= V

– V ,

V1

=

ADC

--

ABC

M1

= -----

TO , -----------------

= -----

2

TABC

-----

2

11

1

V

TABC

22

1

V

2

3

= ----- .

19

Второй тур, 2009 г. Вариант 2

1. ОТВЕТ: 10; 8.

РЕШЕНИЕ. Пусть 1 й автомобиль расходует на 100 км x л бензина, а 2 й автомобиль расходует (x – 2) л бензина. Тогда 1 й

			100		км, а 2 й
автомобиль расходует 1 л бензина на прохождение --------
			x
		100	км.
автомобиль на прохождение -------------
		x – 2
100	100	= 2,5	x2 – 2x – 80 = 0, x			= 1 9,
По условию -------------	– --------			1, 2
x – 2	x

откуда x = 10 л для 1 го автомобиля и 8 л для 2 го автомобиля.

2.			π			2
	ОТВЕТ: x =	(–1)n• --		+ πn		, n {0}	N.
			4

РЕШЕНИЕ. 2 cos2 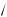x = sin x . ОДЗ: x 0. Преобразуем ис ходное уравнение

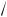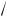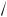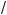2 sin2 x + sin x – 2 = 0

165

и найдем корни: sin		–1 3
		x = ------------------- .
		2	2
Если sin	1
	x = ------ , то
	2
	x = (–1)n•		π	N.
			-- + πn, n {0}
			4
Возводя уравнение в квадрат, получим ответ.
	1
3. ОТВЕТ: -- ; 4.
	8
РЕШЕНИЕ. (log2 x + logx 2 + 2)(log2 x – log2x x) = 6.
ОДЗ: x > 0, x = 1, x =		1
		-- .
		2

Переходя к основанию, равному 2, получим, что:

log		1		+ 2 log		log2 x			= 6.
	2	x + --------------			2	x – --------------------------
		log2	x			1 + log2	x

Обозначим log2 x = t, тогда уравнение принимает вид:

(t2

+ 2t + 1)

t + t2 – t

= 6 и (t + 1)t = 6, откуда

--------------------------------

• -----------------------

t

t + 1

t2 + t – 6 = 0, t

1

= –3, t

2

= 2.

Тогда

log2 x = –3,

x =

1

-- ,

log2 x = 2

8

ОТВЕТ:

8

; 1

x = 4.

4.

(1; 8).

--

9

РЕШЕНИЕ. x

1 + logx ----------------- < 0. ОДЗ:

9x – 8

Преобразуем исходное неравенство:

x

logx ----------------- ) < logx

9x – 8

x

----------------- > 0,

9x – 8

x > 0, x = 1.

1

-x- .

При решении неравенства рассмотрим два случая: x > 1 и 0 < x < 1.

166

x > 1,						x > 1,
x	<	1	;			x2 – 9x + 8
9----x-----–------8--		--				---x----(--9----x----–-------8---)---
		x
0 < x < 1,						0 < x < 1,
x	>	1				x2 – 9x + 8
9----x-----–------8--		--				---x----(--9----x----–-------8---)---
		x

x (1; 8),

8	; 1	.
x --
9

< 0;

> 0;

5. ОТВЕТ: x [0; 1) (1; 9].

	x – 5	x + 4	2	x + 1		x 0,
РЕШЕНИЕ.	-------------------	-------------	--------------------- . ОДЗ:
	1 –	x		x + 4		x = 1.

Обозначим x = t 0, тогда x = t2, и подставим в исходное неравенство:

t2 – 5t + 4	2t + 1
--------1-----–------t---------	--------------- .
	t + 1

Раскладывая левую часть неравенства на множители, полу чим:

2t + 1

( t – 4)( t – 1)

2t + 1

---------------

+ t – 4 0,

t + 4

1 – t

t + 4

t = 1

t2 + 2t – 15

,

( t + 5)

( t – 3)

----------t----

+------4---

--------

-----------------------------------

0,

t + 4

t = 1

t = 1.

Откуда с учетом, что t 0, следует:

t [0; 1) (1; 3].

Переходя к переменной x, получим:

x [0; 1) (1; 9].

6.

π

ОТВЕТ: -- .

4

РЕШЕНИЕ. y = 0,5(x2 – 6x), M(2,5; –4,5).

Запишем уравнение касательной

y = 0,5( x02 – 6x0) + (x0 – 3)(x – x0), где x0 — абсцисса точки касания.

Подставляя координаты M в уравнение, получим, что –4,5 = 0,5( x02 – 6x0) + (x0 – 3)(2,5 – x0),

167

откуда x2	– 5x	0	+ 6 = 0 и
0
					x01 = 3,
					x02 = 2.
Найдем для каждого значения x0
			k1 = y′(x01) = x01 – 3 = 0,
			k2 = y′(x02) = x02 – 3 = –1.
Это соответствует тому, что угол α1 наклона одной касатель
ной к положительному направлению оси OX равен 0; а α						=	π
							-- .
			2				4

Следовательно, угол между касательными ϕ = |α		– α	π
			| = -- .
	1	2	4
7.	243π
	ОТВЕТ: ------------ .
	52

РЕШЕНИЕ. AKB — внешний к AKC.

AKB = C + KAC, следовательно, KAC = B = α, C = β.

В AKC: AKC = 180° – α – β				AKC = A.
В ABC: A = 180° – α – β
KC	AC	AK		AC = 6; AB = 15.
AKC ABC: --------	= -------- =	--------
AC	BC	AB

			S					15 + 6 + 18							39	= 19,5.
	r = ---			, p = ------------------------------ =											-----
			p							2					2
S			=															27		39 ,
	ABC				19,5•1,5•13,5•4,5 = -----
																			4
	r =	27		39•2						27				= πr2 =					243π
		------------------------							= ------------- ; Sкр										------------ .
			4•39						2	39									52
8. ОТВЕТ: 12 ед2; A(4; 6).
РЕШЕНИЕ. S					= S						+ S					=		1	AD(OA			+ A	B ) =
		OAB							AOD			ABD						--			1
																		2				1	1
= 3AD (рис. 69).
	AD = AA										x2			x	+ 6 – A D;
						1	– A D = ---- –							--
									1		8			2					1
ODA					OBB						OA1				A1D				x	=
				1							: -----------			= -----------				--
										1	OB		1		BB		1		6

168

=

A1D

A D =

x

y

-----------

-- .

3

1

2

x2

A

AD = ----

– x + 6,

8

x2

D

B

S OAB = 3

---8- – x + 6

,

S′ =

3x

O

A1

B1

x

----- – 3 = 0, x

A

= 4,

4

тогда A (4; 6).

Рис. 69

S

= 3

16

– 4 + 6

= 12.

-----

min

8

9. ОТВЕТ: (– ; –5) (–3; 2) [7; + ) {6}, если a (– ; –5) [7; + ) {6},

x1 = 3 + 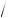a2 – 4a – 12 , x2 = 3 – a2 – 16 ,

если a (–3; 2), x1, 2 = 3 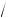a2 – 4a – 12 .

		x +	x		2
		----------------			= x	2	– 6x + 25.
РЕШЕНИЕ.		x		– a
Случай 1. Если x > 0, то
		x2 – 6x + 21 + 4a – a2 = 0.
D	= a2 – 4a – 12 = (a + 2)(a – 6), x								= 3.
----								в
4

Найдем корни уравнения:

x1, 2 = 3 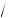a2 – 4a – 12 .

Два различных решения имеют место, если:

D > 0,	a (–3; –2) (6; 7).
xв > 0,
–a2 + 4a + 21 > 0

Единственное решение достигается при выполнении сле дующих условий:

D = 0,

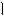xв > 0,

–a2 + 4a + 21 < 0, a (– ; –3] [7; + ) {–2; 6}. –a2 +4a + 21 = 0,

xв > 0

169

Случай 2.Если x < 0, то

x2 – 6x + 25 – a2 = 0,	D	= a2 – 16; x = 3,
	----
	4	в

Корни уравнения x1, 2 = 3 a2 – 16 . Двух решений нет. Единственное решение достигается при 25 – a2 < 0, т. е.

a (– ; –5) (5; + ), т. е. x = 3 – a2 – 16 . Объединяя решение получим ответ.

10. ОТВЕТ: 32.

РЕШЕНИЕ. a = 43 , ρ(A, α) = 3 (рис. 70).

B

M L

α(A1, M, N)

A C

B1 N

A1

C1

Рис. 70

Сечение A1MLN делит сторону BC в отношении BL : LC = 2 : 1,

Sпр

S = ------------- , S = S = S – S (рис. 71).

сеч cos ϕ пр AMLC ABC BML

B

F M

E

L

A C

Рис. 71

170

S		=	a2	3	a2	3	a2 3
	пр		------------		– ------------		= ------------ = 8 3 .
			4		12			6
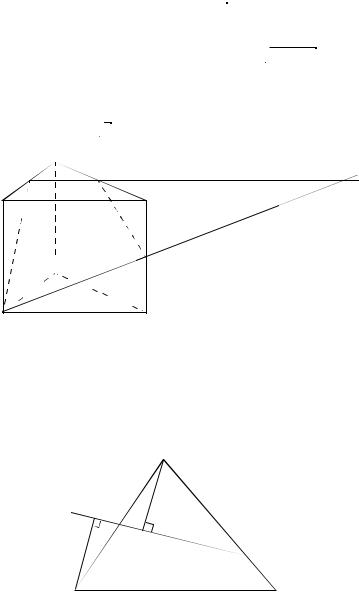
A1A (ABC ),			AF ML,				BE ML,		AF = BE.
	S				a2 3		1
		BML		= ------------		= -- •BE•ML.
					12		2
Из BML: ML2			a2		4a2		a2	a2	a	13 .
			= -----		+ --------	– -----		= ----- •13, ML = --
			4		9		3	36	6

a2	3	1	a	a	3	12
------------		= --	BE• --	13 BE = AF = ----------		= --------- .
12		2	6		13	13

AP A1F в AA1F,

AP = 3 по условию задачи.

Из APF находим sin ϕ =			AP		13	, cos ϕ =	13	3	,
			-------	= ---------			1 – -----	= ------
			AF	4			16	4
S		= 8		3	= 32.
	сеч		3 : ------
				4

Второй тур, 2009 г. Вариант 3

1. ОТВЕТ: 36; 30	км		.
	------
	ч

РЕШЕНИЕ. Обозначим скорость 2 го велосипедиста x (км/ч), тогда скорость 1 го велосипедиста (x + 6) (км/ч). Время, за кото

1

рое 1 й велосипедист пройдет 1 км, равно ------------- (ч), а время, за x + 6

1

которое 2 й велосипедист пройдет 1 км, равно -x- (ч). По условию задачи 1 й велосипедист проходит это расстояние на 20 с быст

		1	1	20	, откуда x = 30.
рее. Составим уравнение: --			– -------------	= -----------
		x	x + 6	3600
2.	π	+	πn, n Z.
	ОТВЕТ: (–1)n + 1• --
	6

РЕШЕНИЕ. Преобразуем исходное уравнение:

1 + sin x = –2 sin x, sin x 0.

171

Возводя в квадрат обе части уравнения, получим 1 + sin x = 2 sin2 x,

корнями которого являются:

1 sin x = 1 и sin x = – -2- .

Решение уравнения имеет вид:

π	+ πn, n Z.
x = (–1)n + 1• --
6

1

3. ОТВЕТ: -6- .

РЕШЕНИЕ. Запишем ОДЗ исходного уравнения:

x (0; 1)	1;	7	.
		--
		6

Перейдем к основанию, равному 2:

log2 (7 – 6x)

---------------------------------- = –1 log2 x

или

1 log2 (7 — 6x) = log2 -x- .

1

Откуда следует, что: 7 – 6x = -x- .

После преобразования получим квадратное уравнение: 6x2 – 7x + 1 = 0.

1

Корни этого уравнения x1 = 12, x2 = -6- .

1	удовлетворяет ОДЗ.
Только один корень --
6
4. ОТВЕТ: (– ; –2)	3	; 3		(3; + ).
	--
	2

РЕШЕНИЕ. Преобразуем исходное неравенство:

(x – 3)(x + 3)						2x – 3
			1			-----------------	> 0,
(---x-----–------3----)--(--x----2----+------3----x----+-------9---)-		> x-----+-------2-				x + 2
						x = 3.
Решением этого неравенства являются интервалы
3	; 3 (3; + ).
x (– ; –2) --
2
		4	.
5. ОТВЕТ: (–4; –2) –1; – --
		5

172