2.9. Частные производные и полные дифференциалы высших порядков.

Для числовой функции двух переменных частными производными высших порядков будут частные производные от частных производных первого порядка

.

Частных производных второго порядка может быть образовано четыре

.

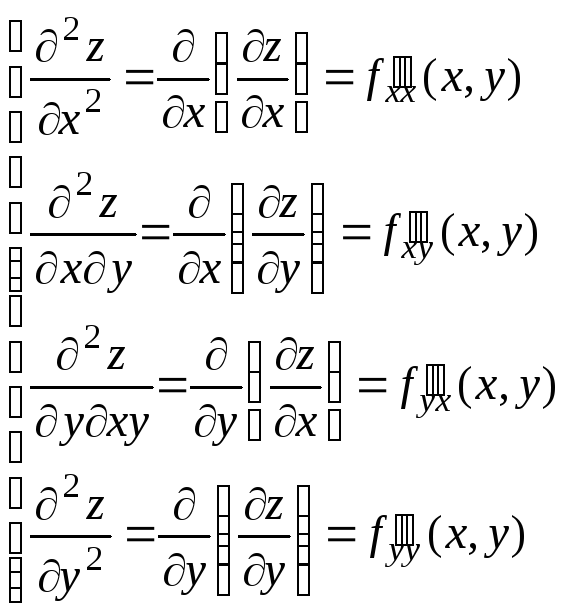Пример.

Для функции найти частные производные до второго порядка включительно.

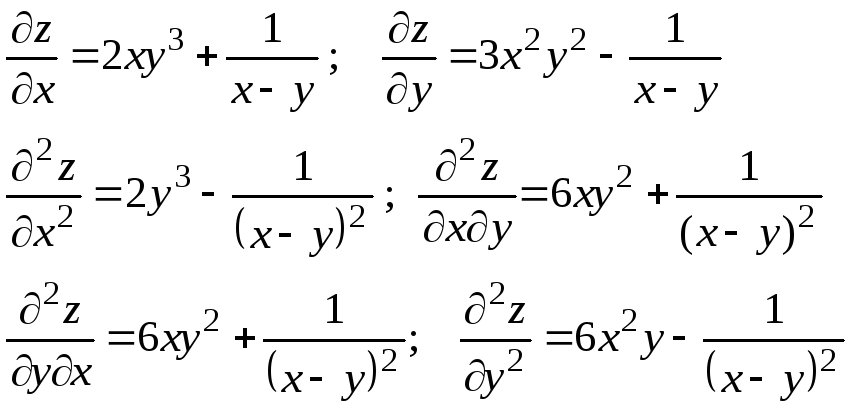
В приведенном примере оказалось, что смешанные производные совпадают

. (2.9.1)

Такое совпадение не является случайностью. Можно строго доказать, что порядок дифференцирования по различным переменным подчиняется закону коммутативности

.

Полный дифференциал функции имеет вид

.

Дифференциалом второго порядка называется дифференциал от полного дифференциала

.

Эту формулу похожую на формулу для квадрата суммы можно записать символически

. (2.9.2)

Можно показать, что дифференциал n–го порядка (дифференциал от дифференциала n–1 порядка) вычисляется по формуле

. (2.9.3)

Можно так же показать, что дифференциалы высших порядков для сложных функций не обладают свойством инвариантности формы.

2.10. Свойства функций, дифференцируемых на интервале.

Теорема 1 (Теорема Ролля). Если функция непрерывна на отрезке, дифференцируема на интервалеи принимает на концах отрезка одинаковые значения, то существует хотя бы одна точка, в которой производная функции равна нулю.

Доказательство:

Воспользуемся теоремой 2 раздела 1.17, согласно которой, если , то она принимает на отрезкенаибольшее и наименьшее значенияи.

Если , тои теорема очевидна. Еслито, по крайней мере, одно из этих значений функция принимает в некоторой точке.

Пусть, например, . Тогда приимеем

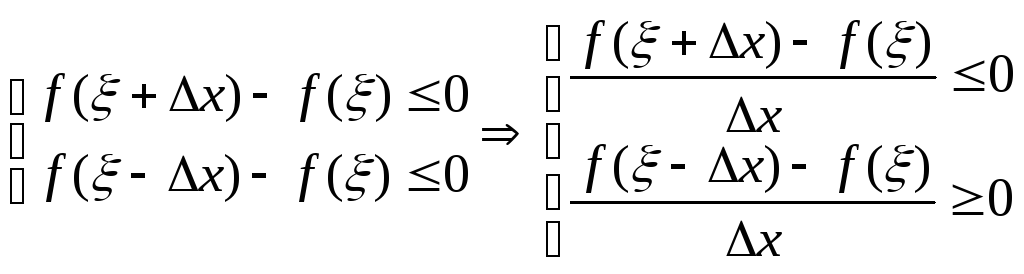
Выполняя предельный переход в этих неравенствах при , получим

.

Таким образом, – что и требовалось доказать.

Теорема 2 (Теорема Коши). Если функции инепрерывны на отрезке, дифференцируемы на интервалеидля всех, то существует хотя бы одна такая точка, в которой выполняется соотношение

. (2.10.1)

Доказательство:

Введем вспомогательную функцию

.

Подберем число , чтобы выполнялось условие теоремы Ролля

.

.

К функции

,

применим теорему Ролля

.

Таким образом

,

что и требовалось доказать.

Теорема 3 (Теорема Лагранжа). Если функция непрерывна на отрезкеи дифференцируема на интервале, то существует хотя бы одна такая точка, в которой выполняется соотношение

. (2.10.2)

Формула (2.10.2) называется формулой Лагранжа для конечных приращений.

Доказательство этой теоремы следует из теоремы Коши как частный случай при .

Г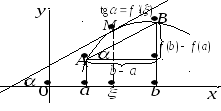еометрический смысл формулы Лагранжа

Заключается в том, что на дуге АВ существует точка М, касательная в которой параллельна хорде AB.

2.11. Раскрытие неопределенностей по правилу Лопиталя

Теорема (Теорема Лопиталя). Если функции иудовлетворяют на отрезкеусловиям теоремы Коши, обращаются в нуль в некоторой точке

,

и существует предел отношения производных , то существует и предел самих функцийи эти пределы равны между собой

. (2.11.1)

Доказательство:

Внутри отрезка выберем произвольную точку. Для вновь образованного отрезказапишем формулу Коши

.

Учитывая, что , находим

.

Переходя к пределу при получаем

. (2.11.2)

Что и требовалось доказать.

Формулы (2.11.1) и (2.11.2) называют правилом Лопиталя для раскрытия неопределенностей вида .

Замечание:

Следует отметить, что по теореме Коши (2.11.2) точка выбирается специальным образом и стремится к нулю не как угодно, а специально подобранным способом. Предел же в (2.11.1) записан самый обычный – так его проще вычислять. Поэтому если обычный предел правой части равенства (2.11.1) не существует, то это еще не означает, что не существует предел правой части равенства (2.11.2).

На практике правило Лопиталя удобно использовать для раскрытия неопределенностей вида , когда числитель или знаменатель при дифференцировании упрощаются.

Примеры.

1. .

2. .

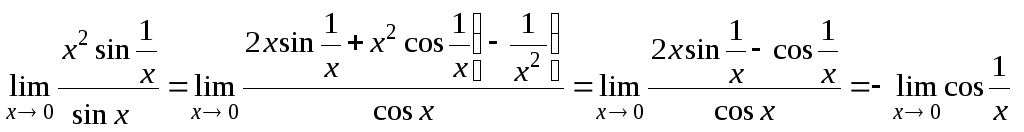Последний предел не существует из-за колебаний . Однако это не означает, что не существует и предел левой части:

.

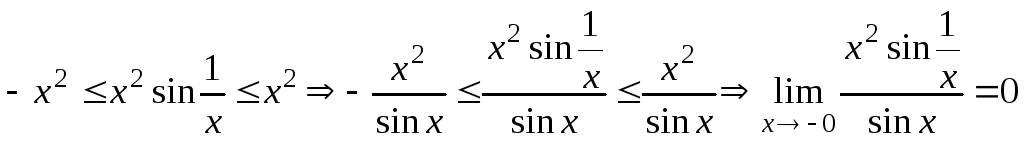Это как раз случай описанный в замечании к теореме Лопиталя.

3.

Правило Лопиталя остается справедливым и при . В самом деле

.

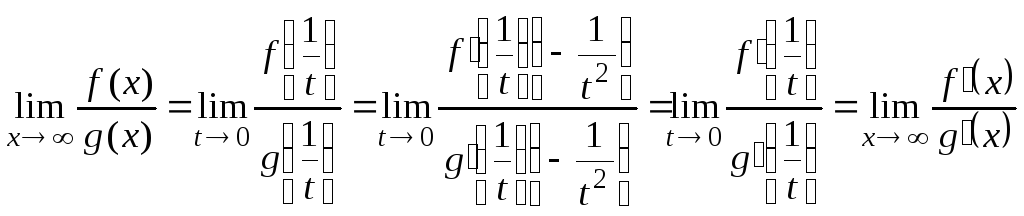С помощью правило Лопиталя можно раскрывать и другие виды неопределенностей

1) , 2), 3),

4) , 5), 6).

Правило Лопиталя для неопределенности схематически обосновывается так

.

Таким образом

.

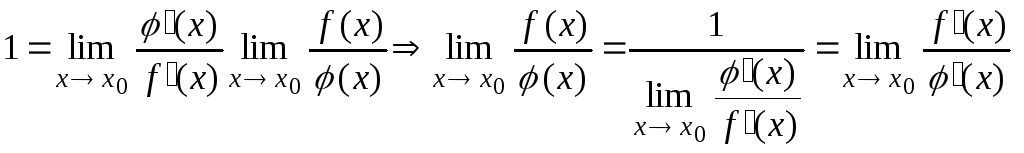Неопределенности ираскрываются с помощью простых алгебраических преобразований

.

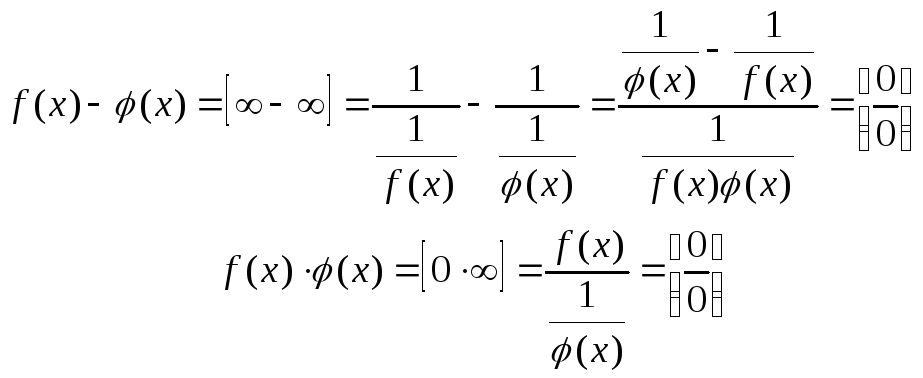Неопределенности вида ,,приводятся к рассмотренным методом логарифмирования.

Рассмотрим этот алгоритм на примере

.
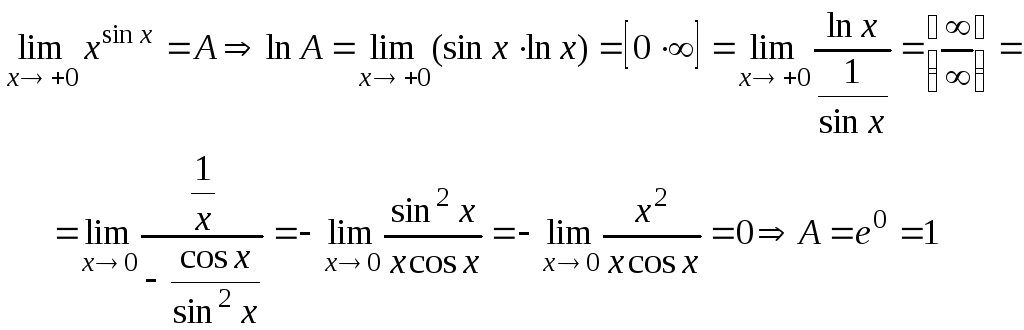