
- •Часть 3
- •Глава 1
- •1.1. Алгебраическая форма комплексного числа
- •Задачи для самостоятельного решения
- •1.2 Тригонометрическая форма комплексного числа
- •Задачи для самостоятельного решения
- •1.3. Показательная форма комплексного числа
- •1.4. Понятие о функции комплексного переменного
- •Задачи для самостоятельного решения
- •1.5. Основные элементарные функции комплексной переменной
- •1.6. Производная функции комплексной переменной и понятие аналитичности
- •1.7. Интегрирование функций комплексной переменной
- •Задачи для самостоятельного решения
- •Глава 2
- •2.1.Оригиналы и изображения. Преобразование Лапласа.
- •2.2. Свойство линейности
- •2.3. Свойство подобия
- •2.4. Дифференцирование изображения.
- •2.5. Теорема смещения
- •2.6. Дифференцирование оригинала
- •2.7. Решение линейных дифференциальных уравнений с постоянными коэффициентами
- •Задачи для самостоятельного решения
1.6. Производная функции комплексной переменной и понятие аналитичности
Производной
функции
![]() в точке
в точке![]() называется предел отношения приращения
функции
называется предел отношения приращения
функции![]() к приращению аргумента
к приращению аргумента![]() при
стремлении
при
стремлении ![]() к нулю:
к нулю:
|
|
(1.18) |
Если этот предел
существует при
![]() по произвольному пути, то функция
называется дифференцируемой в точкеz. Если функция
по произвольному пути, то функция
называется дифференцируемой в точкеz. Если функция![]() дифференцируема во всех точках области
дифференцируема во всех точках области![]() ,
то она называется аналитической в этой
области.
,
то она называется аналитической в этой
области.
Теорема: если
функция![]() имеет непрерывные частные производные,
то для аналитичности функции в этой
области необходимо и достаточно
выполнение условий
имеет непрерывные частные производные,
то для аналитичности функции в этой
области необходимо и достаточно
выполнение условий
|
|
(1.19) |
Докажем необходимость этих условий. Рассмотрим предел

По условию функция
![]() является аналитической, поэтому этот
предел не зависит от пути, по которому
является аналитической, поэтому этот
предел не зависит от пути, по которому![]() .
.
Пусть сначала
![]() ,
а затем
,
а затем![]() ,
тогда
,
тогда
|
|
(1.20) |
Пусть теперь
сначала
![]() ,
а затем
,
а затем![]() ,
тогда
,
тогда
|
|
(1.21) |
В силу аналитичности
функции
![]() выражения
(1.20) и (1.21) равны. Приравнивая их
действительные части, получим первое
равенство (1.19), а равенство мнимых частей
приводит ко второму соотношению (1.19).
Достаточность условий (1.19)
примем без доказательства.
выражения
(1.20) и (1.21) равны. Приравнивая их
действительные части, получим первое
равенство (1.19), а равенство мнимых частей
приводит ко второму соотношению (1.19).
Достаточность условий (1.19)
примем без доказательства.
Соотношения (1.19) называются условиями Коши - Римана (иногда их так же называют условиями Даламбера - Эйлера).
Проверим
выполнение условий (1.19) для функции
![]() .
.
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Оба условия (1.13) выполняются, поэтому показательная функция является аналитической. Аналогично можно доказать аналитичность всех остальных основных элементарных функций. То же относится ко всем вообще элементарным функциям, т.е. к функциям, которые составляются из основных элементарных с помощью конечного числа арифметических операций и операции взятия функции от функции.
Пример 1.21.
1)![]() - элементарная функция, следовательно
она является аналитической всюду, кроме
точки
- элементарная функция, следовательно
она является аналитической всюду, кроме
точки![]() ,
в которой эта функция не определена.
,
в которой эта функция не определена.
2)![]() -
функция не аналитическая:
-
функция не аналитическая:![]() ,
,![]() ,
условия (1.19) не выполняются.
,
условия (1.19) не выполняются.
Дифференцирование функций комплексного переменного
При выводе условий (1.19) были получены две формулы вычисления производной
|
|
(1.22) |
|
|
(1.23) |
Рассмотрим функцию
![]() .
.
Найдем ее производную
по формуле (1.22):
![]() .
.
![]() ,
,
![]() ,
,![]() .
.
Аналогично можно показать, что справедливы все формулы и правила дифференцирования, известные из теории функций действительного переменного:
![]() ,
,
![]() ,
, , , .
,
, , , .
1.7. Интегрирование функций комплексной переменной
Пусть Lнекоторый контур в комплексной плоскости,![]() функция комплексной переменнойz,
а функции двух действительных переменных
функция комплексной переменнойz,
а функции двух действительных переменных![]() и
и![]() являются соответственно действительной
и мнимой частью функции
являются соответственно действительной
и мнимой частью функции![]() ,
то
,
то
|
|
(1.24) |
где
![]() ,
,![]() ,
,![]()
![]() .
.
Это формула для вычисления интеграла по контуру.
Оба интеграла являются криволинейными интегралами второго рода в действительной плоскости.
Итак, вычисление интегралов по контуру сводится к вычислению двух криволинейных интегралов в действительной плоскости.
Пример 1.22
Вычислить
интеграл
![]() ,L- отрезок прямой между
точками
,L- отрезок прямой между
точками
![]() и
и
![]() +1.
+1.
Решение
![]()
![]()
![]()
Теорема Коши для односвязной области
Если функция
![]() является аналитической в замкнутой
односвязной областиD
, то интеграл от нее по любому замкнутому
контуру, расположенному в областиD,
равен нулю:
является аналитической в замкнутой
односвязной областиD
, то интеграл от нее по любому замкнутому
контуру, расположенному в областиD,
равен нулю:![]() .
.
Доказательство:
Пусть функция
![]() аналитическая в областиD.
Тогда для нее выполняютcя
условия Коши-Римана (1.19)
аналитическая в областиD.
Тогда для нее выполняютcя
условия Коши-Римана (1.19)
|
|
(1.25) |
Вспомним условие
равенства нулю криволинейного интеграла
второго рода
![]() по любому замкнутому контуру
по любому замкнутому контуру
|
|
(1.26) |
тогда первое условие (1.19) обращает в ноль второй интеграл в правой части равенства (1.25), а второе условие (1.19) – первый. Что и требовалось доказать.
Можно доказать, что для аналитической функции интеграл по контуру зависит только от начальной и конечной точек интегрирования. Более того, для аналитической функции имеет место формула Ньютона-Лейбница
|
|
(1.27) |
где
![]() -
первообразная аналитической функции
-
первообразная аналитической функции![]() .
.
Пример 1.23
Вычислить интеграл
![]() .
.
Решение
Подынтегральная
функция![]() является аналитической. Воспользуемся
формулой Ньютона-Лейбница (1.27),
получим
является аналитической. Воспользуемся
формулой Ньютона-Лейбница (1.27),
получим
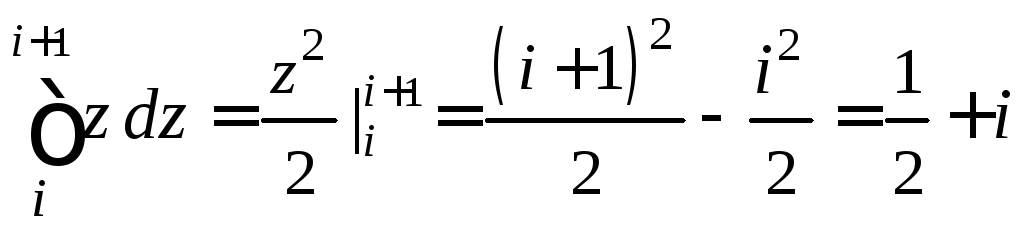 .
.

 ,
,