ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 7. Алгоритмы и методы анализа статических режимов ССУ в интегрированных САПР

разреженности). Поэтому при создании специализированных САПР необходимы предварительный анализ особенностей ММ заданного класса задач (значений n, z, допустимых погрешностей) и соответствующий выбор конкретного метода. При создании универсальных САПР необходима реализация средств адаптации метода решения к конкретным условиям. Такая адаптация чаще всего применяется в рамках методов установления или продолжения решения по параметру.

Таким образом, алгоритмы и методы анализа статических режимов СУ в современных САПР есть прежде всего алгоритмы и методы решений линейных и нелинейных алгебраических уравнений математической модели СУ для разных уровней описания систем. При этом применение традиционных частотных методов анализа устойчивости и качества трансформируется в обработку результатов численного решения систем ЛАУ. Например, в широко применяемом формате Spice проектировщику для получения наглядных характеристик системы ЛАХ и ФЧХ достаточно ввести эквивалентную схему замещения устройства или СУ, выполнить анализ частотных характеристик (расчет системы ЛАУ ММ устройства или СУ) и вывести графические результаты моделирования с использованием правил языка проектирования.

Лекция8. АлгоритмыиметодыанализаССУ вовременнойобластивинтегрированныхСАПР

Методы анализа СУ во временной области. Методы анализа СУ с «жесткими» системами уравнений. Основные характеристики методов анализа СУ во временной области. Алгоритмы автоматического выбора шага. Выбор эффективных методов анализа переходных процессов СУ.

МетодыанализаСУвовременнойобласти

Анализ временных оценок качества СУ осуществляется численными методами решения системы уравнений ММ, которая может быть представлена: в виде системы дифференциальных уравнений в неявной форме

dV			0 ; в виде системы дифференциальных уравнений в явной фор-
F	dt	,V ,t
ме	dV	F(V ,t) , где V– вектор фазовых переменных размерностью n.
	dt

По исходной ММ СУ строится переходный процесс в системе, по которому и делаются нужные оценки [5; 6].

Анализ переходных процессов проектируемого объекта сводится к численному интегрированию системы ОДУ и нахождению V(t) на заданном интервале времени [0, Ткон], при заданных начальных условиях V(0)=V0. При

 Автоматизированное проектирование средств и систем управления. Курс лекций

112

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 8. Алгоритмы и методы анализа ССУ во временной области в интегрированных САПР

решении этой задачи на интервале интегрирования выделяется конечное число точек tk, в которых определяются значения V, к = 1, 2, …, Ш, где Ш – число шагов интегрирования [7].

В каждой точке tk система ОДУ представляется в виде системы n алгебраических уравнений с 2n неизвестными. Система уравнений дополняется уравнениями, задаваемыми выбранным методом численного интегрирования.

Обобщенная формула методов интегрирования используется для решения систем ОДУ.

Vk G(Vk ,Vk 1,..,Vk p ,Vk 1,Vk 2,..,Vk p ) ,

(8.1)

где G – некоторая функция, определяемая способом построения метода интегрирования (чаще всего линейная); p – количество предыдущих точек, использованных в формуле интегрирования (порядок метода); – коэффициент.

Если уравнения составляются для текущего к-го момента времени ( = 0), то метод явный (иначе, экстраполяционный метод, основанный на формулах интегрирования вперед).

Если уравнения составляются для следующего (к+1)-го момента времени ( = 1), то метод неявный (интерполяционный, основанный на формулах интегрирования назад).

Различия между ними удобно показать на примере простейших методов первого порядка – методов Эйлера. Формула явного метода Эйлера представляет собой следующую формулу замены производных в точке tn:

dV / dt | n (Vn 1 Vn ) / hn ,

где индекс равен номеру шага интегрирования; hn = tn+1 – tn – размер шага интегрирования (обычно hn называют просто шагом интегрирования). В формуле неявного метода Эйлера использовано дифференцирование назад:

dV / dt | n (Vn Vn-1 ) / hn ,

где hn tn tn-1.

В зависимости от значения р методы интегрирования распадаются на два класса: 1) одношаговые, если р = 1; 2) многошаговые, если р > 1, причем р называют порядком многошагового метода (в формуле интегрирования используют результаты предыдущих шагов).

Классификацияосновныхчисленных методоврешениясистемОДУ

 Автоматизированное проектирование средств и систем управления. Курс лекций

113

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 8. Алгоритмы и методы анализа ССУ во временной области в интегрированных САПР

1)Явные:

– блочные,

– одношаговые,

•многоэтапные методы Рунге – Кутты,

•одноэтапные:

–метод Эйлера,

–метод разложения в ряд Тейлора,

– многошаговые:

•метод Адамса – Башфорта,

•методы с сериями шагов.

2)Неявные:

–одно- и двушаговые:

•метод Эйлера,

•метод трапеций.

•Рунге – Кутты

–многошаговые:

•ФДН,

•Адамса – Мултона,

–блочные.

Всовременных САПР для решения систем ОДУ применяются наиболее распространенные методы ФДН (формулы дифференцирования назад), Адамса и Рунге – Кутты.

Общий вид формул дифференцирования назад:

								p
						dVk		ai Vk i
								i 0	,
						dt		hk
h	t	k	t	k -1	– величина k-го шага интегрирования; аi – коэффициент (значе-
k

ние зависит от порядка метода р).

Аппроксимация производных в точке tk производится с помощью значений, относящихся к данному и предыдущему моментам времени. При р = 1 формула метода ФДН совпадает с неявной формулой Эйлера

Vk (Vk hVk 1) . k

Часто используют формулу Гира второго порядка, называемую формулой Шихмана при h = const

V		3	V	2 V		1	V		/ h.
		2				2
k			k	k 1			k 2
 Автоматизированное проектирование средств и систем управления. Курс лекций										114

методами интегрирования, основанными на представлении производной

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 8. Алгоритмы и методы анализа ССУ во временной области в интегрированных САПР

Формулы интегрирования при р > 1 в явных методах Адамса имеют

вид

	V		a1 (Vk Vk 1)		p	a	V	,
	k 1		hk		i 2	i	k i

неявных методах Адамса:

	V		a0 (Vk Vk 1)		p 1	a	V
									i	,
	k		hk		i 1	i	k

явная формула Адамса при р = 1 называется явной формулой Эйлера:

Vk 1 (Vk hVk 1) , k

при р = 2 метод Адамса называют методом трапеций:

Vk 2 (Vk hVk 1) Vk 1. k

Методы ФДН являются наиболее распространенными современными dV

dt

в точке tk через значения Vk и i-ю предысторию, т. е. в точках Vk-1, Vk-2, …,Vk-i. Их основное преимущество перед другими методами – возможность смены

не только шага интегрирования h, но и порядка метода р, что обеспечивает высокую точность расчетов характеристик.

Явные методы интегрирования целесообразно использовать при решении систем ОДУ в форме Коши. Достоинства явных методов: малый объём вычислений на одном шаге; уменьшение затрат памяти. Явные методы наиболее легко реализуются, приводят к сравнительно небольшому объему вычислений на одном шаге интегрирования. Однако для соблюдения условий устойчивости приходится уменьшать шаг настолько, что увеличившееся число шагов может сделать недопустимо большими общие затраты машинного времени. Поэтому явные методы, к которым относятся известные методы Адамса – Башфорта и явные варианты метода Рунге – Кутта, оказываются малонадежными и в САПР находят ограниченное применение.

Чаще всего используется формула, предложенная Рунге, основанная на вычислении приближенного решения y1 в узле x0 + h в виде линейной комбинации с постоянными коэффициентами:

 Автоматизированное проектирование средств и систем управления. Курс лекций

115

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 8. Алгоритмы и методы анализа ССУ во временной области в интегрированных САПР

y1	y1	pq1k1 (h) pq2 k2 (h) ... pqq kq (h)		(8.2)
			,
			k 1 ( h ) f ( x 0 , y 0 ) ,
		k2 (h) hf (x0 h, y0 21k1 (h))
			,
			…………………..
	kq (h) hf (x0		q h, y0 q1k1 (h) ... q,q 1kq 1	(h))
				.

Существует семейство формул типа Рунге – Кутта (8.2) четвертого порядка точности, для которых q = s = 4. Формула классического метода Рунге – Кутта

y1 y0 16 (k1 2k2 2k3 k4 ), k1 hf (x0 , y0 ),

k2 hf (x0 12 h, y0 12 k1), k3 hf (x0 12 h, y0 12 k2 ), k4 hf (x0 h, y0 k3 ).

МетодыанализаСУс «жесткими» системамиуравнений

Особая группа – задачи с «жесткими» системами уравнений (чаще всего это системы дифференциальных уравнений высокого порядка, описывающие динамические системы). Для описания процесса нужно использовать функции двух типов: на малых отрезках – функции с быстро меняющимися параметрами (большие производные) и на остальной части – функции с малыми производными (медленные движения). Часто в системе ОДУ не удается явно выделить члены с малыми параметрами, однако решение также имеет участки быстрых и медленных движений.

В частности, система ОДУ будет плохо обусловленной (жесткой), если выполняется условие

max( i )

	z	i	1,	(8.3)
		min( i )

i

где z – число обусловленности матрицы А. Обычно математическую модель считают плохо обусловленной (а систему уравнений жесткой), если z > 105.

 Автоматизированное проектирование средств и систем управления. Курс лекций

116

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 8. Алгоритмы и методы анализа ССУ во временной области в интегрированных САПР

Метод Гира для жестких систем является многошаговым предсказы- вающе-исправляющим ФДН методом. При этом формула-предиктор и фор- мула-корректор имеют один и тот же порядок.

Когда система уравнений является жесткой, интегрирование осуществляется специальным методом на основе формул дифференцирования назад (ФДН) вида

k

xm 1 ai xm 1 i hbfm 1 .

i 1

Вметоде Гира эти формулы реализованы с помощью вектора Нордсика, позволяющего использовать эффективный алгоритм автоматического изменения порядка и величины шага. Последние компоненты вектора Нордсика

позволяют получить оценку ошибки. При k = 1 (тогда a1 = b = 1) получим не-

явный Эйлера – метод 1-го порядка.

Многошаговые формулы основаны на численном интегрировании, т. е. интеграл аппроксимируется с помощью какой-либо квадратурной формулы. Существуют многошаговые методы, воплотившие совсем другую идею – численного дифференцирования искомой функции. Рассмотрим вывод формул численного интегрирования для жесткой системы. Метод Гира строится на основе формул дифференцирования назад

k
i yn i h k f (xn k , yn k ) 0	, k	1.	(8.4)

i 0

Предположим, что начальное приближение для решения уравнения (8.4) находится по явной формуле вида

	k 1
yn k	i yn k h k 1 f (xn k 1 , yn k 1 ) .	(8.5)

i 0

Обозначим m n k и перепишем формулу (8.5) в следующем виде:

k
ym k i ym i		h k 1 f (xm 1 , ym 1 ) .	(8.6)
i 0
Обозначим Ai k i ,	B1 k 1	и заменим m на n. Тогда

k

yn Ai yn i hB1 f (xn 1 , yn 1 ) .

i 0

Аналогично преобразуем формулу (8.4):

 Автоматизированное проектирование средств и систем управления. Курс лекций

117

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 8. Алгоритмы и методы анализа ССУ во временной области в интегрированных САПР

k

ym k i ym i h k f (xm , ym ) . i 0

Обозначим i k i , b0 k и заменим m на n. Тогда

k

yn i yn i hb0 f (xn , yn ) .

i 0

Рассмотрим следующий итерационный процесс:

	k
	yn(0) Ai yn i hB1		fn 1 ,	(8.7)
	i 0
yn(v 1)	k
	i yn i hb0	f (xn , yn	(v) ), v 0,1,2,... .	(8.8)

i 0

Из (8.8) получаем

yn(v 1) yn(v) b0 hf xn , yn(v) hf xn , yn(v 1) , v 1,2,... .

Определим v-е приближение для производной hy (xn ) по формуле

hyn	hf xn , yn	,
(v)	(v 1)

погрешность этого приближения для hy (xn ) имеет порядок O(h

yn	yn	b0	hf xn , yn	hyn	,	v 1,2,... .
(v 1)	(v)		(v)	(v)

Вычтем (8.7) из (8.8) при v = 0:

k

yn(1)

yn(0)

( i Ai ) yn i

hb0 f (xn , yn(0) ) hB1 fn 1

i 1

k

y

(0) b

, y(0) )

( Ai i )

y

h

B1

f

hf (x

n

i

.

n

0

n

b

n

b

n 1

i 1

0

0

(8.9) k 2 ) . Тогда

(8.10)

Обозначим i (Ai i )b0 , 1 B1 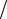b0 и определим начальное приближение для производной hy (xn ) по формуле

hyn(0)	k
	i yn i h 1	fn 1 .	(8.11)

i 1

 Автоматизированное проектирование средств и систем управления. Курс лекций

118

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 8. Алгоритмы и методы анализа ССУ во временной области в интегрированных САПР

Погрешность этого приближения к hy (xn ) имеет порядок O(hk 1 ) . Тогда (8.10) примет вид

yn(1) yn(0) b0 hf xn , yn(0)			hyn(0)		.			(8.12)
Из (8.12) следует, что формула yn			yn	b0 hf xn , yn		hyn		справедли-
ва также для v = 0. При этом hyn	(v	1)	(v)		(v)		(v)
	определяется с помощью (8.11).
(0)
Введем в рассмотрение векторы
Yn ( yn , hyn , yn 1 ,..., yn k 1 )T
и
Y (xn ) ( y(xn ),hy (xn ), y(xn 1 ),..., y(xn k 1 ))T .
Первая компонента yn вектора Yn		аппроксимирует y(xn ) , вторая компо-
					Остальные компоненты yn l
нента hyn вектора Yn аппроксимирует		hy (xn ) .

аппроксимируют значения точного решения y(xn l ) ,												l 1,2,..., k 1. Определим
также вектор
Yn	( yn				,hyn			, yn 1,..., yn k 1 )
(v)			(v)			(v)					T
и матрицу
	A			B			A ...		A	A
		1			1		2		k 1		k
	1			1		2 ...			k 1	k
		1		0			0 ...		0	0
D												.
		0		0			1 ...		0	0
	. .						. ... .			.
		0		0			0 ...		1	0

Тогда предсказывающие формулы (8.7) и (8.11) для решения y(xn ) и производной hy (xn ) могут быть представлены в виде следующего векторного соотношения:

				Yn(0) DYn 1 .							(8.13)
	Погрешность первой и второй компоненты вектора									имеет порядок
									Y (0)
O(hk 1 ) , а для остальных равна нулю, если y						y(x			n
					n i		n i	) , i 1,..., k 1, и O(hk 2 ) ,
если	y(x	) y	n i	O(hk 2 ) . Значит,
	n i
	 Автоматизированное проектирование средств и систем управления. Курс лекций										119

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 8. Алгоритмы и методы анализа ССУ во временной области в интегрированных САПР

Y (xn ) Yn(0) O(hk 1 ) .

Из (8.9) следует, что

hyn	hyn	hf (xn , yn	) hyn	.
(v 1)	(v)	(v)	(v)

Введем вектор c (b0 ,1,0,...,0)T и функцию невязки

F (Yn	) hf (xn	, yn	) hyn	.
(v)		(v)	(v)

Тогда исправляющие формулы (8.9) и (8.15) для решения водной hy (xn ) могут быть представлены в виде

Yn(v 1) Yn(v) cF(Yn(v) ) .

(8.14)

(8.15)

(8.16)

y(xn ) и произ-

(8.17)

Погрешность первой компоненты вектора Yn(v 1) имеет порядок O(hk 1 ) , по-

грешность второй компоненты – O(hk 2 ) , а для остальных компонент погреш-
ность такая же, как для Y (0) . Значит,
n
Y (xn ) Yn(v 1)	O(h k 1 ) .	(8.18)

Итерационный процесс (8.7), (8.8) сходится к yn , если h достаточно мало. Следовательно, будет сходиться итерационный процесс (8.13), (8.17):

Y (v) Y

n

n

и

Y (xn ) Yn O(hk 1 ) .

Определим линейное преобразование Q, которое переводит вектор Y (xn )

в вектор Z (xn ) O(hk 1 ) , где

h

2

h

k

y

(k )

(xn )

T

y (xn )

,...,

,

Z (xn ) y(xn ), hy (xn ),

2

k!

т. е.

QY (xn ) Z (xn ) O(h k 1 ) ,

 Автоматизированное проектирование средств и систем управления. Курс лекций

120

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 8. Алгоритмы и методы анализа ССУ во временной области в интегрированных САПР

или записывается покомпонентно,

y(xn )

y(xn )

hy (xn )

hy (xn )

h 2 y (xn )

y(xn 1 )

2

Q

h

.

2 y (xn )

y(x

n

2

)

6

...

...

k

y

(k )

(xn

)

y(xn k 1 )

h

k!

ВекторZ (xn ) называется вектором Нордсика. Преобразование Q переводит вектор Y (xn ) в векторZ (xn )

Zn QYn Q(Y (xn ) O(hk 1 )) QY (xn ) O(hk 1 ) Z (xn ) O(hk 1 ) .

Матрицу Q такого преобразования можно найти следующим образом. Так как преобразование Q не меняет первые две компоненты вектора, то первые две строки матрицы Q имеют вид

1 0 0 . . . 0

0 1 0 . . . 0

Чтобы найти l-ю строку матрицы Q

ql1, q21,..., qlk 1 l 3 ,

надо разложить все слагаемые в левой части равенства

	ql1 y xn ql 2 hy xn	ql 3 y xn 1	... ql ,k 1 y xn k 1		hl 1 y l 1 xn		O hk 1
					l 1 !

по степеням h, а затем приравнять коэффициенты при одинаковых степенях h справа и слева. Получим k + 1 уравнений с k + 1 неизвестными. Решая эту систему, найдем элементы l-й строки. Таким способом находятся строки третья, четвертая, …, (k+1)-я.

Если записать покомпонентно, то имеем

 Автоматизированное проектирование средств и систем управления. Курс лекций

121

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 8. Алгоритмы и методы анализа ССУ во временной области в интегрированных САПР

y(x )

y(x

)

n

hy (xn )

n

hy (xn )

h2 y (xn )

y(xn 1 )

2

Q

2

O(h

k 1

) .

h

y (xn )

y(xn 2 )

6

...

...

y(x

)

hk y(k ) (xn )

n k

1

k!

Из (8.18) следует, что

Zn(v) QYn(v) Q(Y (xn ) O(hk 1 )) QY (xn ) O(hk 1 ) Z (xn ) O(hk 1 ) .	(8.19)
Применим преобразование Q к (8.13). Тогда
QYn(v 1) QYnv QcF(Yn(v) ) Zn(v) IF(Yn(v) ) ,
где I Qc (l0 ,l1 ,l2 ,...,lk )T . Так как функция невязки F(Yn(v) ) зависит	только от

первых двух компонент вектора Yn(v) , а преобразование Q первые две компоненты не меняет, то эти компоненты вектора Yn(v) совпадают с первыми двумя компонентами вектора Zn(v) . Поэтому

	Zn(v 1) Zn(v) IF(Zn(v) ) .
Из сходимости Y (v)	к Y следует сходимость Z	(v) кZ	n	. Таким образом,
n	n	n
приходим к такому сходящемуся итерационному процессу:
	Zn(0) PZn 1 ,
Zn(v 1)	Zn(v) IF(Zn(v) ) , v 0,1,... .			(8.20)
Из (8.20) следует, что
Zn(v 1) Zn(0) I F (Zn(0) ) F (Zn(1) ) ... F (Zn(v) ) .				(8.21)

Из сходимости (8.21) вытекает, чтоZn(v 1) сходится к

Zn Zn(0) Iw ,

(8.22)

 Автоматизированное проектирование средств и систем управления. Курс лекций

122

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 8. Алгоритмы и методы анализа ССУ во временной области в интегрированных САПР

где		v
	w lim F(Znj ) , причем, как следует из (8.21),
	v	j 0
		F(Zn ) 0 .	(8.23)
	Подставляя (8.22) в (8.23), получаем уравнение
		F(Zn(0) Iw) 0 .	(8.24)

Решение уравнения (8.24) относительно w методом Ньютона приводит:

1

F(Z (0) Iw(v) )

1

wv

wv

n

I

F Zn(0) Iwv

.

Z

Умножим обе части равенства на I:

(0)

Iw

(v)

)

1

Iw

v 1

Iw

v

F(Zn

(0)

Iw

v

.

I

Z

I

F Zn

Прибавим к обеим частям равенства Zn(0)

и обозначим Zn(v) Zn(0) Iw(v) .

Тогда имеем следующий итерационный процесс:

Zn(0)

или

	1)	F(Z		(v) )	1
Zn(v		Zn(v) I		n	I	F(Zn(v) ) .
			Z

Начальное приближение для этого процесса определяется с помощьюPZn 1 . Из (8.16) находим

F

F

F

F

f

,

2

,...,

k 1

, 1,0,...,0

Z

Z

Z

Z

h

y

.

Обозначим
F(Zn(v) )		1		f (xn , yn(v) )	1
W		I
	Z		hl0	y	l1 .
Тогда
Zn(v 1) Zn(v) IWF(Zn(v) ),					(8.25)

			(v)	)		1
(v 1)	(v)		f (xn , yn				(v)		(v)	.
Zn	Zn	I hl0	y		l1		hf (xn , yn	) hyn

 Автоматизированное проектирование средств и систем управления. Курс лекций

123

(v) n

(v) n

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 8. Алгоритмы и методы анализа ССУ во временной области в интегрированных САПР

Итерационный процесс (8.25) отличается от итерационного процесса (8.20) тем, что сложению вектора IFcZ в (8.20) предшествует умножение F

на матрицу W в (8.25) и только после этого производится коррекция значения Z .

Если правая часть дифференциального уравнения f (x, y) линейна по y,

то итерационный процесс (8.25) сойдется за одну итерацию.

Компоненты вектора I (l0 ,l1 ,...,lk )T для методов разного порядка аппроксимации приведены в табл. 8.1.

															Таблица 8.1
Коэффициенты метода Гира						I (l	0	,l ,...,l			k	)T
								1
				Порядок метода
Коэффициенты	2	3				4						5			6
l0	2		6			12							60		20
	3	11					25					137			49
l1	1	1					1					1			1
l2	1		6				7					225			58
	3	11					10					274			63
l3			1				1						85					5
		11					5					274			12
l4							1						15				25
							50					274			252
l5													1					1
												274			84
l6																1
															1764

Рассмотренный метод решения жестких систем на основе формул дифференцирования назад (метод Гира) позволяет получать эффективные алгоритмы расчетов за счет реализации процедур автоматической смены порядка и шага метода, по сравнению с другими методами решения жестких систем.

 Автоматизированное проектирование средств и систем управления. Курс лекций

124