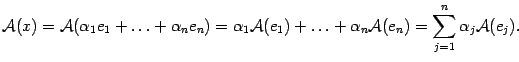- •Решение матричных уравнений
- •Линейные пространства
- •Линейные подпространства
- •Действия с линейными преобразованиями. Произведение линейного преобразования на число.
- •Сложение и вычитание линейных преобразований.
- •Умножение линейных преобразований.
- •Норма вектора
- •Формулировка
- •Комментарии
- •Примеры
- •Доказательство
- •Квадратичные формы
- •Уравнения поверхностей второго порядка
Линейные подпространства
Рассмотрим некоторое подмножество X1 линейного пространства X , т.е. X1 Н X .
Определение. Подмножество X1 линейного пространства X называется линейным подпространством, если для любых векторов x, y О X1 и любого числа α :
x + y О X1 ;
αx О X1 .
Рассмотрим два линейных подпространства X1 и X2 линейного пространства X .
Если любой вектор x О X может быть единственным образом представлен в виде x = x1 + x2 , где x1 О X1 и x2 О X2 , то говорят, что пространство X разложено впрямую сумму подпространств X1 и X2 .
Прямая сумма обозначается X = X1 + X2 .
Любое линейное пространство может быть разложено в прямую сумму нескольких подпространств. В частности, разложение вектора по базису связано с разложением n–мерного пространства в прямую сумму n одномерных подпространств.
Я НЕ НАШЕЛ «ПОДПРОСТРАНСТВА ПРОСТРАНСТВА R3»
№26
Матрица линейного преобразования
В
примере
19.4 было
показано, что преобразование ![]() -мерного
пространства, заключающееся в умножении
координатных столбцов векторов на
фиксированную матрицу, является линейным
преобразованием. В этом разделе мы
покажем, что все линейные
преобразования конечномерного
пространства устроены таким же образом.
-мерного
пространства, заключающееся в умножении
координатных столбцов векторов на
фиксированную матрицу, является линейным
преобразованием. В этом разделе мы
покажем, что все линейные
преобразования конечномерного
пространства устроены таким же образом.
Пусть ![]() --
-- ![]() -мерное
линейное пространство, в котором задан
базис
-мерное
линейное пространство, в котором задан
базис ![]() ,
, ![]() --
линейное преобразование. Возьмем
произвольный вектор
--
линейное преобразование. Возьмем
произвольный вектор ![]() .
Пусть
.
Пусть 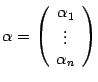 --
его координатный столбец. Координатный
столбец вектора
--
его координатный столбец. Координатный
столбец вектора ![]() обозначим
обозначим ![]() .
.
Запишем
разложение вектора ![]() по
базису пространства
по
базису пространства ![]() .
Для образа этого вектора получим
.
Для образа этого вектора получим
|
|
(19.2) |
Векторы ![]() имеют
какие-то координатные столбцы, обозначим
их
имеют
какие-то координатные столбцы, обозначим
их 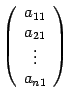 ,
, 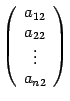 ,
...,
,
...,  соответственно.
В этой записи первый индекс показывает
номер координаты, а второй индекс --
номер вектора. Соответственно,
соответственно.
В этой записи первый индекс показывает
номер координаты, а второй индекс --
номер вектора. Соответственно,
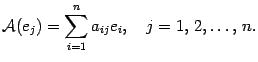
Подставим это выражение в равенство (19.2) и, используя предложение 14.3, изменим порядок суммирования
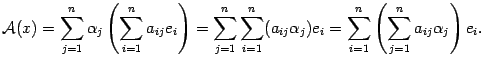
Это
равенство означает, что ![]() -той
координатой вектора
-той
координатой вектора ![]() служит
служит 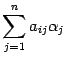 .
.
Составим
матрицу ![]() из
координатных столбцов векторов
из
координатных столбцов векторов ![]() ,
...,
,
..., ![]()

Вычислим
произведение матрицы ![]() на
столбец
на
столбец ![]()

Мы
видим, что ![]() -ый
элемент столбца совпадает с
-ый
элемент столбца совпадает с ![]() -ой
координатой вектора
-ой
координатой вектора ![]() .
Поэтому
.
Поэтому
|
|
(19.3) |
Это означает, что в выбранном базисе действие любого линейного преобразования сводится к умножению матрицы на координатный столбец вектора.
Матрица ![]() называется матрицей
линейного преобразования
называется матрицей
линейного преобразования ![]() .
Еще раз напомним, как она составлена:
первый столбец является координатным
столбцом образа первого базисного
вектора, второй столбец -- координатным
столбцом образа второго базисного
вектора и т.д.
.
Еще раз напомним, как она составлена:
первый столбец является координатным
столбцом образа первого базисного
вектора, второй столбец -- координатным
столбцом образа второго базисного
вектора и т.д.
Пример 19.5
Найдем матрицу линейного преобразования ![]() из
примера
19.1.
из
примера
19.1.
Выберем
какой-нибудь базис ![]() .
Тогда
.
Тогда
![]()
Следовательно,
первый столбец матрицы ![]() имеет
вид
имеет
вид 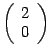 .
Аналогично
.
Аналогично
![]()
Второй
столбец матрицы ![]() имеет
вид
имеет
вид 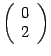 .
В итоге
.
В итоге

Пример 19.6
Найдем матрицу линейного преобразования ![]() из
примера
19.2.
Угол
из
примера
19.2.
Угол ![]() возьмем
равным
возьмем
равным ![]() .
В качестве базиса возьмем привычный
ортонормированный базисi, j.
.
В качестве базиса возьмем привычный
ортонормированный базисi, j.
Из
рисунка 19.7 видно, что вектор ![]() имеет
координаты
имеет
координаты ![]() и
и ![]() .
.
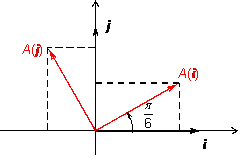
Рис.19.7.Координаты образов базисных векторов при преобразовании поворота
Поэтому
координатный столбец образа первого
базисного вектора имеет вид 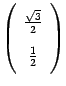 .
Координаты образа второго базисного
вектора равны
.
Координаты образа второго базисного
вектора равны ![]() и
и ![]() ,
его координатный столбец имеет вид
,
его координатный столбец имеет вид 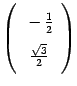 .
В итоге получаем, что в базисе i, j матрица
поворота на угол
.
В итоге получаем, что в базисе i, j матрица
поворота на угол ![]() имеет
вид
имеет
вид
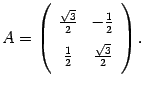
№26