Плоскопараллельное движение твердого тела

Плоскопараллельным называется такое движение твердого тела, при котором все его точки движутся в плоскостях, параллельных некоторой неподвижной плоскости.

Характерным примером плоскопараллельного движения является качение цилиндра (катка) по неподвижной плоскости, все сечения которого параллельные некоторой неподвижной плоскости (например, стене дома), будут двигаться одинаково. Исследование плоскопараллельного движения сводится к исследованию движения одного сечения тела в своей плоскости, которое называют плоским.

При плоском движении в каждый данный момент времени существует единственная точка Р плоской фигуры, скорость которой равна нулю (мгновенный центр скоростей), а распределение скоростей таково, как если бы плоская фигура совершала вращательное движение вокруг мгновенного центра скоростей (теорема о мгновенном центре скоростей):

V =   h, (3.5)

где h – расстояние от точки до мгновенного центра скоростей,  – угловая скорость плоской фигуры.

На рис. 3.3 показаны способы нахождения мгновенного центра скоростей по скоростям двух точек плоской фигуры. На рис. 3.3, а) показан случай, когда известен вектор скорости точкиА и прямая, по которой направлен вектор скорости точки В. Мгновенный центр скоростей находится на пересечении перпендикуляров к скоростям, восстановленным в этих точках.

Угловая скорость  в этом случае находится по известной величине скорости V_A точки А:

. (3.6)

В случае, показанном на рис. 3.3, б, угловую скорость плоской фигуры можно найти, пользуясь свойством пропорции, по одной из формул

.

Аналогично, в случае, показанном на рис. 3.3, в, угловую скорость можно определить по формулам

.

В случае, когда скорости двух точек А и В плоской фигуры параллельны, но не перпендикулярны к АВ (рис. 3.3, г), мгновенный центр скоростей находится в бесконечности и, следовательно, угловая скорость равна нулю. Векторы скоростей всех точек плоской фигуры в данный момент времени будут равны. Движение плоской фигуры в этом случае называют мгновенно поступательным.

а)

б)

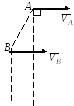
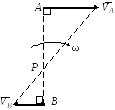
в)

г)

Рис. 3.3

3.2. Указания к выполнению контрольной задачи к2

Задача К2 – на определение угловых скоростей звеньев и скоростей отдельных точек плоского многозвенного механизма, состоящего из 4 стержней и ползуна В, соединенных друг с другом и неподвижными опорами с помощью шарниров. Стержни 1 и 4 совершают вращательное движение, ползун В – поступательное, стержни 2 и 3 – плоское движение в своей плоскости.

Поступательным движением плоской фигуры является движение, при котором любая прямая, проведенная в плоскости движущейся фигуры, остается параллельной самой себе.

Вращательным движением плоской фигуры в своей плоскости является такое ее движение, при котором одна точка фигуры (центр вращения) остается все время неподвижной. Траекториями точек фигуры при этом будут дуги окружностей с центром в центре вращения, а их векторы скоростей по модулю пропорциональны расстояниям до центра вращенияR (радиусам вращения):

V =   R, (3.7)

где  – угловая скорость вращения плоской фигуры. Направлен вектор скорости в сторону вращения плоской фигуры по касательной к дуге окружности, описываемой точкой фигуры, и, следовательно, он будет перпендикулярен радиусу вращения.

Непоступательное движение плоской фигуры в своей плоскости, если у нее нет закрепленных точек, является плоским движением.

При определении скоростей точек плоской фигуры целесообразно использовать теорему о проекциях скоростей двух точек твердого тела: проекции скоростей двух точек тела на прямую, соединяющую их, равны (рис. 3.4):

V_A cos = V_B cos. (3.8)

В вариантах задач ([1], табл. 3.2, усл. 0-3) задана угловая скорость кривошипа 1 (см. пример 3.1), в вариантах задач ([1], табл. 3.2, усл. 4-6) задан модуль вектора скорости ползуна (см. пример 3.2), в вариантах задач ([1], табл. 3.2, усл. 7-9) задана угловая скорость кривошипа 4 (см. пример 3.3).

При определении скоростей точек и угловых скоростей звеньев механизма, совершающих плоское движение, необходимо выполнить следующие действия:

1) если для стержня, совершающего плоское движение, по условиям задачи необходимо определить его угловую скорость, то следует найти положение мгновенного центра скоростей одним из вышеизложенных способов, предварительно определив направления векторов скоростей его двух точек;

2) определить расстояние от точки стержня, скорость которой известна или ее можно предварительно определить, до мгновенного центра скоростей;

3) определить угловую скорость стержня в данный момент времени по формуле (3.6);

4) зная угловую скорость стержня, определить по формуле (3.5) искомые скорости его точек;

5) если угловую скорость стержня определять по условиям задачи не нужно и известна скорость какой-либо точки или ее можно предварительно определить, то для определения скорости точки, у которой известно направление вектора скорости, целесообразно воспользоваться теоремой о проекциях скоростей двух точек тела (3.8).

Пример 3.1. Плоский многозвенный механизм образован стержнями O₁A = l₁= 0,4 м, AD = l₂ = 1,2 м, EB = l₃ = 1,4 м, O₂E = l₄ = = 0,8 м и ползуном В, соединенными друг с другом и неподвижными опорами О₁ и О₂ шарнирами (рис. 3.5).

Кривошип O₁А вращается с постоянной угловой скоростью ₁ = 1,5 рад/c. Точка D находится посередине стержня ВЕ.

Определить для заданного положения механизма скорости V_B, V_E, V_D точек B, E, D и угловые скорости ₃ и ₄ стержней BE и О₂Е.

Решение. Кривошипы О₁А и О₂Е совершают вращательное движение вокруг неподвижных точек О₁ и О₂ соответственно, стержни AD и ЕВ - плоскопараллельное движение, ползун В – поступательное движение по горизонтальной направляющей.

Вычислим модуль скорости точки А кривошипа O₁A по формуле (3.7):

м/с.

Векторскорости точкиА перпендикулярен O₁A и направлен в сторону вращения кривошипа (кривошип вращается против хода часовой стрелки).

Определим направление вектора скорости точкиD стержня AD. С этой целью построим мгновенный центр скоростей для стержня ВЕ, к которому также принадлежит точка D (рис. 3.6). Мгновенный центр скоростей (точка Р) лежит на пересечении перпендикуляров направлениям скоростей точек В и Е, восстановленных в этих точках. Векторы скоростей иточекВ и Е

направлены вдоль горизонтальной направляющей и вдоль стержня ВЕ соответственно. Соединим точки D и Р. Вектор скорости точки D составляет прямой угол с прямой DP. Направим его так, чтобы его проекция и проекция вектора на прямуюAD были одного знака.

Определим косинус угла , который составляет вектор скорости точкиD с прямой AD. С этой целью определим сторону РЕ прямоугольного треугольника ВРЕ (рис. 3.6):

РЕ =

Рассмотрим далее прямоугольный треугольник PDЕ. По теореме Пифагора определим гипотенузу PD:

PD = .

Применим теорему синусов для треугольника BPD (рис. 3.6):

, или

Применив к стержню AD теорему о проекциях скоростей двух его точек, определим скорость точки D: .

Откуда 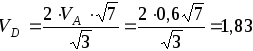м/с.

Зная положение мгновенного центра скоростей для стержня ЕВ, определим его угловую скорость по формуле (3.6):

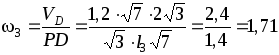рад/с.

По формуле (3.5) определим модули скоростей точек В и Е:

м/с,

, где м.

Следовательно, V_E = 1,71  0,81 = 1,39 м/c.

Зная скорость точкиЕ, определим угловую скорость кривошипа О₂Е по формуле (3.7):

м/с.

Пример 3.2. Пусть теперь при тех же условиях вместо угловой скорости ₁ кривошипа O₁A задан модуль вектора скорости ползуна V_B = = 5 м/с, направленного от точки В к b (рис. 3.7).

Определить для заданного положения механизма скоростиV_E, V_D, V_A точек Е, D, А и угловые скорости ₁, ₂, ₃, ₄ стержней О₁А, AD, BE и О₂Е.

Решение. Определим направление вектора точкиЕ. Он составляет прямой угол с прямой О₂Е и направлен так, чтобы его проекция и проекция вектора скорости ползуна на прямуюВЕ были одного знака. По теореме о проекциях скоро-стей двух точек тела (3.8):

V_E = V_В cos60 = 2,5 м/с.

Вычислим угловую ско-рость ₄ кривошипа О₂Е по формуле (3.7):

рад/с.

Угловую скорость ₃ стержня ВЕ определим по формуле (3.5), построив мгновенный центр скоростей для стержня ВЕ (пример 3.1):

, где ВР = 1,62 м.

Следовательно, рад/с.

Зная угловую скорость стержня ВЕ, определим скорость V_D точки D по формуле (3.5):

V_D = ₃  PD = 3,09  l₃= 3,09 1,4  = 3,3 м/с.

Применив к стержню AD теорему о проекциях скоростей двух его точек, определим скорость точки А:

, где cos = (пример 3.1).

Следовательно, м/с.

Вычислим угловую скорость ₁ кривошипа О₁А по формуле (3.5):

рад/с.

Для определения угловой скорости ₂ построим мгновенный центр скоростей стержня AD, который лежит на пересечении перпендикуляров направлениям скоростей и, восстановленных в этих точках (точкаР₁, рис. 3.7). В прямоугольном треугольнике P₁AD определим косинус острого угла (90 – ) при катете AD: cos (90 – ) = , гдеsin (90 –) = = sin 30(пример 3.1).

Следовательно, cos (90-) =

Определим угловую скорость ₂ стержня AD по формуле (3.6):

где из прямоугольного треугольника м и, следовательно,рад/с.

Пример 3.3. Многозвенный механизм (рис. 3.8) приводится в движение кривошипом , вращающимся в данный момент времени с угловой скоростьюрад/с. Длины стержней даны в примере 3.1. Определить для заданного положения механизма скоростииточекВ и А и угловую скорость стержняDA. Определить также ускорение точки А, если угловое ускорение стержня в заданный момент времени имеет значениерад/с.

Решение. Вычислим модуль скорости точки Е кривошипа по формуле (3.7):

м/с.

Пусть кривошип вращается по ходу часовой стрелки. Вектор скорости перпендикулярен стержнюи направлен в сторону его вращения. СкоростьточкиВ определим с помощью теоремы о проекциях скоростей двух точек тела (3.8), применив ее к стержню ЕВ:

и, следовательно, м/с.

Для определения направления вектора скороститочкиD построим мгновенный центр Р₃ скоростей для стержня ВЕ, которому принадлежит точка D. Точка Р₃ лежит на пересечении перпендикуляров направлениям скоростей и, восстановленных в этих точках (рис. 3.8). Соединим точкиР₃ и D. Так как прямая Р₃D делит по условиям задачи сторону ВЕ равнобедренного треугольника Р₃ВЕ пополам, то прямая Р₃D является также высотой треугольника и вектор скорости точкиD будет направлен вдоль стержня ВЕ перпендикулярно высоте Р₃D, которая является для точки D радиусом вращения вокруг мгновенного центра скоростей Р₃.

Величину вектора скоро-сти определим по теореме о проекциях скоростей двух точек стержняВЕ (3.8):

.

Откуда м/с.

Проведем из точек иD вспомогательные горизонтальные линии и. Так как в равнобедренном треугольникеугол при вершинеС равен , то угол=и, следовательно,=. Тогда векторсоставляет с направлениемDА угол, равный Вектор скороститочкиА, как принадлежащий кривошипу , перпендикулярен ему и направлен в сторону его вращения.

Зная углы, которые составляют векторы скорости ис направлением стержняDА по теореме о проекциях скоростей двух точек тела (3.8), определим величину скорости точкиА:

.

Откуда

м/с.

Для вычисления угловой скорости стержняDА нужно определить его мгновенный центр скоростей Р₂. Точка Р₂ лежит на пересечении перпендикуляров направлениям векторов и, восстановленных в точкахD и А. Угол при вершине D треугольника Р₂DА равен Тогда угол при вершинеР₂ равен и, следовательно, треугольник является равнобедренным. ТогдаАР₂ = DА =

= 1,2 м.

По формуле (3.6)

1,82 рад/с.

Угловую скорость кривошипа определим по формуле (3.7)

5,45 рад/с.

Тогда ускорение точки А по формуле (3.4) равно

12,05 м/с².

Ответ: = 1,6 м/с,= 2,18 м/с,= 1,82 рад/с,12,05 м/с².