
Свободные затухающие колебания
Пружинный маятник:
![]() .
.
![]() ,
где
- параметр (коэффициент) затухания,
,
где
- параметр (коэффициент) затухания,
![]() .
.
Математический маятник:
![]() .
.
Решение уравнения свободных затухающих колебаний:
Предположим, что
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.
![]()
![]() ,
,
![]() .
Отсюда
.
Отсюда
![]() .
Обозначив
.
Обозначив
![]() ,
получим:
,
получим:
![]() - решение уравнения свободных затухающих
колебаний.
- решение уравнения свободных затухающих
колебаний.
Если трение мало
![]() ,
то
,
то
![]() .
.
Основные характеристики затухающих колебаний.
В ремя
релаксации – время, в течение которого
значение параметра убывает в e
раз:
ремя
релаксации – время, в течение которого
значение параметра убывает в e
раз:
![]()
![]() .
.
Декремент затухания
характеризует, во сколько раз амплитуда
колебаний убывает за один период:
![]() .
.
Логарифмический декремент
затухания характеризует, во сколько
раз изменяется логарифм убывания
амплитуды:
![]() .
.
Пусть
![]() и совершается N
колебаний, т.е.
и совершается N
колебаний, т.е.
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.
Скорость и ускорение
затухающих колебаний:
![]() ,
,
![]() ,
,
![]() .
.
Добротность системы
![]() .
.
Э нергия
нергия
![]() ,
,
![]() .
.
![]() .
При
.
При
![]()
![]() .
.
Вынужденные колебания
Д ля
пружинного маятника:
ля
пружинного маятника:
![]() ,
где m
– масса тела, F
– амплитуда силы,
- циклическая частота
силы.
,
где m
– масса тела, F
– амплитуда силы,
- циклическая частота
силы.
Для математического маятника:
![]() .
.
Длительность переходного режима совпадает со временем релаксации.
![]() - амплитудно-частотная характеристика
вынужденных колебаний,
- амплитудно-частотная характеристика
вынужденных колебаний,
![]() - фазо-частотная характеристика
вынужденных колебаний.
- фазо-частотная характеристика
вынужденных колебаний.
Общее уравнение:
![]() ,
где первое слагаемое представляет собой
начальное колебаний системы, которое
из-за затухания постепенно сходит на
нет, а второе – установившийся режим
вынужденных колебаний.
,
где первое слагаемое представляет собой
начальное колебаний системы, которое
из-за затухания постепенно сходит на
нет, а второе – установившийся режим
вынужденных колебаний.
Резонанс.
Н айдём
максимум амплитуды колебаний в зависимости
от частоты воздействующей силы. Для
этого решим уравнение
айдём
максимум амплитуды колебаний в зависимости
от частоты воздействующей силы. Для
этого решим уравнение
![]() .
Получим:
.
Получим:
![]() .
.
Резонанс – явление резкого
возрастания (убывания) амплитуды
вынужденных колебаний при стремлении
частоты воздействия внешней силы к
частоте собственных колебаний (точнее,
к величине
![]() ,
где
- коэффициент затухания, но обычно
,
где
- коэффициент затухания, но обычно
![]() ).
).
Резонансная частота – частота внешней возбуждающей силы, при которой достигается максимум амплитуды вынужденных колебаний.
Наложение колебаний
Сложение колебаний одного направления
Пусть![]() ,
,
![]() .
Тогда
.
Тогда
![]() .
.
Векторная диаграмма:
![]() ,
,
![]() ,
,
![]() .
Тогда
.
Тогда
![]()
 ,
,
![]() .
.
Таким образом,
![]()
![]() .
.
Б иения:
Рассмотри два колебания:
иения:
Рассмотри два колебания:
![]() и
и
![]() ,
где
,
где
![]() .
Результирующее колебания будет
описываться уравнением
.
Результирующее колебания будет
описываться уравнением
![]() .
.
Частота биения:
![]() ,
период
,
период
![]() .
.
Взаимно перпендикулярные колебания
Рассмотрим два колебания,
происходящие во взаимно перпендикулярных
направлениях:
![]() ,
,
![]() .
.
-
Если
 и
и
 ,
то график
,
то график
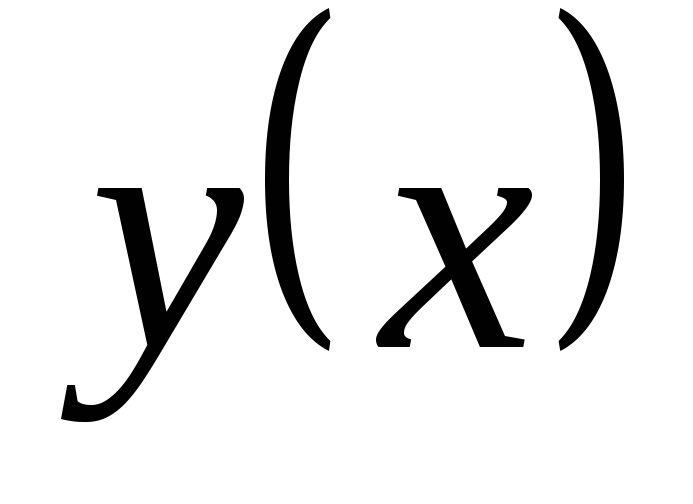 представляет собой прямую, проходящую
через начало координат.
представляет собой прямую, проходящую
через начало координат. -
Если
 ,
,
 и
и
 ,
то график
,
то график
 представляет собой эллипс, полуоси
которого равны A
и B.
представляет собой эллипс, полуоси
которого равны A
и B. -
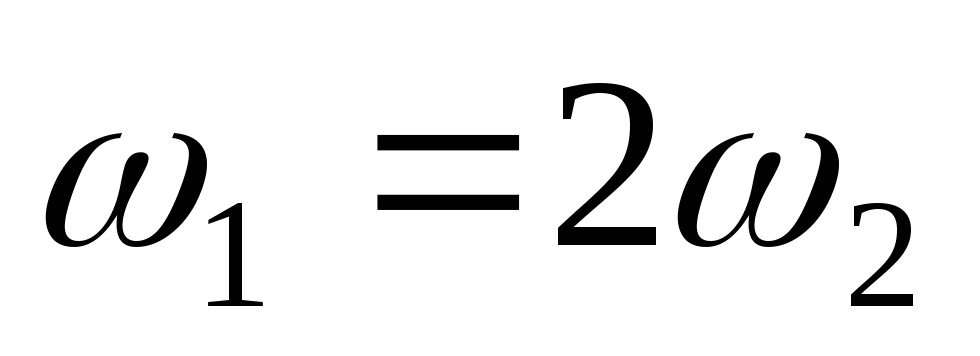 ,
,
 - график
- график
 представляет собой параболу.
представляет собой параболу. -
Общий случай:
 ,
,
 .
.
Фигура Лиссажу - эта линия, которую описывает тело, одновременно колеблющееся в двух взаимно перпендикулярных направлениях.
Свойства фигур Лиссажу:
-
Если колебания происходят с амплитудами A и B, то фигуру Лиссажу можно вписать в прямоугольник со сторонами
 и
и
 .
. -
Если
 - величина рациональная, то фигура
Лиссажу замкнута, иначе – незамкнута.
- величина рациональная, то фигура
Лиссажу замкнута, иначе – незамкнута. -
Отношение частот колебаний в горизонтальном и вертикальном направлениях равно отношению числа касаний фигуры вертикальных и горизонтальных сторон.
Механические волны
Распространение волн в упругой среде
Волны – процесс распространения колебаний в пространстве с течением времени.
Упругие волны – волны, распространяющиеся в упругой среде.
Волновая поверхность – геометрическое место точек среды, колеблющихся в одной фазе.
Волновой фронт – поверхность, разделяющая возмущённую и невозмущённую части среды.
Виды волн:
-
Поперечные – колебания в которых происходят поперёк направления распространения.
-
Продольные – колебания в которых происходят вдоль направления распространения.
В газообразной и жидкой среде колеблется плотность или, что то же, давление. В твёрдой среде и на границе раздела фаз – деформация или, что то же, механическое напряжение.
Волновое уравнение
И сследуем
колебания струны. Пусть в какой-то момент
времени струна деформирована так, как
показано на рисунке. Тогда уравнение
движения для этой струны выглядит так:
сследуем
колебания струны. Пусть в какой-то момент
времени струна деформирована так, как
показано на рисунке. Тогда уравнение
движения для этой струны выглядит так:
![]() .
Т.к.
.
Т.к.
![]() и
и
![]() ,
то
,
то
![]() .
Спроектируем это уравнение на ось :
.
Спроектируем это уравнение на ось :
![]() и на ось z:
и на ось z:
![]() .
Т.к.
.
Т.к.
![]() и
и
![]() очень малы, то
очень малы, то
![]() ,
,
![]() .
Тогда
.
Тогда
![]() .
Введём линейную плотность
.
Введём линейную плотность
![]() ,
тогда
,
тогда
![]() .
Таким образом мы получили волновое
уравнение поперечной волны:
.
Таким образом мы получили волновое
уравнение поперечной волны:
![]() ,
где
,
где
![]() .
.
Волновое уравнение для
продольной волны выглядит так:
![]() ,
где
,
где
![]() ,
p
– давление в среде распространения
волны.
,
p
– давление в среде распространения
волны.
Анализ механических волн
Пусть
![]() .
Тогда
.
Тогда
![]() ,
,
![]() и
и
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() .
Подставим это в волновое уравнение:
.
Подставим это в волновое уравнение:
![]()
 .
.
Общее решение волнового
уравнения:
![]() ,
где
,
где
![]() и
и
![]() - произвольные функции.
- произвольные функции.
Гармоническое решение
волнового уравнения:
![]() .
.
Период волны
![]() ,
фаза волны
,
фаза волны
![]() .
.
![]() - фазовая скорость волны.
- фазовая скорость волны.
Длина волны – расстояние,
на которое распространяется волна за
один период,
![]()
Волновое число
![]() .
.
Волновой вектор:
![]() ,
,
![]() сонаправлен с направлением распространения
волны.
сонаправлен с направлением распространения
волны.
Фазовая скорость волны –
скорость, с которой движутся точки
волны, колеблющиеся в одной фазе.
![]() .
.
Геометрические свойства волн
Для трёхмерного случая
выражение
![]() ,
где
- это оператор Лапласа, в декартовой
системе координат
,
где
- это оператор Лапласа, в декартовой
системе координат
![]() .
.
Плоские, цилиндрические и сферические волны – волны, волновой фронт которых представляет собой соответственно плоскость, цилиндр и сферу.
В случае плоской волны в
волновом уравнении достаточно заменить
![]() ,
т.е.
,
т.е.
![]() .
.
Для цилиндрической волны
![]() или, для гармонических колебаний,
или, для гармонических колебаний,
![]() .
Здесь
.
Здесь
![]() - проекция волнового вектора на ось
- проекция волнового вектора на ось
![]() .
.
Уравнение сферической
волны:
![]() ,
,
![]() .
Здесь
.
Здесь
![]() - проекция волнового вектора на
радиус-вектор.
- проекция волнового вектора на
радиус-вектор.
Бегущие и стоячие волны
Если
![]() ,
то направление распространения волны
сонаправленно с осью z.
Если же
,
то направление распространения волны
сонаправленно с осью z.
Если же
![]() ,
то направление распространения волны
противоположно направлено оси z.
,
то направление распространения волны
противоположно направлено оси z.
Рассмотрим сложение двух
одинаковых волн, двигающихся навстречу
друг другу. Т.е. пусть
![]() ,
,
![]() .
Тогда
.
Тогда
![]() - уравнение стоячей волны.
- уравнение стоячей волны.
Узлы – это точки, амплитуда
колебаний которых равна 0 (т.е.
![]() ).
).
Пучности – это точки,
амплитуда колебаний которых максимальна
(т.е.
![]() ).
).
Длина стоячей волны
![]() .
.
Граничные условия для стоячих волн:
-
Пусть струна закреплена с обеих сторон. Тогда
 и
и
 ,
где L
– длина струны, откуда
,
где L
– длина струны, откуда
 и
и
 ,
т.е.
,
т.е.
 или
или
 .
. -
Пусть теперь струна закреплена с одной стороны. Тогда
 и
и
 ,
откуда
,
откуда

 и
и
 .
. -
Наконец, пусть струна не закреплена ни на одном конце. Тогда
 и
и
 ,
откуда
,
откуда
 и
и
 .
.
Стоячие волны возбуждаются на струне или в акустической трубе только при соблюдении одного из этих условий.
Основной тон – колебание
с максимальной длиной волны:
![]() .
Остальные колебания называются
обертонами.
.
Остальные колебания называются
обертонами.
