уравнивания

Параметрический способ уравнивания геодезических сетей

Оценка точности

среднюю квадратическую ошибку непосредственно измеренных величин определяют по формуле

,

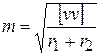где r₁ , r₂ – число условных уравнений в первой и второй группах, [vv] = [v’v’] + [v”v”] .

 

Параметрический способ уравнивания геодезических сетей имеет широкое применение, так как одинаковая структура приведенных к линейному виду уравнений поправок дает возможность составлять универсальные программы уравнивания на ЭВМ триангуляции, трилатерации, линейно-угловых, комбинированных и других построений. Как и в коррелатном способе, задача уравнивания решается под условием [pv²] = min.

В параметрическом способе сначала вычисляют координаты всех определяемых пунктов. Затем, используя эти координаты, с высокой точностью решают по всем сторонам обратные геодезические задачи и определяют длины и дирекционные углы сторон. После этого составляют уравнения поправок для всех непосредственно измеренных величин: горизонтальных направлений, измеренных расстояний, азимутов, придавая каждой измеренной величине вес p = c/m² .

От уравнений поправок переходят к нормальным уравнениям, число которых равно удвоенному числу определяемых пунктов. Из решения находят поправки в приближенные координаты определяемых пунктов, т.е. уравненные координаты пунктов. Выполняют вычисления окончательных длин сторон и дирекционных углов по уравненным координатам. Делают оценку точности уравненных элементов сети.

Одним из наиболее ответственных этапов уравнивания является установление точного соотношения весов всех измеренных в сети величин. Приняв в формуле веса p = c/m² и , где m_N – с.к.о. измеренного направления, получим

,

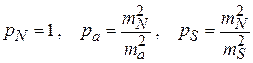где p_a , m_a , p_S , m_S – вес .к.о. азимута а и длины стороны s соответственно. При этом с.к.о. m должны быть получены не по внутренней сходимости результатов измерений, а по свободным членам соответствующих условных уравнений или другими способами, учитывающими случайные и систематические ошибки. В сетях триангуляции mопределяют по формуле Ферреро с использованием невязок ω большого числа n треугольников:

.

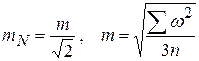двухгрупповой метод

При уравнивании больших сетей триангуляции возникает много условных и нормальных уравнений, что приводит к трудоемким вычислениям. Для уменьшения объема вычислений Крюгер предложил двухгрупповой метод, в котором условные уравнения делят на две группы, решают уравнения первой группы, находят первичные поправки v’ . Затем преобразуют уравнения второй группы и в результате их решения получают поправки v” и окончательные поправки v = v’+v”, такие же, что и при совместном решении уравнений.

Н.А. Урмаев предложил включать в первую группу все условные уравнения фигур неперекрывающихся треугольников. При этом нормальные уравнения первой группы принимают вид

,

а вычисление поправок 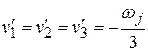сводится к распределению невязок треугольников с обратным знаком поровну на три угла.

По исправленным первичным поправками углам в каждом треугольнике вычисляют свободные члены условных уравнений второй группы и преобразованные коэффициенты

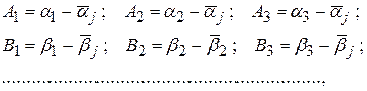
где 

Контроль: [A] = [B] = … = 0 .

Решив нормальные уравнения второй группы, находят коррелаты, позволяющие вычислить вторичные поправки v”, которые вводят в предварительно уравненные углы.

Коррелатный метод

Уравнивание триангуляции коррелатным способом.

Уравнивание коррелатным способом выполняют по углам или – более строго – по направлениям. Условные уравнения разделяют на угловые и синусные. Угловыми называют линейные условия, имеющие коэффициенты ±1 и 0. Синусными называют нелинейные условные уравнения, в которых содержатся синусы. В триангуляции после устранения невязок угловых условий дирекционный угол любой стороны сети определяется однозначно независимо от пути его передачи от исходных дирекционных углов.

В триангуляции имеются следующие виды угловых условий.

Условия фигур возникают в треугольниках и многоугольниках. В плоском треугольнике (рис.1а),

1 + 2 + 3 – 180⁰ = ω

где 1, 2, 3 – измеренные значения углов треугольника; ω – невязка в треугольнике. При уравнивании к углам J определяют поправки (J) и получают

1+ (1) + 2 + (2) + 3 + (3) – 180⁰ = 0.

 

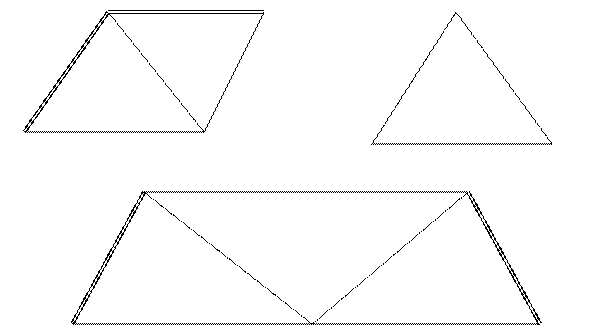
Рис.1

Из сравнения этих выражений находят условие фигур

(1) + (2) + (3) + ω = 0.

При уравнивании направлений для треугольника условное уравнение фигур имеет вид (рис1.б)

-(1) + (2) – (3) + (4) – (5) + (6) + ω = 0 ,

где ω = [2-1] + {4-3] + [6-5] – 180⁰.

Условия горизонта возникают на пунктах, на которых в уравнивание включены все углы, образуемые смежными направлениями, сумма этих углов равна 360⁰, т.е.

(1) + (2) + …+(N) + ω = 0.

При уравнивании по направлениям условий горизонта не возникает.

Условия исходных дирекционных углов возникают при вставке цепочки треугольников в угол или между исходными сторонами и состоят в том, что сумма уравненных углов должна равняться величине жесткого угла или дирекционный угол стороны СД (рис.1.в) должен равняться его вычисленному значению от исходного дирекционного угла стороны АВ с использованием уравненных значений углов треугольников.

На рис.1.а α_ВС + 6 + 3 – α_ВА = ω.

После введения поправок и преобразований получаем условное уравнение

(3) + (6) + ω = 0 .

Для сети на рис.1.в.

α_АВ ± 180⁰ – С₁ ± 180⁰ + С₂ ± 180⁰ – С₃ – α_СД = ω . (1)

После введения поправок и преобразований находим условное уравнение

– (С₁) + (С₂ ) – (С₃ ) + ω = 0 .

Если дирекционные углы α_АВ и α_СД (рис.1.в) получены из измерений и поправки (α_АВ) и (α_СД) в их значениях определяют из уравнивания сети, то условное уравнение дирекционных углов в этом случае имеет вид

 

– (С₁) + (С₂ ) – (С₃ ) + (α_АВ) - (α_СД) + ω = 0 ,

где ω определяют по формуле (1).

Синусные условия состоят из полюсных, базисных и координатных; их учет необходим для однозначного определения длины любой стороны сети независимо от пути ее определения от исходных сторон. Координатные условия обеспечивают однозначное получение координат любого пункта сети.

Полюсные условия возникают в центральных системах и геодезических четырехугольниках, так как в этих фигурах одна сторона является избыточной. На рис.2 с учетом замены отношения сторон отношением синусов противолежащих им углов имеем