Mat_Metody_Otvety

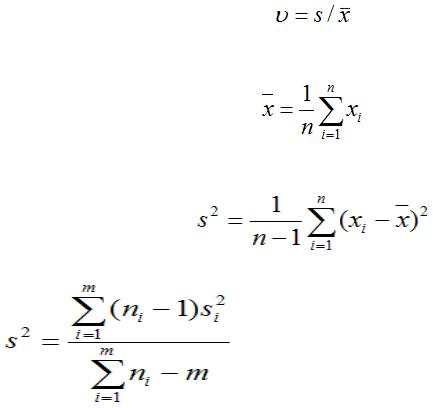
Непрерывная случайная величина может принимать любое значение в некотором конечном или бесконечном интервале. При испытаниях часто получают выборку значений непрерывной случайной величины с некоторым распределением вероятности получения того или иного значения. Точнее, реальные распределения в большинстве случаев достаточно близки к нормальному.

Основные параметры нормального распределения – математическое ожидание М случайной величины и еѐ генеральное среднеквадратическое отклонение (СКО) σ (или генеральная дисперсия σ2). Математическое ожидание - это центр группировки результатов испытаний, при отсутствии систематических погрешностей соответствует количественной характеристике объекта испытаний. Дисперсия (или СКО) – мера рассеяния результатов испытаний. Найти их значения абсолютно точно невозможно. Однако при объѐме выборки n не менее 25…30 обычно считают, что точечные оценки параметров нормального распределения с приемлемой точностью равны параметрам. Кроме того, можно достаточно точно рассчитать генеральную дисперсию при проведении серий испытаний, в которых генеральная дисперсия не меняется (вычисление дисперсии по текущим измерениям), например, при приѐмо-сдаточных испытаниях.

Применяется также мера рассеяния, называемая коэффициентом вариации. Генеральный коэффициент вариации

γ=σ/M; (1.1)

Выборочный коэффициент вариации

Точечной оценкой математического ожидания М является среднее значение выборки 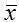(В Excel функция СРЗНАЧ):

Точечной оценкой генеральной дисперсии является выборочная несмещенная дисперсия (функция ДИСП):

По текущим измерениям дисперсия может быть вычислена по формуле

Здесь ni – объем испытаний (объѐм выборки) в каждой серии, si2 – дисперсии в соответствующих сериях, m – количество серий.

Оценка генерального СКО - выборочное СКО (функция СТАНДОТКЛОН):

Точечные оценки малоинформативны, поскольку являются случайными величинами и могут значительно отличаться от оцениваемого параметра. Для повышения информативности используют интервальные оценки (рассчитывают доверительные интервалы). При достаточно точно известной генеральной дисперсии σ2) доверительный интервал для математического ожидания определяют из соотношения

(1.3)

или

Здесь уровень значимости α=1-Р (Р -доверительная вероятность), z1-α/2 – квантиль стандартного нормального распределения (функция НОРМСТОБР), n – объѐм испытаний (объѐм выборки). Если генеральная дисперсия неизвестна, доверительный интервал для математического ожидания определяют из соотношения

Здесь tα;k – коэффициент Стьюдента (СТЬЮДРАСПОБР), k=n-1 – число степеней свободы. Доверительный интервал для дисперсии определяют из соотношения:

Здесь χ2 - критерий распределения хи-квадрат (функция ХИ2ОБР), k=n-1 – число степеней свободы. Извлекая из всех частей неравенства квадратный корень, можно получить интервальную оценку СКО.

КРИТЕРИЙ ЗНАЧИМОСТИ

— правило проверки статистических гипотез, основанное на свойствах распределения меры отклонения эмпирической функции распределения выборки при одной гипотезе от эмпирической функции распределения при др. гипотезе. Эта мера определяется разл. способами (см. Критерий χ2, Критерий Стъюдента и др.). При выяснении согласия между распределениями выборки и теоретическим пользуются термином — критерий согласия. Распределение выборки не может точно совпадать с гипотетическим распределением, но это отклонение может быть вызвано случайными колебаниями или быть значимо, т. е. указывать на наличие действительного различия между неизвестным распределением совокупности и

гипотетическим. Если мы вычисляем меру D отклонения выборочного распределения от гипотетического и по выборочному распределению D, а также заранее заданному уровню значимости а находим такое число Do, что P(D > D0) =

α, ςо такое отклонение значимо,	т. е.	при	данном уровне	значимости
а гипотеза отвергается. Если же P(D	≤ D0)	=	α, ςо подобная	проверка не

опровергает гипотезы. Значение а определяется практическими соображениями. При решении геол. задач обычно за величину а принято 0,05, что нельзя считать достаточно обоснованным.

Корреляция определяет степень, с которой значения двух переменных «пропорциональны» друг другу. Пропорциональность означает просто линейную зависимость. Корреляция высокая, если на графике зависимость «можно представить» прямой линией (с положительным или отрицательным углом наклона). Таким образом, это простейшая регрессионная модель, описывающая зависимость одной переменной от одного фактора.

В производственных условиях обычно информации, полученной из диаграмм рассеяния при условии их корректного построения, бывает достаточно для того, чтобы оценить степень зависимости у от х. Но в ряде случаев требуется дать количественную оценку степени связи между величинамих и у. Такой оценкой является коэффициент корреляции.

Отметим основные характеристики этого показателя.

Он может принимать значения от –1 до +1. Знак «+» означает, что связь прямая (когда значения одной переменной возрастают, значения другой переменной также возрастают), «–» означает, что связь обратная.

Чем ближе коэффициент к |1|, тем теснее линейная связь. При величине коэффициента корреляции менее 0,3 связь оценивается как слабая, от 0,31 до 0,5 – умеренная, от 0,51 до 0,7 – значительная, от 0,71 до 0,9 – тесная, 0,91 и выше – очень тесная.

Если все значения переменных увеличить (уменьшить) на одно и то же число или в одно

ито же число раз, то величина коэффициента корреляции не изменится.

При r=±1 корреляционная связь представляет линейную функциональную зависимость. При этом все наблюдаемые значения располагаются на общей прямой. Еѐ ещѐ называют линией регрессии.

При r=0 линейная корреляционная связь отсутствует. При этом групповые средние переменных совпадают с их общими средними, а линии регрессии параллельны осям координат.

Равенство r=0 говорит лишь об отсутствии линейной корреляционной зависимости

(некоррелированности переменных), но не вообще об отсутствии корреляционной, а тем более, статистической зависимости.

Основываясь на коэффициентах корреляции, вы не можете строго доказать причинной зависимости между переменными, однако можете определить ложные корреляции, т.е. корреляции, которые обусловлены влияниями «других», остающихся вне вашего поля зрения переменных. Лучше всего понять ложные корреляции на простом примере. Известно, что существует корреляция между ущербом, причиненным пожаром, и числом пожарных, тушивших пожар. Однако эта корреляция ничего не говорит о том, насколько уменьшатся потери, если будет вызвано меньше число пожарных. Причина в том, что имеется третья переменная (начальный размер пожара), которая влияет как на причинѐнный ущерб, так и на число вызванных пожарных. Если вы будете учитывать эту переменную, например, рассматривать только пожары определѐнной величины, то исходная корреляция между ущербом и числом пожарных либо исчезнет, либо, возможно, даже изменит свой знак. Основная проблема ложной корреляции состоит в том, что вы не знаете, кто является еѐ носителем. Тем не менее, если вы знаете, где искать, то можно воспользоваться частные корреляции, чтобы контролировать (частично исключѐнное) влияние определѐнных переменных.

Корреляция, совпадение или необычное явление сами по себе ничего не доказывают, но они могут привлечь внимание к отдельным вопросам и привести к дополнительному исследованию. Хотя корреляция прямо не указывает на причинную связь, она может служить ключом к разгадке причин. При благоприятных условиях на еѐ основе можно сформулировать гипотезы, проверяемые экспериментально, когда возможен контроль других влияний, помимо тех немногочисленных, которые подлежат исследованию.

Иногда вывод об отсутствии корреляции важнее наличия сильной корреляции. Нулевая корреляция двух переменных может свидетельствовать о том, что никакого влияния одной переменной на другую не существует, при условии, что мы доверяем результатам измерений.

Регрессионный анализ		— статистический		метод исследования		влияния одной или
	́
нескольких независимых		переменных		на зависимую		переменную .

Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных, а не причинно-следственные отношения.

Корреля́ция (взаимосвязь) - статистическая взаимосвязь двух или нескольких случайных величин. При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин. Математической мерой корреляции двух случайных величин служит корреляционное отношение 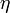, либо коэффициент корреляци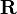и (или 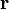). В случае, если изменение одной случайной величины не ведѐт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.

Впервые в научный оборот термин «корреляция» ввѐл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века.

Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными. В первом случае предполагается, что мы можем определить только наличие или отсутствие связи, а во втором — также и еѐ направление. Если предполагается, что на значениях переменных задано отношение строгого порядка, тоотрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой. При этом коэффициент корреляции будет отрицательным. Положительная корреляция в таких условиях — это такая связь, при которой увеличение одной переменной связано с увеличением другой переменной. Возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин.

Погрешности средств измерений

По способу определения различают погрешности средств измерений:

абсолютную,

относительную

приведенную.

Погрешности средств измерений зависят от внешних условий и

подразделяются на основные и дополнительные.

Основной погрешностью называют погрешность, которая определена в нормальных для данного средства измерений условиях. Параметры нормальных условий указываются в паспорте каждого прибора.

Дополнительные погрешности возникают при отклонении влияющих величин от нормальных значений. Они могут быть учтены при помощи так называемых коэффициентов влияния, если известна функция влияния, то есть зависимость поправочного коэффициента от разности между действительным и нормальным значениями данного влияющего параметра.

По характеру проявления при повторных измерениях погрешности средств измерения подразделяются на

систематические;

случайные.

Систематическими называются

-погрешности средств измерения, не изменяющиеся с течением времени и

»либо являющиеся постоянными величинами, например, неточность установки нуля;

»либо функциями определенных параметров, например, погрешность градуировки; большинство дополнительных погрешностей

Систематические погрешности остаются постоянными по знаку и величине при повторных измерениях. Поэтому их присутствие чрезвычайно трудно обнаружить.

Систематические погрешности внешне никак себя не проявляют и могут долгое время оставаться незамеченными. Единственный способ их обнаружения состоит в периодической поверке измерительных приборов по образцовым мерам или сигналам.

Систематические погрешности характеризуются определѐнной закономерностью, поэтому в случае обнаружения они могут быть устранены введением соответствующих поправок

Случайными называются погрешности средств измерения, изменяющиеся случайным образом. Такие погрешности не могут быть предсказаны ни по знаку, ни по величине, и исключить их введением поправок невозможно.

Однако присутствие случайных погрешностей легко обнаружить при многократных измерениях одной и той же величины в одинаковых условиях. Наличие случайной погрешности приводит к некоторому разбросу полученных результатов. Величина случайной погрешности при этом рассчитывается на основании методов математической статистики и теории вероятностей.

Аддитивные

и

мультипликативные

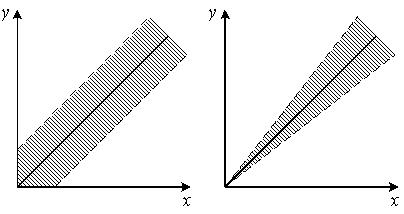
погрешности. Аддитивной

погрешностью называется погрешность, постоянная в каждой точке шкалы. Мультипликативной погрешностью называется погрешность, линейно возрастающая или

убывающая с ростом измеряемой величины.

Различать аддитивные и мультипликативные погрешности легче всего по полосе погрешностей.

Если абсолютная погрешность не зависит от значения измеряемой величины, то полоса определяется аддитивной погрешностью. Иногда аддитивную погрешность называют погрешностью нуля.

			а	б
Если постоянной величиной является относительная погрешность, то полоса погрешностей
меняется в	пределах	диапазона	измерений	и погрешность называется мультипликативной
(рис.2.2, б).
Ярким	примером аддитивной погрешности является погрешность квантования
(оцифровки).
Класс	точности	измерений	зависит от	вида погрешностей. Рассмотрим класс точности

измерений 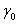для аддитивной и мультипликативной погрешностей: - для аддитивной погрешности:

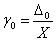, где 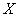- верхний предел шкалы, 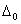- абсолютная аддитивная погрешность. - для мультипликативной погрешности

.

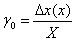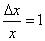- это условие определяет порог чувствительности прибора (измерений).

Абсолютная величина погрешности для обоих типов погрешностей может быть выражена одной формулой:

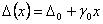, где - аддитивная погрешность, 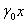-мультипликативная погрешность. Относительная погрешность с учетом (2.1.1) выражается формулой

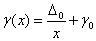, и, при уменьшении измеряемой величины, возрастает до бесконечности. Приведенное значение погрешности

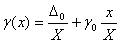возрастает с увеличением измеряемой величины.

Класс точности – это числовая характеристика, нормативно устанавливающая предельное гарантированное значение погрешности для средств измерений данного типа.

Согласно действующему стандарту, класс точности указывается одним из чисел следующего ряда:

(1; 1.5; 2; 2.5; 4; 5; 6) 10k,

где k – показатель степени, который может быть любым (положительным или отрицательным) целым числом.

Класс точности — основная метрологическая характеристика прибора, определяющая допустимые значения основных и дополнительных погрешностей, влияющих на точность измерения.

Погрешность может нормироваться, в частности, по отношению к:

результату измерения (по относительной погрешности)

вэтом случае, по ГОСТ 8.401-80 (взамен ГОСТ 13600-68), цифровое

обозначение класса точности (в процентах) заключается в кружок.

длине (верхнему пределу) шкалы прибора (по приведенной погрешности) Для стрелочных приборов принято указывать класс точности,

записываемый в виде числа, например, 0,05 или 4,0. Это число дает максимально возможную погрешность прибора, выраженную в процентах от наибольшего значения величины, измеряемой в данном диапазоне работы прибора. Так, для вольтметра, работающего в диапазоне измерений 0 — 30 В, класс точности 1,0

определяет, что указанная погрешность при положении стрелки в любом месте шкалы не превышает 0,3 В. Соответственно, среднее квадратичное отклонение s прибора составляет 0,1 В.

Относительная погрешность результата, полученного с помощью указанного вольтметра, зависит от значения измеряемого напряжения, становясь недопустимо высокой для малых напряжений. При измерении напряжения 0,5 В погрешность составит 60 %. Как следствие, такой прибор не годится для исследования процессов, в которых напряжение меняется на 0,1 — 0,5 В.

Обычно цена наименьшего деления шкалы стрелочного прибора согласована с погрешностью самого прибора. Если класс точности используемого прибора неизвестен, за погрешность s прибора всегда принимают половину цены его наименьшего деления. Понятно, что при считывании показаний со шкалы нецелесообразно стараться определить доли деления, так как результат измерения от этого не станет точнее.

Следует иметь в виду, что понятие класса точности встречается в различных областях техники. Так в станкостроении имеется понятие класса точности металлорежущего станка, класса точности электроэрозионных станков

(по ГОСТ 20551).

Обозначения класса точности могут иметь вид заглавных букв латинского алфавита, римских цифр и арабских цифр с добавлением условных знаков. Если класс точности обозначается латинскими буквами, то класс точности определяется пределами абсолютной погрешности. Если класс точности обозначается арабскими цифрами без условных знаков, то класс точности определяется пределами приведѐнной погрешности и в качестве нормирующего значения используется

наибольший по модулю из пределов измерений. Если класс точности обозначается арабскими цифрами с галочкой, то класс точности определяется пределами приведѐнной погрешности, но в качестве нормирующего значения используется длина шкалы. Если класс точности обозначается римскими цифрами, то класс точности определяется пределами относительной погрешности.

Аппараты с классом точности 0,5 (0,2) начинают работать в классе от 5 % загрузки. а 0,5s (0,2s) уже с 1 % загрузки

Косвенным называется измерение, при котором значение измеряемой величины находят путем расчета по известной зависимости на основании результатов прямых измерений всех параметров, входящих в эту зависимость.

Например:

определение плотности вещества по массе и объему образца;

определение плотности газа известного состава на основании прямого измерения температуры газа.

определение расхода воздуха или газа по средней скорости потока и площади сечения канала.

Совокупные измерения – это одновременные измерения нескольких одноимѐнных величин, при которых искомые значения величин находят решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин.

Пример: массы отдельных гирь набора определяются по известной массе одной из них и по результатам

прямых сравнений масс различных сочетаний гирь. Совместные измерения – это производимые

одновременно измерения нескольких неодноимѐнных величин для нахождения зависимости между ними, либо с целью поиска оптимальных условий.

Пример: определение зависимости плотности жидкости от температуры:

производят измерения температуры (например, термометром),

проиводят измерения плотности (например, ареометром) при этих температурах,