Критерий устойчивости Михайлова

Возьмем характеристический многочлен линейной системы n-го порядка

с положительными коэффициентами (необходимое условие устойчивости). Подставив в него чисто мнимое значение  = j; получим

,

Изобразим годограф этого выражения на комплексной плоскости X(), Y(), изменяя  от нуля до бесконечности .

Практически годограф строится по точкам. Задают несколько разных значений  в интервале между 0 и  (достаточно по одной точке в каждом квадранте) и по формулам вычисляют координаты точек кривой Михайлова X(), Y().

Эти годографы называются кривыми Михайлова. Они имеют для различных n примерно такие формы, как показано на рисунке.

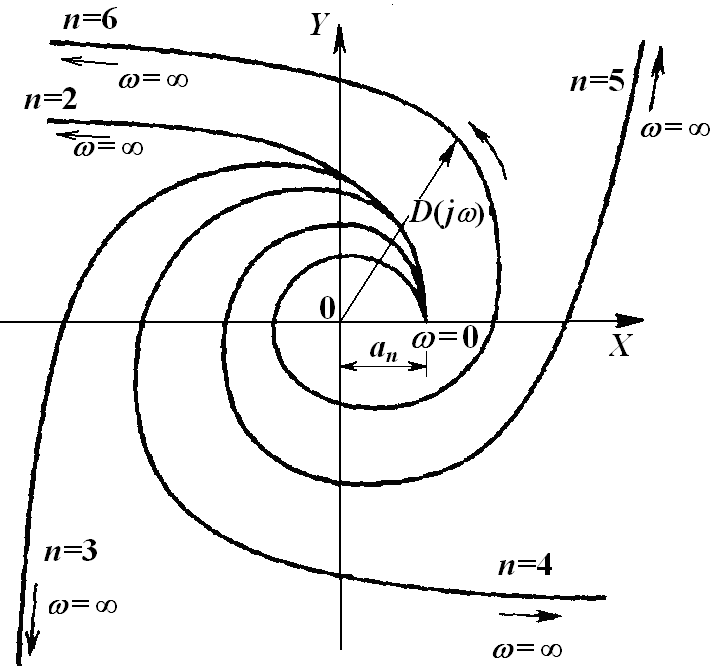
Заметим следующее: при  = 0 имеем X = a_n, Y = 0; при  =  будет X = +  или X = – , а Y = +  или Y = – .

Предельные значения +  или –  зависят от показателя степени n.

Если все a_i положительны, то для n=3 при  = 0 будет X = – , Y = – ; а для n=5 получим X = + , Y = +  и т. д.

Определение критерия Михайлова

Для устойчивости линейной системы n-го порядка необходимо и достаточно, чтобы изменение аргумента функции D(j) при изменении частоты  от 0 до  равнялось бы n/2:

argD(j) = n/2     при 0    .

Другими словами

Для устойчивости линейной системы n-го порядка необходимо и достаточно, чтобы кривая Михайлова проходила последовательно n квадрантов против часовой стрелки (все время окружая начало координат).

Определение границ устойчивости по критерию Михайлова.

Границы устойчивости можно объединить равенством ₁ = j₀, включая  = 0.

Если характеристическое уравнение системы D() = 0 имеет корень ₁ = j₀, то

X(₀) = 0,    Y(₀) = 0.

Графически это означает попадание одной точки кривой Михайлова  = ₀ в начало координат, как показано на рисунках:

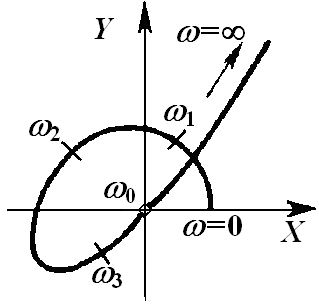
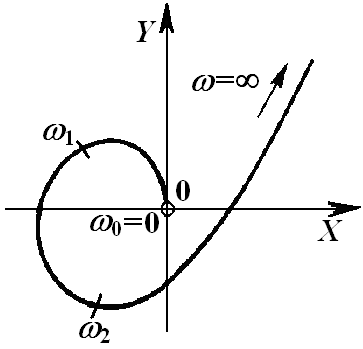
Физический смысл величины  = ₀ – частота колебаний системы на границе устойчивости.

На границе устойчивости системы все остальные корни, кроме  = j₀, должны лежать слева от мнимой оси плоскости. Иначе система будет неустойчивой. Поэтому требуется, чтобы кривая Михайлова проходила бы все остальные квадранты, кроме пропущенного из-за прохождения через начало координат, как показано, например, для n=5, на рис. б.

Следовательно, например, годограф на следующем рисунке соответствует не границе устойчивости, а неустойчивой системе.

Выражения для X и Y используются для построения областей устойчивости системы на плоскости любых двух параметров A и B, выбираемых при проектировании системы (например, коэффициент усиления и постоянная времени).

На границе устойчивости имеем:

X(₀,  A,  B) = 0,    Y(₀,  A,  B) = 0,

причем параметры A и B входят в коэффициенты характеристического уравнения системы. Путем задания разных значений величины ₀ (0    ) из этих уравнений определяются значения параметров A и B. В результате по точкам строятся границы устойчивости на плоскости A, B.

Пример. Рассмотрим определение границ и области устойчивости системы по критерию Михайлова для простого случая. Пусть характеристическое ураввнение будет:

Тогда для D(j) = X() + j Y() получим выражения для действительной и мнимой частей:

, .

Для устойчивости системы третьего порядка необходимо, чтобы кривая Михайлова проходить последовательно через три квадранты против часовой стрелки, все время окружая начало координат при изменении частоты от 0 до , т.е. ₀₁<₀₂<₀₃

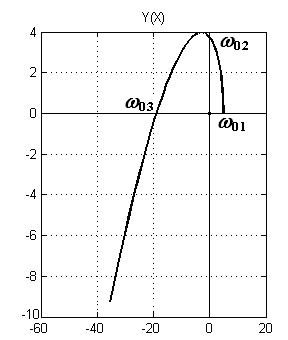
Приравняем мнимую часть нулю:

Y() =  –Т₁Т₂³ = 0, или Y() =  (1–Т₁Т₂²)=0.

Отсюда получим ₀₁=0, ₀₃²=1/(Т₁Т₂).

Приравняем действительную часть нулю: X() = K–(Т₁+Т₂)²=0. 

Отсюда получим ₀₂²= K/(Т₁+Т₂)

Так как ₀₁<₀₂<₀₃, то получим 0 < K/(Т₁+Т₂) < 1/(Т₁Т₂)

или K > 0, K < (Т₁+Т₂)/Т₁Т₂,

0 <K < (1/Т₁+1/Т₂).

Границы устойчивости:

1) ₀₁²=₀₂², K=0.

2) ₀₂²=₀₃², K_гр=(Т₁+Т₂)/(Т₁Т₂)=1/Т₁+1/Т₂.

По критерию Михайлова удобно определять области устойчивости для систем любого порядка. Достоинством критерия Михайлова является то, что он проще и нагляднее для определения устойчивости системы, чем критерий Гурвица, особенно для систем высокого порядка.